Chapter 2 Introduction to Detailed Notes

These are notes that I made on my reading of the textbook. There is no real attempt to have comments on absolutely everything in the book noted here. At the same time, there is supplementary material here that is not in the book.

After writing out the notes for the first few sections, it has become clear that there is a tendency to make this a "teaching" document. As much as possible, efforts will be made to not do this. Rather, if there is teaching material to be presented then that will be done in separate pages, with pointers inserted here.

Chapter 2: Linear and Quadratic Functions

Chapter 2, Section 0: Solving Linear and Quadratic Equations

I am not happy with the start of chapter 2.

In version 1 only

In the first place the initial sentence is a circular definition of "solving".

In the second place, we mean different things when we say "solve this equation", depending upon the condition of the equation. Third, the text launches into solving a linear equation, 6x–5y–15=0, but really solving it to find the intercepts. This is a specialized version of solving equations, one that requires an explanation of why we convert a varaible to a constant, at least on a temporary basis.

In version 1 only

And fourth, the solution does not find the intercepts, but rather the non-zero coordinates of the intercepts.

Let me propose an alternate start:

We often talk about "solving and equation". Unfortunately, we do not always mean the same thing when we say this. In general, if we have an equation that has just one variable, such as x, then "solving the equation" means finding the set of all values that can be substituted for the one variable to produce a valid equation. Thus, to solve 4x – 5 + 7x = 9x + 11 we simplify the equation until we obtain x = 3 which tells us that the set of values that can be substituted for x in the original problem to give a true statement is exactly the set {3}. Likewise, to solve |x – 5| = 13 means finding that both elements of the solution set {18, –8} can be substituted for x in the original equation to give a true statement. In the same way, for the problem x⁴ – 27x² + 14x + 120 = 0 can be solved to produce the solution set {4, 3, –2, –5} In all of these problems we have a single unknown variable. We solve the problem by finding the set of values that can be substituted for the variable to produce a true statement.

If there are two or more variables in an equation, then we can solve the equation "for a variable". We do this by isolating the particular variable on one side of the equation, allowing all other constants and expressions to stand on the other side of the equation. For example, we can solve

5x – 6y = 30 for either x or y. If we solve for x, then we isolate x on one side and we have x = (6y + 30) / 5 However, we could solve for y by isolating the y to get y = (–5x + 30)/(–6) Note that we could give that result in a slightly different form as y = (5x – 30)/(6) Either version is correct, but the second looks nicer in that it does not have the negative value in the denominator.

Notice that the equation

5x – 6y = 30 has a solution set. It is the set of points (x,y) that makes the equation true. As we will see later, and as you probably know now, there are an infinite number of elements in this solution set. It contains elements such as (6,0), (0,–5), (12,5), and (18,10). In also has elements (3,–2.5) and (20,11.6666666...). If we graph the solution set on the coordinate plane, the solution set for 5x – 6y = 30 is a straight line representing an infinite set of ordered pairs that form the solution set of the equation. A graph of that solution set is given as

Caution! Your browser is not supporting Java.

Again, these are the ordered pairs that can have their coordinates substituted into the original equation for x and y, respectively, to produce a true statement.

Although the equation

5x – 6y = 30 has an infinite solution set, there are two particular values that generally interest us. These are called the y–intercept and the x–intercept, the points on the graphed line where that line crosses the y–axis and the x–axis, respectively. Remember that all points on the y–axis have an abscissa equal to 0. Similarly, all points on the x–axis have an ordinate that is equal to 0. We can find the y–intercept for the equation 5x – 6y = 30 by setting the value of x to be 0, since we know that the abscissa for that point will be 0. That gives us 5(0) – 6y = 30
^–6y = 30
y = 30 / ^–6
y =^–5 which means that the y-intercept is the point (0,^–5).

In the same way, we can find the x–intercept, the point on the graph where the ordinate is zero, by setting y to be 0, and then solving the resulting equation (for x). In that case we have

5x – 6(0) = 30
5x = 30
x = 30 / 5
y = 6 which means that the x–intercept is the point (6,0).

On page 100, the solution for Example 2 gives the answer in two forms,

y =	^–6x + 15	and	y =	6	x – 3

	^–5			5

It is important to note that both are correct, but that the second version is preferred because it does not have an explicit negative value for the denominator.

Still on page 100, the text presents a TI-86 screen image for solving Example 3. It is important to note the steps needed to get to this image. See the Intro To Solver on the TI-86 page for a sequence of screen images. And still on page 100, the text presents a TI-89 screen image for solving Example 4. Those students using a TI-89 or TI-92 should look at the page Intro to Solver on the TI-89/92 for some details on using this feature.

In version 1 only

At the bottom of page 101, the last paragraph starts with the sentence "The easiest way to factor simple quadratics is to mentally multiply all of the possibilities." I am not sure what that says, much less what it means. I do know that for quadratics that have the form x² + bx + c = 0 we need to try to find the factors of c, and in particular, the factors that add (or subtract in some cases) to give the value b.

In version 1 only

The TI-86 solution given for Example 12 at the bottom of page 102 is incorrectly labelled as "Example 5".

In addition, the text ignores explaining the origin of that TI-86 screen. It is the result of using the "poly" key,

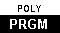, on the calculator. See the web page Intro to Poly on the TI-86 for a further explanation.

In version 1 only

Also, note that "challange" should be "challenge" in the paragraph at the bottom of page 102.

At the bottom of page 104, the TI-86 screen for Example 14 is the result of the "poly" key.

This is a point in the text where I want to show students the various "quad" programs for the TI-85 and TI-86. Students should look at the Quad program for the 85/86 as an introduction. The page Quadratic Formula Program, QUAD1, gives a refinement of the original QUAD program, but it does so for the TI-83. There are similar program refinements for the TI-85/86. Links to those programs are on the Quadratic Formula Program, QUAD1 page. Then, there is a further enhancement to the program that is outlined on the Quadratic Formula Program, QUAD2 page, again for the TI-83. Fortunateley, that page contains pointers to the corresponding versions of quad2 for the TI-85/86.

Chapter 2, Section 1: Linear Functions

Page 108, middle of the page. We say "...a line is fixed by connection two ordered pairs of the function"

In version 1 only

and yet, in Example 1, we use three ordered pairs of the function.

The book should say "...a line is fixed by connecting any two distinct ordered pairs of the function. However, it is advisable to locate three or more ordered pairs, points, before drawing the line. By doing this we are more likely to identify any errors in our work. (That is, if we locate three or more points and they are not on a straight line, then we know that we have an error in our calculations.)

The Figure at the bottom of the page has been augmented, "touched up", for this display.

Page 109, top paragraph. Change from "x-intercept (y=0)" to "x-intercept (where y=0)". Change from "y-intercept (x=0)" to "y-intercept (where x=0)".

Example 2: insert the word "by" before the word "locating".

In version 1 only

Page 110, last sentence, remove the word "for", and replace "changes" with "change".

Replae the first sentence on the top of page 113 with:

In the previous example, we were able to determine the equation of a line by examining a few ordered pairs of the relation. It is not usual to be able to just look at some ordered pairs and "see" the equation of the line.

In version 1 only

Replace the middle sentence on page 113 with: "By making this statement we restrict the possible pairs (x,y) to be those that satisfy the conditions of the line."

On page 116, insert the following above EXAMPLE 12:
Note that we have an equation for a vertical line, x=a, where a is some number. This has the more general form 1x + 0y = a The set of points on the line is represented as {(x,y)| 1x + 0y = a } Since it is a set of ordered pairs, this is a relation; however, it is not a function.

The graphs for Examples 14 and 15 on page 117 are really quite nice. We should show students how to produce such graphs. See the web page Shading on the TI-86 for the required steps.

For problems 15-18 on page 121, assume equal measures on the two axes.

Chapter 2, Section 2: Parallel, Perpendicular and Intersecting Lines

In version 1 only

Page 125: First paragraph, change the line that states "Conversely, if two lines have the same slope, they are parallel." to "Conversely, if two lines have the same slope then they are either parallel or they are the same line."

In version 1 only

Page 126: at the bottom, fourth line from the bottom. That line starts with a symbol,

, that we use to mean "therefore".

Page 127: the graph in the middle of the page. The two lines on that graph actually appear to be perpendicular. Note that all four of the graphs in the left column below are of the same lines, namely

y = (2/3)x – 2 and y = (-3/2)x + 3

Figure 2.1.1L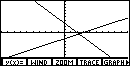	Figure 2.1.1R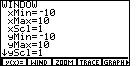
Figure 2.1.2L	Figure 2.1.2R
Figure 2.1.3L	Figure 2.1.3R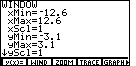
Figure 2.1.4L	Figure 2.1.4R

Clearly, Figures 2.1.1L and 2.1.3L do not even begin to look like perpendicular lines. The display presented here is not quite the same as an exact representation of the screen on the calculator. More than likely, on this web page, Figure 2.1.4L does not show the lines as being perpendicular, whereas Figure 2.1.2L does seem to have perpendicular lines. However, on the calculator, although both Figure 2.1.2L and 2.1.4L appear to have close to perpendicular lines, 2.1.4L appears to be a better representation. The screens in the right column above give the window settings for the corresponding graphs. Figure 2.1.1R shows the STANDARD setting, 2.1.2R shows the DECIMAL setting, 2.1.3R shows the modified setting, and 2.1.4R shows the effect of using the ZSQR zoom on the previous setting.

Page 129
This seems like a good place to introduce the standard form for linear equations and to use that form to give another view of equations for parallel and perpendicular lines. I will create a modest example for this on the stndform.htm web page.

In version 1 only

Page 133, in Exmple 9, part c solution, the left side of the equations should read f(x+h)-f(x).

Chapter 2, Section 3: Linear Regression

In version 1 only

Page 139, there is an extra space after the second word in the first sentence.

Insert the following to replace the part of the first paragraph following the two sets of ordered pairs.

Each ordered pair represents an event. The x-value is viewed as an input value, the values that we use to identify the event. The y-value is th outcome value, the result of finding the ordered pair. For the first set of ordered pairs above we have the second coordiante of each ordered pair is exactly twice the value of the first coordinate. We express this as y=2x. In the second set of ordered pairs the second coordinate is exactly equal to the square of the first coordinate. For that case we have y=x². For either example, if we know the rule, then we can predict with certainty the second coordinate as long as we know the first. That is, if we know the input value, the first coordinate, we can apply the rule and determine the output value, the second coordinate. For example, for the first set, if we know that the input value is 7, then we determine that the output value needs to be 14. This works well with our mathematical rules. However, in real life paired data may not be so precisely linked. Real data that is closely tied to a strict formula is said to be highly correlated. Data that is not closely tied to a strict rule is said to have a low correlation.

There should be some explanation of the steps needed to generate the graph at the bottom of page 139. Similar material is covered in the Math 181 course. In that course, however, the text presents Linear Regression in the context of a "use" for solving systems of linear equations. In this course we do not have the benefit of that background. Rather, we are looking at Linear Regression as a process that turns some everyday associations into a linear model of the relationship between two values. There are three web pages that were developed for the Math 181 course to help explain Linear Regression and to guide students through the use of the calculators to determine Linear Regression coefficients. The first page, Regression Example, explains the basic idea ofa linear regression. Unfortunately for this Math 179 course, some of the material on that page will not make much sense, because it is tuned to the Math 181 material. Then there are two pages to explain the process of doing a linear regression on the calculator, one page for the TI-85 and one for the TI-86. These pages should be use as an aid to understanding regression and to learning the steps needed to produce the graphs and equations in the Math 179 text. However, the actual steps to produce the graph on page 139, and the top graph on page 140, can be found on the page for Steps to a Linear Regression.

The graph and the text at the bottom of page 142 are worth some extra attention. The graph is there as a demonstration that not all relations are linear. The text asserts that the first three points seem to "fit" a line, however the fourth point (there is an error in the first version of the book where that last point is identified as the third point) "falls off". Actually "falls off" probably gives the wrong impression. That point is too high for the line through the first three points. It is more as if the fourth point "floats off" the expected path from the first three points. Then too, the last three points seem to fall on a line about as well as do the first three points. The text goes on to suggest that a different model, a quadratic or exponential model, might better fit the data. I have constructed a separate web page, othrreg.htm, to look at the data from example 3 on page 142 in more detail.

Chapter 2, Section 4: Quadratic Functions

In version 1 only

Replace the first line on page 146 with "Recall that the general polynomial function of degree n is expressed as".

In version 1 only

Replace the second sentence by "If we consider the case of a second degree polynomial, then we have the final three terms of the polynomial function above,".

In version 1 only

Replace the fragment by "This is the quadratic function."

In version 1 only

On page 147, it seems that we should remove the development of the quadratic formula from here and replace it with a reference to Chapter 2 section 0.

In version 1 only

Page 148, the last sentence in the middle paragraph should be rewritten as "A thorough understanding of the properties of quadratic functions is necessary to accomplish this goal. "

In version 1 only

On page 150, replace the sentence just before Example 5 with "In addition, as mentioned earlier, the x-intercepts are generally desirable points to locate to facilitate graphing."

In version 2 only

On page 149, replace the sentence just before Example 3 with "In addition, as mentioned earlier, the x-intercepts are generally desirable points to locate to facilitate graphing."

After finishing the presentation on page 157, the class developed a program, that they called ABC, to find all of the components given on page 157 based on the values of the coefficients, A, B, and C. That program is described and available for the TI-85 and TI-86 on the abcprog.htm web page.

On page 159, be aware that as you read the material, the equation at the top of the page is developed in the text that follows. You are not supposed to understand the development of that equation when it is first presented. Rather, continue reading to see the steps taken to arrive at the equation.

On page 160 we start the discussion of Quadratic Inequalities. I believe that we need to point out to students that we are constantly switching between one-variable quadratic inequalities and two variable quadratic equalities. That is, we look at a problem such as

x² + x – 2 < 0 and then we switch over to y = x² + x – 2 This distinction is important in that the previous part of the chapter we are really looking at the two-variable quadratic equality. If we were being consistent, then we should be looking at quadratic inequalities of the form y < x² + x – 2 What we are doing, however, is reverting to the one-variable case for the inequality and then we use the two-variable equality as a means to solve and understand the one-variable inequality.

Chapter 2, Section 5: Parametric Equations

Page 170, the second sentence in the second paragraph should read "The equations define functions of t, and can be graphed..."

I do not have other notes on the material in this section. However, there is a web page that demonstrates graphing parametric equations onthe TI-86. Note that the TI-85 is almost identical in operation, and that the TI-89 is not that much different (assuming that you already know how to graph functions with a TI-89). In other words, that web page is worth reading and studying. If there is sufficient interest, a similar page for the TI-89 (or even for the TI-83) will be constructed.