
# We want to use gnrnd4 so we need to load it
# into our environment
source("../gnrnd4.R")
# then use it to produce the values in Table 2
gnrnd4( key1=652179504, key2=0005300657 )
# then we will list all fo the values so that we
# can compare them to the ones in Table 2 just
# to be sure that we got the right values
L1
# then we can use the min() and max() functions to
# get the values for our range
min( L1 )
max( L1 )

In R we can use the min() function to find the
minimum value in the collection and the max()
function to find the maximum value in the collection.
We can get both of these same values via a different R function,
namely the summary() function, but we will present that
in the next section.
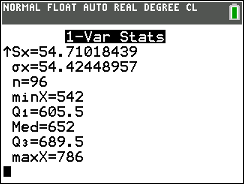
which clearly shows the value of Q1 as 605.5
and the value of Q3 as 689.5. (It is somewhat reassuring to
have the TI-83/84 also show us the same values for the minimum, 542,
the maximum, 786, and the median, 652, that we knew to
be correct.]
Alternatively, in our R session we could ask R to sort the values
just so that we can compare them to the values in Table 2-sorted. Then,
via the summary() function, we could get the output shown at the bottom of Figure 2.
First, here are the commands that we will use
# We want to see the sorted list of values
sort( L1 )
# We use the summary() function to get the Q1 and Q3 values
summary( L1 )

In Figure 2 we see that R gives us the same values for the minimum, median, and maximum. However, R shows the value 605.8 for Q1 and the value 689.2 for Q3. Different values than we found on the TI calculator, though not much different.
As was the case in our discussion of the median, this difference often disappears in
larger data collections where there a many repetitions of values in the collection.
In those situations, the "averaging" that shows up in some cases for finding
quartile points between data points ends up being the average of identical values.
The bottom line for us, in this course, is that we will use the
quartile values determined by the summary() command in R.
However, we should be a bit concerned because of the few decimal digits that are shown in the output
of the summary() command.
We notice that
the mean given by the summary() function is 652.2.
However, as we see in Figure 2a, R computes
and displays the mean with more significant digits
as 652.2188.

Clearly, the value shown in Figure 2 is a rounded one.
Therefore, we must assume that the values shown back in Figure 2 for
Q1 and Q3 are also rounded.
The question becomes,
"How do we get summary() to show more significant digits
of the computed values?" The answer to that is to
insert the command options(digits=9)
before we use
the summary() command. This is shown in Figure 2b,
along with a subsequent options(digits=7) command
that will reset R to the defaut number of digits.
Here are the commands we will use to generate Figure 2b:
# We can force summary to give an extra two digits
# by using the options() function before using summary()
options( digits=9 )
summary( L1 )
# And, then follow summary with another options()
# function to return our session to the default value of 7
options( digits=7 )
# And then we can repeat our summary() function just to
# demonstrate the return of the default setting
summary( L1 )

options() command gives R
an "idea" of the space to allocate, not a specific hard and fast rule.
quantile() function
as an alternative way to get Q1 and Q3.
We will use the command
# Let us look at two alternative ways fo find the quartiles.
# First, R has a command, quantile(), that we can use to find
# the 25th and 75th percentiles, which are the first and
# third quartiles.
quantile( L1, c( 0.25, 0.75 ))
# Using the quantile() function has the advantage of showing
# more significant digits than we had using the summary()
# function.

quantile() function shows more digits.
In fact it would show 7 if it needed that many.
long_summary() function.
This is a function that you should have in your directory of extra functions.
We can use the following commands to load and run long_summary().
# As noted in the text, there are different acceptable ways
# to compute Q1 and Q3. R uses one method, the TI-83/84
# calculators use a different method and therefore, at times,
# get Q1 and Q3 values that are different than what we
# get with R.
# It would be nice to see those alternative values. The
# function long_summary() will do this. However, we need to
# load long_summary() into our environment before we
# can use it.
source("../long_summary.R")
# Now that it is loaded we can use it
long_summary( L1 )
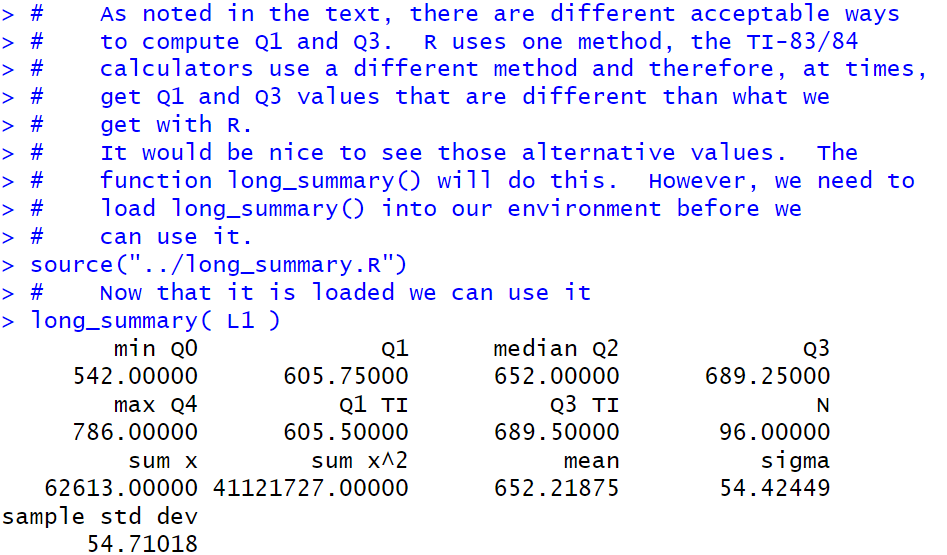
summary() command along with maany more values, including
the Q1 and Q3 values that we would get if we
had a TI-83/84 calculator do this work for us.
Furthermore, the long_summary() function produces values
with the full 7 digits of display (set by the default value that we restored way back in
Figure 2b.
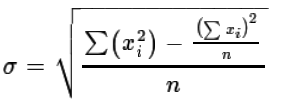 , for computing the
standard deviation.
, for computing the
standard deviation.
Of course, if we really wanted to, we could go through all of the steps needed to compute, in R, the standard deviation by following either of the two formulae. Such steps are really not worth it since R has a command, sd(), that would seem to do the computation for us. However, let us take just a few minutes to go through the process of evaluating each formula for our data just to see that they not only give us the same answer but also that the built-in R function produces that same value. We will use the data in Table 2 for this.
First, let us evaluate `sigma = sqrt((sum_(i=1)^n ( x_i-mu)^2)/n)`. The steps to do this, or at least to do the start of this, are shown in Figure 3. Note that in most cases I have chosen to show the computed values immediately after the computation, but such a display is just meant to help in confirming what is going on. It is not at all required for the actual determination of the standard deviation.
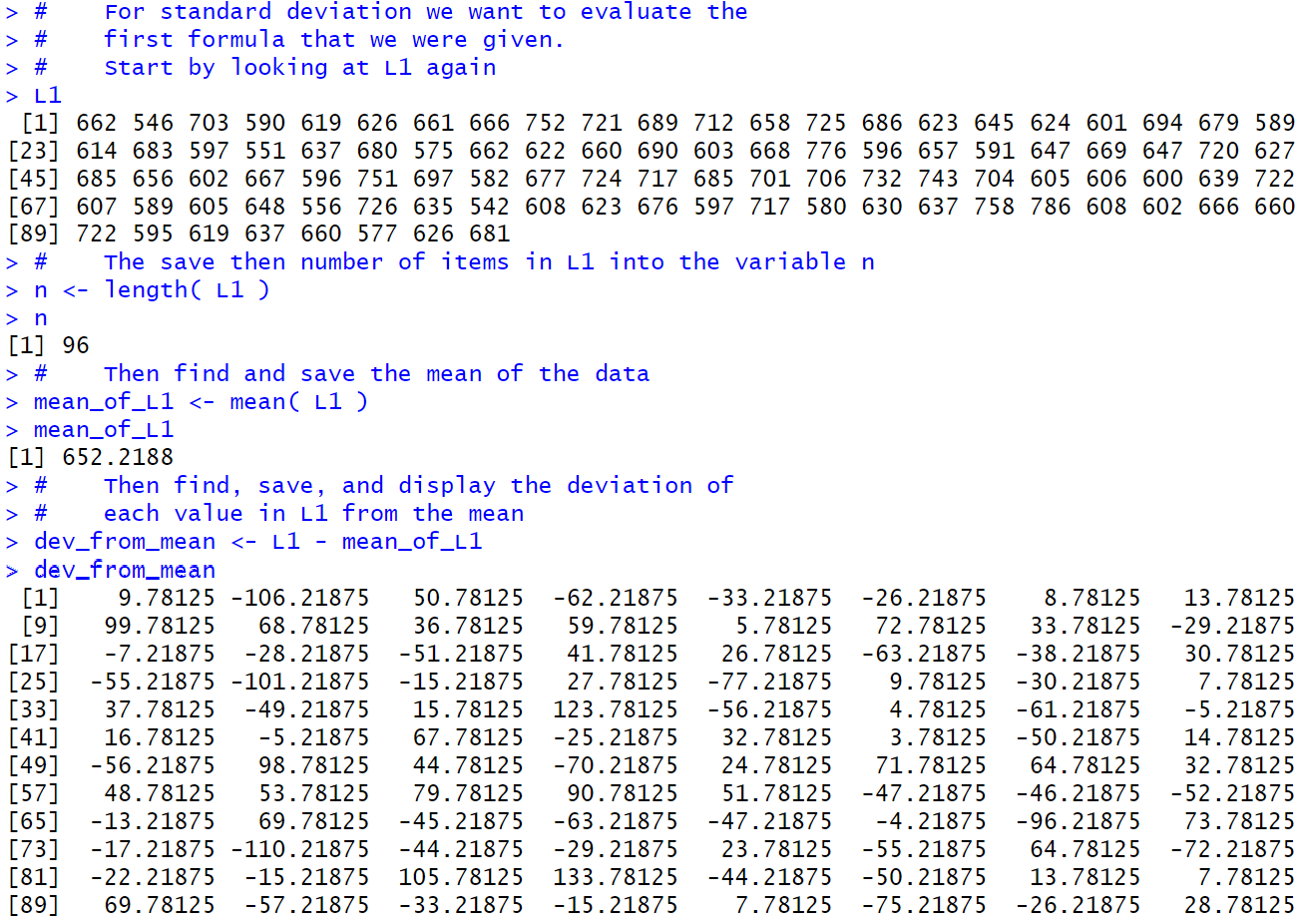
We start by showing the contents of L1.
After that we put the length of L1 into the variable n.
Once we have that we can compute the mean of the data which we store in
mean_of_L1.
Now that we have the mean we can compute the deviation from the mean
for each value in L1. We store all 95 of these values in
dev_from_mean and the display of those values, when compared to the values in L1
should convince you that that is exactly what happened.
Here are the commands we will use:
# For standard deviation we want to evaluate the
# first formula that we were given.
# Start by looking at L1 again
L1
# The save then number of items in L1 into the variable n
n <- length( L1 )
n
# Then find and save the mean of the data
mean_of_L1 <- mean( L1 )
mean_of_L1
# Then find, save, and display the deviation of
# each value in L1 from the mean
dev_from_mean <- L1 - mean_of_L1
dev_from_mean
Then we can continue the process in Figure 4.
There our first step is to get the square of
each of those deviations from the mean.
We put those 95 values into sq_of_dev, and again display the
results just for our own benefit.
Just below halfway in Figure 4 we find the
sum of the squared deviations from the mean
and store that in sum_sq_dev.
We move from there to find the
mean squared deviations from the mean
and store that into
mean_sum_sq_dev.
Finally, we compute the root mean squared deviations from the mean
and store this in root_mean_ssd. This is the standard deviation.
Here are the commands we will use:
# Now find all the squares of those deviations
sq_of_dev <- dev_from_mean^2
sq_of_dev
# the find, store, and display the sum of the squared deviations
sum_sq_dev <- sum( sq_of_dev )
sum_sq_dev
# divide that sum by the number of items to get the mean
mean_sum_sq_dev <- sum_sq_dev / n
mean_sum_sq_dev
# Finally, take the square root of that mean
root_mean_ssd <- sqrt( mean_sum_sq_dev )
root_mean_ssd
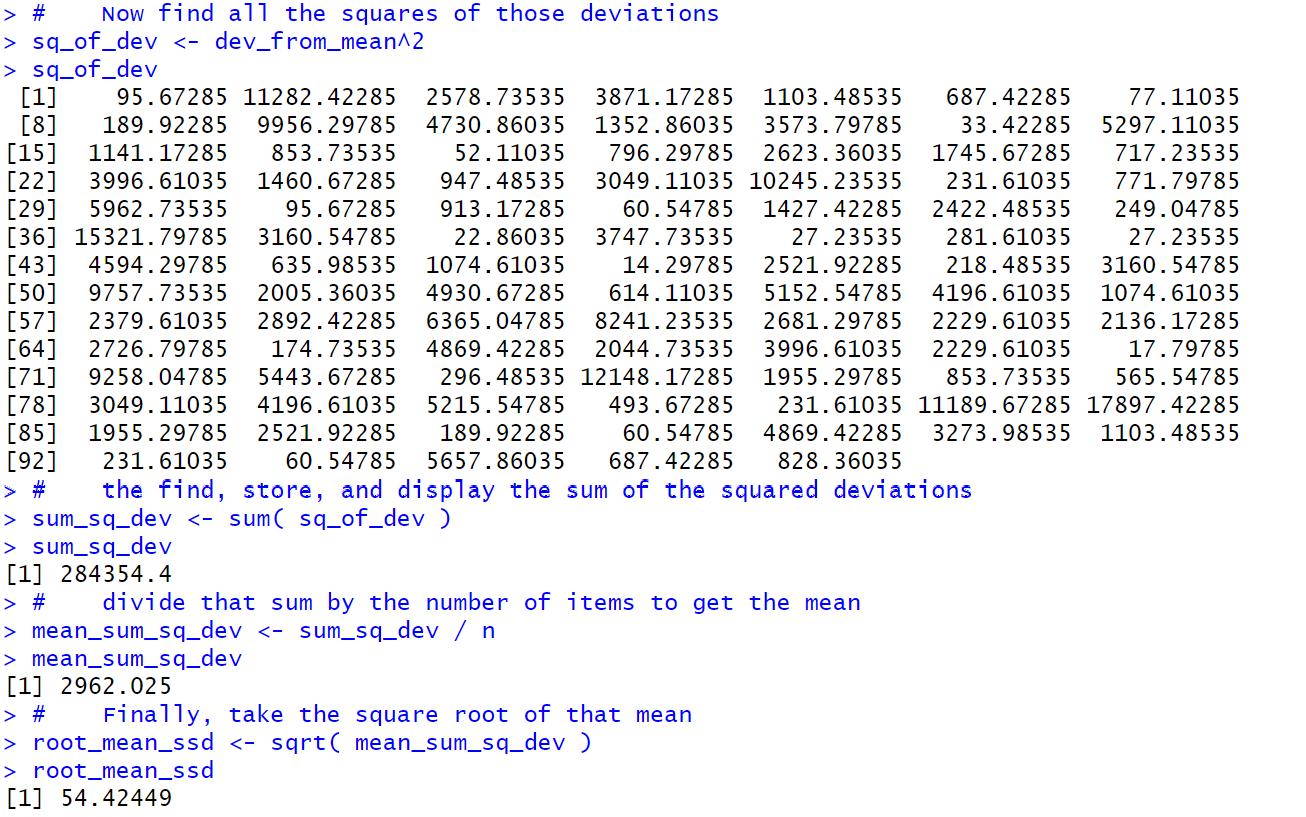
Thus, using the basic definition of standard deviation we get the value 54.42449.
Let us do the computation using
the alternative formula: `sigma = sqrt( ("sumsqx" - ("sumx")^2/n)/n)`.
We start, in Figure 5, by restating the value of n.
After that we get the sum of the values
and store that in sum_x.
Then we compute the sum of the squares of the values
and store that in sumsq_x.
At that point we are ready to just compute
the standard deviation
which turns out to be exactly the same value,
54.42449.
Here are the commands we will use:
# Now find the standard deviation using the alternative formula
# Just for clarity, recompute and display the length of L1
n <- length( L1 )
n
# Then get and display the sum of the x values, the values in L1
sum_x <- sum( L1 )
sum_x
# Then get and display the sum of the squares of the x values
sumsq_x <- sum( L1^2 )
sumsq_x
# The we have all we need to evaluate the formula
stdev <- sqrt( ( sumsq_x -sum_x^2/n) / n )
stdev

It is somewhat comforting to see that we get the same result
using either formula and that, as advertised, the second formula is
easier to compute than is the first.
You might also note that the output for the long_summary()
function included the values for the sum of the values and the sum of the squared values.
We now turn our attention to the R built-in function
sd(), which looks like it should yield the
standard deviation. At the top of
Figure 6 we ask for sd(L1) and we
get the answer 54.71018, which is close, but not the same
as the two answers that we got before.

What is wrong? Where did we make a mistake?
The problem is that the sd() function in R computes the standard deviation for a sample and all of the work that we have done has been to find the sample deviation for a population. At this point in the course we have yet to talk about the difference between a sample and a population. It looks like we need to at least introduce that distinction here so that we can move forward. The standard deviation for a sample, usually called `s_x`, is given by the defining formula:

Relief! We got the same answer, 54.42449, that we computed above.
Of course, making that adjustment in R whenever we want to
get the standard deviation of a population is not
convenient at all.
A better solution is for us to construct our own function that will
take care of this for us.
You have been given such a function, called pop_sd(), in
the file called pop_sd.R. We can load that file into our
environment via the source("../pop_sd.R") command as shown in Figure 7.

Now that the function is in the environment we can just go ahead and use it, as shown in Figure 8.

We get exactly the result that we
expect.
Although this is not a programming course, a look at the function
pop_sd() shows us that it is doing just what we
would do by hand. It finds the length of the list of values and then takes the
standard deviation for a sample, sd(), and multiplies it
by the square root of (n-1)/n. Here is a listing of the lines of the function:
pop_sd<-function( input_list )
{ n <- length( input_list)
sd( input_list )*sqrt((n-1)/n)
}
It is important to remember to use sd() to find the standard deviation of a sample
and to use pop_sd() to find the standard deviation of a population (and remember that
sd() is a built-in function,
but pop_sd() must be loaded into your environment).
long_summary() function,
back in Figure 2d.
# We want to use gnrnd4 so we need to load it
# into our environment
source("../gnrnd4.R")
# then use it to produce the values in Table 2
gnrnd4( key1=652179504, key2=0005300657 )
# then we will list all fo the values so that we
# can compare them to the ones in Table 2 just
# to be sure that we got the right values
L1
# then we can use the min() and max() functions to
# get the values for our range
min( L1 )
max( L1 )
# We want to see the sorted list of values
sort( L1 )
# We use the summary() function to get the Q1 and Q3 values
summary( L1 )
# Compare the "mean" shown in summary with the result
# of mean()
mean(L1)
# We can force summary to give an extra two digits
# by using the options() function before using summary()
options( digits=9 )
summary( L1 )
# And, then follow summary with another options()
# function to return our session to the default value of 7
options( digits=7 )
# And then we can repeat our summary() function just to
# demonstrate the return of the default setting
summary( L1 )
# Let us look at two alternative ways fo find the quartiles.
# First, R has a command, quantile(), that we can use to find
# the 25th and 75th percentiles, which are the first and
# third quartiles.
quantile( L1, c( 0.25, 0.75 ))
# Using the quantile() function has the advantage of showing
# more significant digits than we had using the summary()
# function.
# As noted in the text, there are different acceptable ways
# to compute Q1 and Q3. R uses one method, the TI-83/84
# calculators use a different method and therefore, at times,
# get Q1 and Q3 values that are different than what we
# get with R.
# It would be nice to see those alternative values. The
# function long_summary() will do this. However, we need to
# load long_summary() into our environment before we
# can use it.
source("../long_summary.R")
# Now that it is loaded we can use it
long_summary( L1 )
# For standard deviation we want to evaluate the
# first formula that we were given.
# Start by looking at L1 again
L1
# The save then number of items in L1 into the variable n
n <- length( L1 )
n
# Then find and save the mean of the data
mean_of_L1 <- mean( L1 )
mean_of_L1
# Then find, save, and display the deviation of
# each value in L1 from the mean
dev_from_mean <- L1 - mean_of_L1
dev_from_mean
# Now find all the squares of those deviations
sq_of_dev <- dev_from_mean^2
sq_of_dev
# the find, store, and display the sum of the squared deviations
sum_sq_dev <- sum( sq_of_dev )
sum_sq_dev
# divide that sum by the number of items to get the mean
mean_sum_sq_dev <- sum_sq_dev / n
mean_sum_sq_dev
# Finally, take the square root of that mean
root_mean_ssd <- sqrt( mean_sum_sq_dev )
root_mean_ssd
# Now find the standard deviation using the alternative formula
# Just for clarity, recompute and display the length of L1
n <- length( L1 )
n
# Then get and display the sum of the x values, the values in L1
sum_x <- sum( L1 )
sum_x
# Then get and display the sum of the squares of the x values
sumsq_x <- sum( L1^2 )
sumsq_x
# The we have all we need to evaluate the formula
stdev <- sqrt( ( sumsq_x -sum_x^2/n) / n )
stdev
# now use the built-in function
sd(L1)
# we could convert this to the standard deviation
# for a population by multiplying by sqrt((n-1)/n)
sd(L1)*sqrt((n-1)/n)
# or we could codify that in a new function
source("../pop_sd.R")
pop_sd( L1 )
©Roger M. Palay
Saline, MI 48176 October, 2015