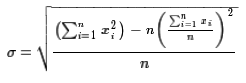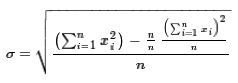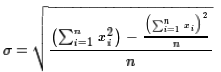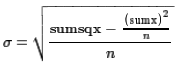Standard Deviation Formula
Return to Measures of Dispersion
The defining formual for the standard deviation of a collection of
n data values, 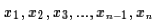 is given by
is given by
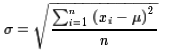 Although this is the defining formula, it is a pain to actually use because you need to
find the mean, μ, first and then go through the data and find the squared
differences between each point and μ, and then get the sum of those values, which you
then divide by the number of values, n, and finally take the square root of the answer.
Although this is the defining formula, it is a pain to actually use because you need to
find the mean, μ, first and then go through the data and find the squared
differences between each point and μ, and then get the sum of those values, which you
then divide by the number of values, n, and finally take the square root of the answer.
Fortunately, we can use some math to reconfigure the formual into a more convenient
version. We start this with a rewrite where we expand the squared difference,
much as we learned in Algebra I that
(a – b>²=a² – 2ab + b²)
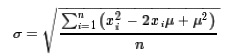 But that sum can be broken apart to be the separate sums of the three terms
But that sum can be broken apart to be the separate sums of the three terms
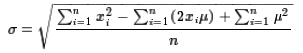 However the term
However the term  ,
so we could rewrite the formula as
,
so we could rewrite the formula as
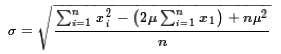 ,
Now, with a little slight of hand,
we can make this a bit more complex in order to be able to actually simplify it later.
We can rewrite
,
Now, with a little slight of hand,
we can make this a bit more complex in order to be able to actually simplify it later.
We can rewrite
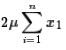 as
as
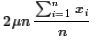 , but that has the factor
, but that has the factor
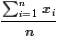 which is our definition of μ.
Therefore,
we can replace
which is our definition of μ.
Therefore,
we can replace 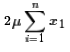 with
with
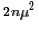 and our formula becomes
and our formula becomes
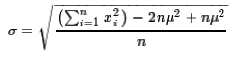 Of course this reduces to
Of course this reduces to
 Then, replacing
Then, replacing 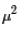 with
with 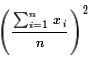 we get
we get
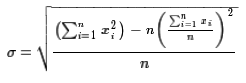 but that simplifies to
but that simplifies to
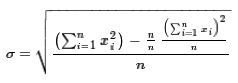 Finally, we can rewrite this as
Finally, we can rewrite this as
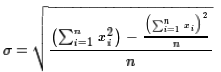 That final formula may look terrible, but, computationally, it is wonderful.
It says that to find the standard deviation
we need to
know the number of values, n, and the sum of the xi values
which we could call sumx and the sum of the xi²
values which we could call sumsqx. Then the formula becomes
That final formula may look terrible, but, computationally, it is wonderful.
It says that to find the standard deviation
we need to
know the number of values, n, and the sum of the xi values
which we could call sumx and the sum of the xi²
values which we could call sumsqx. Then the formula becomes
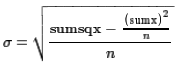 This is the formula that small, and even some larger, calculators
use because, as you are entering data values the calculator
takes the value that you enter, adds it to the running total sumx,
adds the square of the value to the running total sumsqx
and increase the count of the data values, n, by one.
Then, whenever you ask for the standard deviation
the calculator just has to do the last formula above.
The system has the extra advantage that if you realize that somewhere in the data entry
process you made a mistake in entering a data value then it is easy to delete that value.
You hit some button to tell the calculator to remove a value and all it has to do
is ask for the value, subtract it from sumx,
subtract its square from sumsqx, and decrease the number of data items, n, by one.
This is the formula that small, and even some larger, calculators
use because, as you are entering data values the calculator
takes the value that you enter, adds it to the running total sumx,
adds the square of the value to the running total sumsqx
and increase the count of the data values, n, by one.
Then, whenever you ask for the standard deviation
the calculator just has to do the last formula above.
The system has the extra advantage that if you realize that somewhere in the data entry
process you made a mistake in entering a data value then it is easy to delete that value.
You hit some button to tell the calculator to remove a value and all it has to do
is ask for the value, subtract it from sumx,
subtract its square from sumsqx, and decrease the number of data items, n, by one.
Of course, once you have the calculator, or once you have some computer software
to do the calculation for you, there is little advantage to knowing these
alternative formuli for finding the standard deviation.
Return to Measures of Dispersion
©Roger M. Palay
Saline, MI 48176 October, 2015
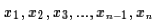 is given by
is given by
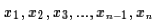 is given by
is given by
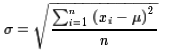
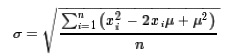
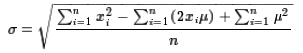
 ,
so we could rewrite the formula as
,
so we could rewrite the formula as
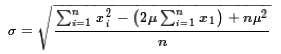 ,
,
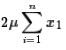 as
as
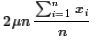 , but that has the factor
, but that has the factor
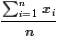 which is our definition of μ.
Therefore,
we can replace
which is our definition of μ.
Therefore,
we can replace 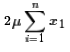 with
with
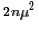 and our formula becomes
and our formula becomes
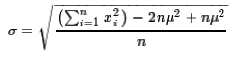

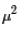 with
with 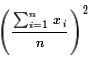 we get
we get