Scientific Notation
Return to Module 0 page
Sometimes we run into very large or very small numbers. For example,
602,214,076,000,000,000,000,000 is Avagadro's number, an important number in science,
is the approximate number of molecules (or atoms if
the substance is an element) in a "mole" of the substance. Or, we could look at
0.000 000 000 000 000 000 000 001 672 621 92 grams
which is the approximate mass of a single proton.
Or, the odds of winning the Powerball jackpot (as constitued on Nov. 24, 2022) on a single bet
are 1 out of 292,201,338 which, expressed as a decimal, is approximately
0.000 000 003 422 298.
Dealng with large and/or tiny numbers is messy at best. We want to find a way to write those numbers where we do not need
to write out all of those trailing or leading zeros. We do this by expressing the value in scientific notation.
Avagrado's number becomes 6.022214076 x 1023
The mass of a proton becomes 1.67262192 x 10-24 grams.
The probabiity of winning the Powerball jackpot becomes
3.422298 x 10-9
In each case, the scientific notation form of a number is a non-zero digit, a decimal point, the rest of the significant digits and
then that number times 10 raised to the appropiate exponent.
To convert a number to scientific notation
- read the number from left to right,
- find the first non-zero digit, write it down;
- follow it by a decimal point;
- follow that by the rest of the digits, stopping when all
remaining digits are 0 or when you run out of digits;
- follow that by "x 10" to indicate "times 10"; and
- then put in the exponent needed to move the decimal point back to its original position.
For example, to write 4,530,000 in scientific notation we would write
4.53 x 10 6
because starting with 4.53 we would have to move the decimal point 6 places to the right, adding the needed 0's, in order to put it
at the end of 4,530,000. Or, to write 0.00000453 in scientific notations we would write
4.53 x 10 -6
because starting with 4.53 we would have to move the decimal point 6 places to the left,
adding the needed 0's in order to put it
in the right place for 0.00000453.
Here are some more examples:
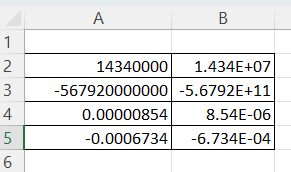
14,340,000 is the same as 1.434 x 107
-567,920,000,000 is the same as -5.6792 x 1011
0.00000854 is the same as 8.54 x 10-6
-0.0006734 is the same as -6.734 x 10-4
Now, having done all of that, let us make a small, notational, switch. Back in the early
days of computers we had no way to print exponents. That is, we had no way to write
10-4. So, instead, we would write 10E-04
and everyone using the computer woud be taught to read
-6.734E-04 as -6.734 x 10-4.
Let us rewrite our examples using this "old computer" form for scientific notation.
14,340,000 is the same as 1.434E+07
-567,920,000,000 is the same as -5.6792E+11
0.00000854 is the same as 8.54E-06
-0.0006734 is the same as -6.734E-04
As it turns out, the spreadsheet program Excel uses exactly this format for expressing scientific
notation. Figure 1 is an image of an Excel spreadsheet showing our example values.
Figure 1
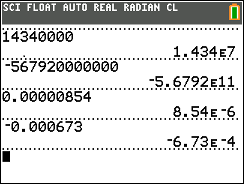
Over time, computer and calculator displays have improved. The TI-83/84 calculators have modified that
"old computer" format to use a slightly smaller E, to not require two digits for
the exponent, and to not use the + sign for positive exponents. We could rewrite our examples in TI-83/84 form as:
14,340,000 is the same as 1.434E7
-567,920,000,000 is the same as -5.6792E11
0.00000854 is the same as 8.54E-6
-0.0006734 is the same as -6.734E-4
Figure 2 is an image of the screen display of those values on a TI-84 calculator.
Figure 2
The design of the TI-83/84 display is really quite old by computer standards. Some computer software,
especially more modern software, has evolved to replace that E by e. That is the
case for the statistical software R.
Figure 3 is an image of the screen display of those values from the console display of an R session.
Figure 3

You might note that R figured out that it would take 4 places to the right of the decimal
to display -567,920,000,000 in scientific notation and, therefore,
R used 4 digits to the right of the decimal on all of the values being displayed by that one command.
To convert a number from scientific notation to expanded, i.e., normal, form
We just reverse the process from above.
- If the scientific notation has a positive exponent then just move the decimal point
that many places to the right, adding 0's as place holders where
needed. Thus, 3.054E+06 becomes 3054000.
- If the scientific notation has a negative exponent then just move the decimal point
that many places to the left. This will require placing 0's in front
of the number in order to hold those places.
Thus, 8.402E-07 becomes 0.0000008402. (You might note that the
number of 0's added between the decimal point and the leading digit of
the original scientific form number is just one less than the magnitude of the exponent. In the example,
the exponent was 7 so we have added 6 place holder 0's between the decimal point and the
8.
Here are a few more examples that use various forms of scientific notation.
4.67805e+11 becomes 467,805,000,000
2.04E-5 becomes 0.0000204
-5.7E04 becomes -57,000.
-9.567e-12 becomes -0.000000000009567
Return to Module 0 page
©Roger M. Palay
Saline, MI 48176 December, 2022



