Linear Regression and the Correlation Coefficient

Return to Topics page
We will start this presentation by considering the values in Table 1.
We can use the work we have done on descriptive statistics to get a "feel" for these values. Figure 1 shows the generation of the same values in R, along with a display of the values (we see that the x values are in L1, and the y values are in L2) and then the summary statistics for the two collections of values.

Figure 1

These are good summaries but they are done on the individual collections. The thought that we might have is that there is some relationship between the x values and the corresponding y values. To get a picture of this we turn to our scatter plot. Figure 2 shows the R commands that can be used to produce the desired plot.

Figure 2

To make it easy for you to copy and paste them into an R session so that you can follow along, the same commands appear here:

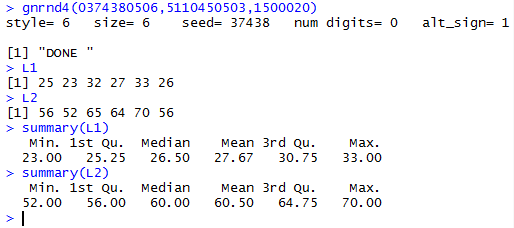
gnrnd4(0374380506,5110450503,1500020)
L1
L2
summary(L1)
summary(L2)
plot( L1, L2, main="Values from Table 1",
      xlim=c(20,35), ylim=c(50,76),
      xaxp=c(20,35,15), yaxp=c(50,76,13),
      xlab="X values", ylab="Y values",
      pch=19, col="blue", las=1 )
abline(h=seq(50,76,2), lty=3, col="darkgray")
abline(v=seq(20,35,1), lty=3, col="darkgray")

The resulting graph is shown in Figure 3.

Figure 3

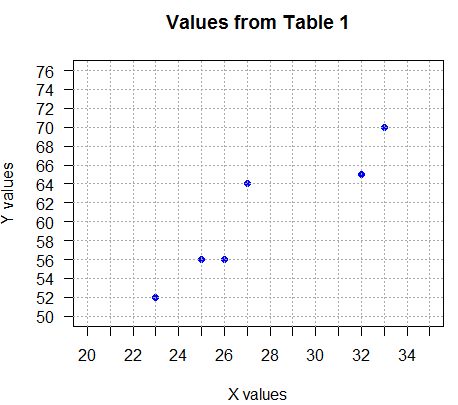
Just looking at Figure 3 one gets the impression that there is a relationship between the x and y values. The larger the x value, the larger, in general, is the y value.

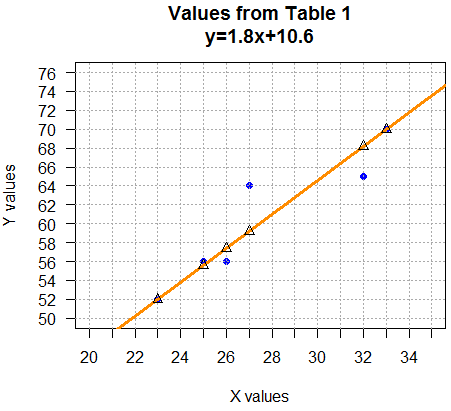
Clearly we cannot draw a single straight line that hits all of the plotted points. However, we could draw one that approximates the trend suggested by those points. Consider the line shown in Figure 4.

Figure 4

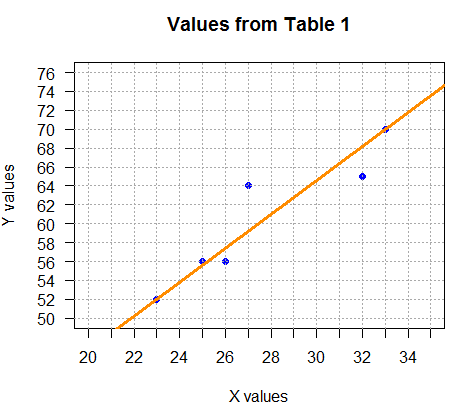
That line represents the relation y=1.8x+10.6 and it was generated by the code abline(a=10.6,b=1.8, col="darkorange", lwd=3). Before we discuss the origin of that line, notice how nicely the line "characterizes", gives us a "feel" for, the relationship between x value and y values. In this way, generating the line is almost a new descriptive statistic.

The line used in Figure 4 came from finding the equation of a line through the two points (23,52) and (33,70). The choice of points was mine. There was no particular logic to it.

Figure 5 shows a different line, given in "green", that someone else might have suggested for characterizing the relationshiop between L1 and L2 values. But is that orange line a better "characterization" than is the green line shown in Figure 5?

Figure 5

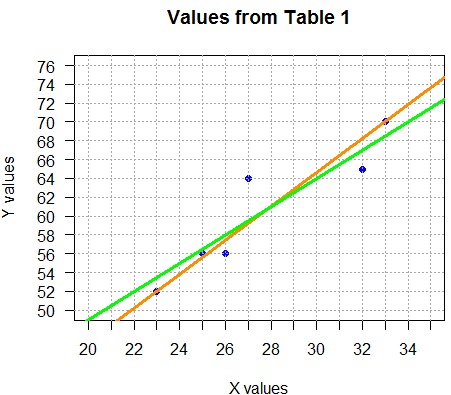
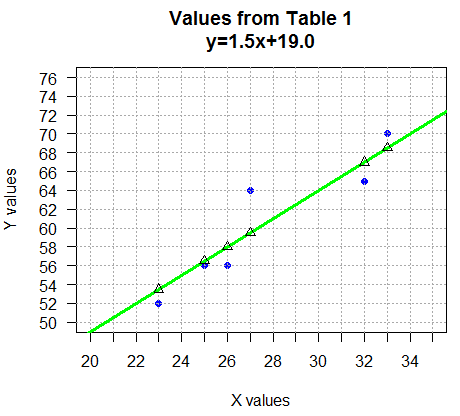
The green line, generated by the code abline(a=19.0,b=1.5, col="green", lwd=3), was defined by finding the equation of the line through the points (22,52) and (34,70), namely, y=1.5x+19.0.

We need some way to evaluate which of the two equations is a better "characterization" of the original data points. That characterization will be to find, for each of the two lines, the sum of the squared differences between the observed values and the expected values. Whichever line has a smaller sum of the squared differences will be the better fitting line.

The observed values are the y values in the original table. The expected values are the y values predicted by our model,which in our case is the equation for the line we are evaluuating.

First,we will evaluate the orange line, that is, find the sum of the squared differences between the observed values and the expected values for the orange line in Figure 5. The equation for that line was y=1.8x+10.6. Figure 6 redisplays the original points (the observed values), the orange line, and it adds the points on that line associated with the x values from the original (x,y) pairs.

Figure 6

Table 2 shows all of the calculations to find the sum of the squared differences between the observed values and the expected values for the orange line in Figure 6.

We can do the same computations for our other line, y=1.5x+19.0. First, we look at the original points, the line we are considering, and the points on that line associated with the x values of the original points.

Figure 7

Then we construct Table 3 holding those computations.

In Table 2 the sum of the squared differences was 35.4. In Table 3 the sum of the squared differences was 33.0. Table 3 has the lower sum of the squared differences and therefore, we say that y=1.5x+19.0 is the better "characterization" of, is a better "fit" for, the relation between the x values and the y values back in Table 1.

Although it is nice to know that y=1.5x+19.0 is a better fit, that leaves us with the question of "Is there another equation that is an even better fit?" Or rather, is there a way to find the equation with the best fit to the original data points? That answer is yes, but the computation of the coefficient of x and the intercept is a bit tedious. Rather than present that computation here we have a different web page, Computing the Linear Regression, that walks through the computation. For us, at this point, we just want to see how to find those values using R.

The command in R to compute the linear regression values (the intercept and the coefficient) is the lm() function. This is the linear model function, thus the name lm. We use the full command lm(L2~L1) to call this function. There are a few things to note here.

The order of the variables is important, and perhaps, not what was expected.
The general model is y=mx+b, but the command has the known values for y, the L2 in our case, in the first position, and the known values for x, the L1 in our case, in the second position.
The ~ character, named "tilde", is usually in the upper left corner of the keyboard.
The command is much more powerful than we will experience in this course.
The default output of the command is minimal, giving us the values we want, but not much more.
We can get much more information from the command with just a little effort.

Figure 8 shows the use of the lm(L2~L1) command and the default output of that command.

Figure 8

The output shown in Figure 8 tells us that the equation y=1.601x+16.210 is the equation that is the best fit for our original data. [One thing to note here is that these are rounded values and that if we had more digits in the displayed values we might have a slightly better fitting equation. However, the difference in the "fit" will hardly be noticable.] We can construct a new table, Table 4, to examine the computations for the sum of the squared differences based on this new equation.
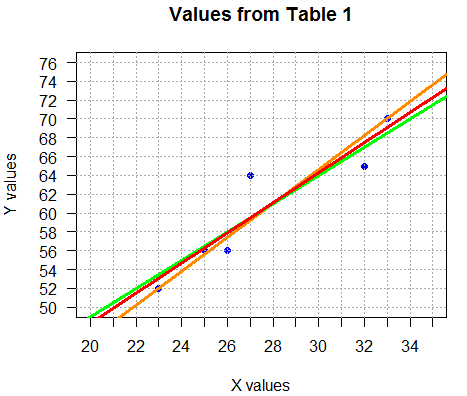
Notice that the sum of the squared differences, 32.19339, is lower than the values we found by just guessing at the line of best fit. Furthermore, we can graph the equation on our graph, shown as the red line in Figure 9, by using the command abline(a=16.210,b=1.601, col="red", lwd=3).

Figure 9

Before we go on, we should take a moment to talk about the different ways to state, in general terms, the equation of a line. In math classes, starting with pre-algebra and extending right through Calculus, we consistently say that the "slope-intercept form" of a straight line is given as y = mx + b, where m is the slope of the line and b is the y-coordinate of the y-intercept, meaning that the line intersects the y-axis at the point (0,b). Sometimes in statistics this same form is written as y = ax + b, where a is the slope and b is the y-coordinate of the y-intercept.

Other times in statistics, the slope-intercept form is written as y = a + bx, where a is the y-coordinate of the y-intercept and b is the slope. This particular convention is the one used by R, extensively. It is this convention that dictated our assignment of values in abline(a=10.6,b=1.8, col="darkorange", lwd=3) so that a=10.6 makes the y-intercept be 10.6 and b=1.8 makes the slope, that is the coefficient of x, be 1.8, yielding the equation y=10.6+1.8x. Similarly, the code abline(a=16.210,b=1.601, col="red", lwd=3) yields y=16.21+1.601x.

This style continues to be evident in the arrangement of values shown back in Figure 8. The intercept value is given first, and then we find the coefficient of x value.

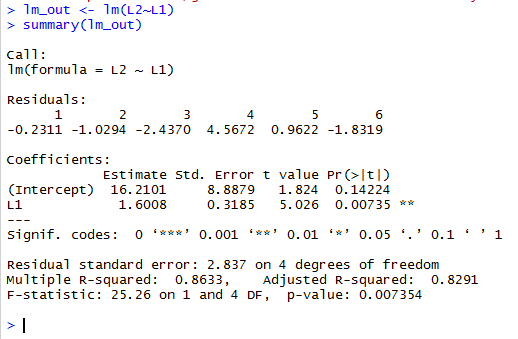
As noted above, the lm() command actually produces much more than the few values displayed by default. We can see this by assigning the result of the lm() command to a variable, and then asking for a summary of that variables, as shown in Figure 10.

Figure 10

The command lm_out <- lm(L2~L1) does not produce any output, but the following summary(lm_out) generates many lines of information.

Reading from the top of the display the initial few lines are identical to those that are part of the default display, namely a recap of the model being used, L2~L1. Under that we find a section titled Residuals:. The residuals are the observed minus the expected values. We actually saw these same values in the fourth column of Table 4.

Below the residuals is a section titled Coefficients:. In here we find our by now familiar intercept, 16.2101 and coefficient of x, that is, of the variable we associate with L1, namely, 1.6008. You might notice that these values have an extra significant digit compared to the values we first saw back in Figure 8. There was an assertion above, just after Figure 8, that increasing the number of significant digits would not significantly change the the sum of the squared differences which was 32.19339 back in Table 4. We can check out that assertion by looking at Table 5. .

A slight improvement, though if we drew the two lines the difference would most likely be less than the thickness of the lines.

Although there is much more information in Figure 10, the only part of it that we want to notice at this time is the piece given as Multiple R-squared: 0.8633. Technically, this is the square of the correlation coefficient, a value that is discussed just below. The R-squared value tells us the percent of variation shown in the original data that is explained by the linear regression model that the lm() function computed.

The lm() function computes the line of best fit for the original data values. It would be nice to know just how good that fit is? The correlation coefficient helps us to determine that. This is another complex computation, but one that is done for us by a simple R command, namely, the cor() function. 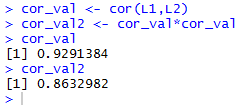Applying that function to our current data via the cor(L1,L2) function call and assigning the result to the variable cor_val allows us to also compute, via the statement cor_val2<-cor_val*cor_val, the square of the correlation coefficient. This is shown in Figure 11, along with a display of the values stored in the two variables.

Figure 11

The first thing we can do here is to confirm that the value stored in cor_val2, which we just formed as the square of the correlation coefficient, is indeed, the same value that we saw in Figure 10 where it was called Multiple R-squared:. And, indeed, these are the same value.

The correlation coefficient is commonly called r. The possible values for r range from +1.0 to -1.0. The closer the computed r value is to either extreme the better the "fit" of the linear model, the line, to the actual data. The closer the computed value of r is to 0 the worse is the "fit" of the line to the data. Values close to -1.0 reflect a line that has a negative slope. The best way to see all of this is with some examples.

For each of the following examples we will

Generate the data
Display the x and y values (in L1 and L2, usually)
Use lm() to generate the linear model
Store that linear model in a variable
Display the linear model to see the Intercept and coefficient
Use cor() to compute and display the correlation coefficient
Plot the points and the regression line

[Note that the actual code used to generate the following figures, not only is shown in those Figures but also is provided as straight text at the end of this web page.

For the first example, we want to process the values in Table 6.
Generate and display the data. Find the linear regression and the correlation coefficient.

Figure 12

The resulting equation is y=17.305 + 1.794x, an equation with a positive slope. The correlation coefficiient is 0.9935502, a value close to 1.0 so we expect the points to be close to the line. Note that the square of the correlation coefficient is about .987 so the model explains about 98.7% of the variation in the data.

Give the commands to produce the plot.

Figure 13

The resulting graph.

Figure 14

Indeed, the points are quite close to the line, and the line has an increasing slope. Thus, as the x values increase so do the y values.

For the second example, we want to process the values in Table 7.
Generate and display the data. Find the linear regression and the correlation coefficient.

Figure 15

The resulting equation is y=24.149 + 1.476x. The correlation coefficient is 0.7133098, a value well below 1.0 so we expect the points to be spread away from the line. Note that the square of the correlation coefficient is close to .5 which means that the model explains only about half of the variation in the data.

Give the commands to produce the plot.

Figure 16

The resulting graph.

Figure 17

The resulting equation is y=47.924 - 1.722x. The correlation coefficiient is -0.9854415, a value close to -1.0 so we expect the points to be close to the line. Note that the square of the correlation coefficient is close to .97 which means that the model explains about 97% of the variation in the data. The graph will have a negative slope suggesting that as x values go up the corresponding y values will go down.

Give the commands to produce the plot.

Figure 19

The resulting graph.

Figure 20

As expected, the points are close to the line. This is indicates a close relationship between the x values and their corresponding y values.

The regression line does have a negative slope and there is at least a "feeling" that larger x values are associated with smaller y values. This is consistent with the significant (very close to 1 or -1) and negative correlation coefficient.

For the fourth example, we want to process the values in Table 9.
Generate and display the data. Find the linear regression and the correlation coefficient.

Figure 21

The resulting equation is y=49.832 - 2.091x. The correlation coefficiient is -0.6717215, a value well above -1.0 so we expect the points to be spread away from the line. Note that the square of the correlation coefficient is close to .45 which means that the model explains less than half of the variation in the data.

Give the commands to produce the plot.

Figure 22

The resulting graph.

Figure 23

As expected, the points are scattered about the line. That is, the line gives us an overall feel for a slight relationship between the x values and their corresponding y values. However, the scattering of the points means that this relationship, if it exists at all, is a weak one and that there are other things influencing the y values.

The regression line does have a positive slope and there is at least a "feeling" that larger x values are associated with larger y values. This is consistent with the low but positive correlation coefficient.

For the fifth example, we want to process the values in Table 10.
Generate the data. Note in Figure 24 that the x values and the y values are generated independently via two separate instances of the gnrnd4() function. The two resulting collections of values are stored in new variables, x_vals and y_vals, and then those varaibles are used in the rest of the commands that we use to display the data, find the linear regression and the correlation coefficient.

Figure 24

The resulting equation is y=36.1405 - 0.6436x. The correlation coefficiient is -0.2971946, a value well above -1.0 so we expect the points to be spread away from the line. Note that the square of the correlation coefficient is close to .088 which means that the model explains less than 9% of the variation in the data. Although the lm() function has produced a linear model that is the "line of best fit", the fact that it explains less than 9% of the variation in the data tells us that there really isn't a linear relation between the x values and the y values.

Give the commands to produce the plot.

Figure 25

The resulting graph.

Figure 26

Again, the points are scattered. Given that the coordinates of the points were generated independently this is just what we should expect. As it turned out, by chance, there we no low y values that were associated with the lowest of the x values. That happenstance gave the regression equation a slight negative slope. Fortunately, the rest of the data is scattered enough that the overall correlation coefficient indicated that even the est fitting linear model is not a good characterization of a reation between the two variables.

The following lines give the code used to generate all of the work from Figure 12 to through Figure 26. The code is provided here so that you could, if so desired, copy it, possibly in pieces, and paste it into an R session so that you can see all of this working.
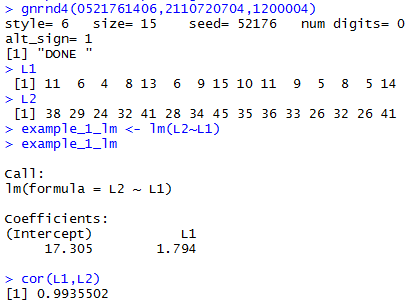
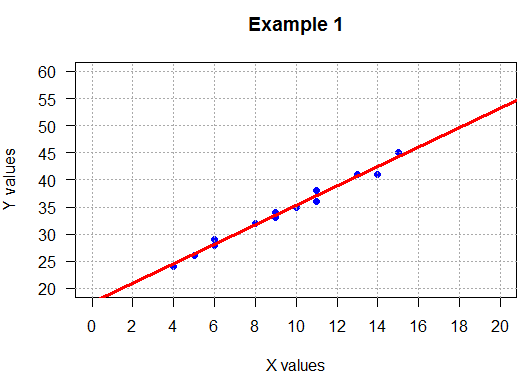
## positive slope, tight gnrnd4(0521761406,2110720704,1200004) L1 L2 example_1_lm <- lm(L2~L1) example_1_lm cor(L1,L2) plot( L1, L2, main="Example 1", xlim=c(0,20), ylim=c(20,60), xaxp=c(0,20,10), yaxp=c(20,60,8), xlab="X values", ylab="Y values", pch=19, col="blue", las=1 ) abline(h=seq(20,60,5), lty=3, col="darkgray") abline(v=seq(0,20,2), lty=3, col="darkgray") abline(example_1_lm, col="red", lwd=3) ############## ## positive slope, loose 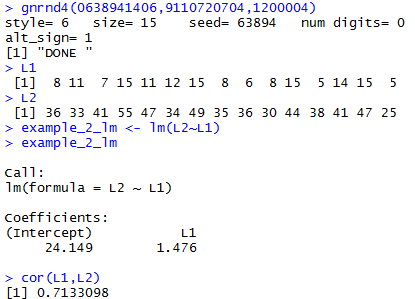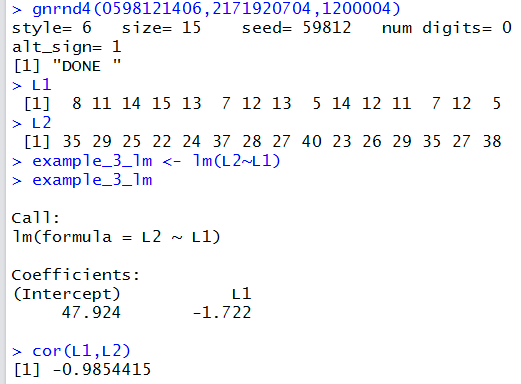gnrnd4(0638941406,9110720704,1200004) L1 L2 example_2_lm <- lm(L2~L1) example_2_lm cor(L1,L2) 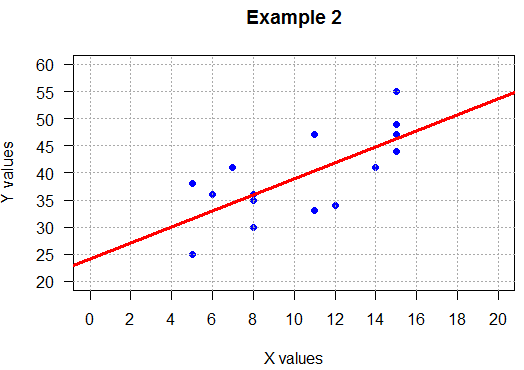plot( L1, L2, main="Example 2", xlim=c(0,20), ylim=c(20,60), xaxp=c(0,20,10), yaxp=c(20,60,8), xlab="X values", ylab="Y values", pch=19, col="blue", las=1 ) abline(h=seq(20,60,5), lty=3, col="darkgray") abline(v=seq(0,20,2), lty=3, col="darkgray") abline(example_2_lm, col="red", lwd=3) ############## ## negative slope, tight 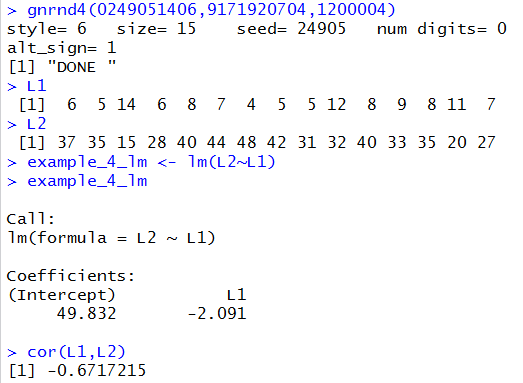gnrnd4(0598121406,2171920704,1200004) L1 L2 example_3_lm <- lm(L2~L1) example_3_lm cor(L1,L2) 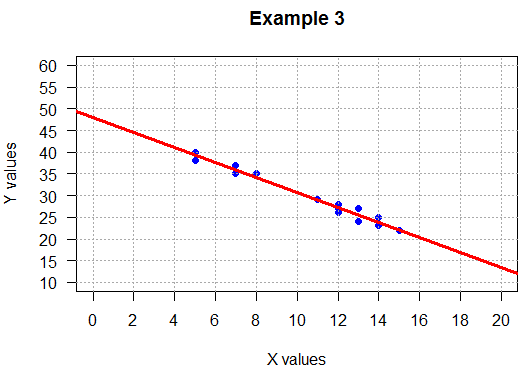plot( L1, L2, main="Example 3", xlim=c(0,20), ylim=c(10,60), xaxp=c(0,20,10), yaxp=c(10,60,10), xlab="X values", ylab="Y values", pch=19, col="blue", las=1 ) abline(h=seq(10,60,5), lty=3, col="darkgray") abline(v=seq(0,20,2), lty=3, col="darkgray") abline(example_3_lm, col="red", lwd=3) ############## ## 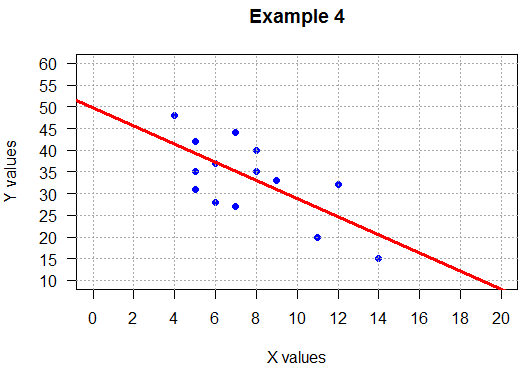negative slope, loose gnrnd4(0249051406,9171920704,1200004) L1 L2 example_4_lm <- lm(L2~L1) example_4_lm cor(L1,L2) plot( L1, L2, main="Example 4", xlim=c(0,20), ylim=c(10,60), xaxp=c(0,20,10), yaxp=c(10,60,10), xlab="X values", ylab="Y values", pch=19, col="blue", las=1 ) abline(h=seq(10,60,5), lty=3, col="darkgray") abline(v=seq(0,20,2), lty=3, col="darkgray") abline(example_4_lm, col="red", lwd=3) ############## ## 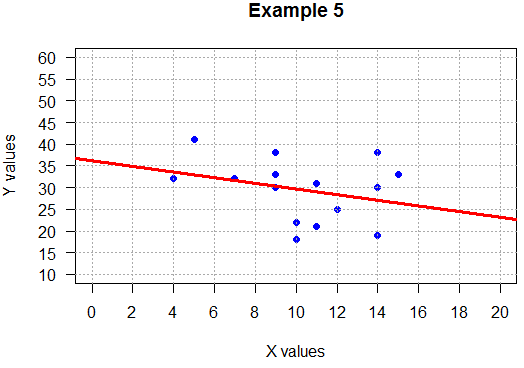no relation 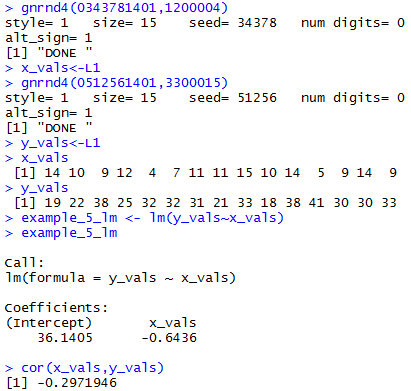gnrnd4(0343781401,1200004) x_vals<-L1 gnrnd4(0512561401,3300015) y_vals<-L1 x_vals y_vals example_5_lm <- lm(y_vals~x_vals) example_5_lm cor(x_vals,y_vals) plot( x_vals, y_vals, main="Example 5", xlim=c(0,20), ylim=c(10,60), xaxp=c(0,20,10), yaxp=c(10,60,10), xlab="X values", ylab="Y values", pch=19, col="blue", las=1 ) abline(h=seq(10,60,5), lty=3, col="darkgray") abline(v=seq(0,20,2), lty=3, col="darkgray") abline(example_5_lm, col="red", lwd=3)

Return to Topics page
©Roger M. Palay Saline, MI 48176 November, 2015