Converting Fraction Forms

Return to Module 0 page
We have three ways that we use to represent fractions values: common fractions, decimal fractions, and percentages. It is important to be able to convert a value from one form to another. Some of the more common values, those that should just be recognized rather than calcuated, are give in Table 1 below. \

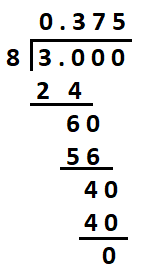
Table 1
What should be easily recognizeable conversions

common
fraction

1 / 2

1 / 4

3 / 4

1 / 5

2 / 5

3 / 5

4 / 5

1 / 8

3 / 8

5 / 8

7 / 8

1 / 10

3 / 10

7 / 10

9 / 10

decimal
fractions

0.5

0.25

0.75

0.2

0.4

0.6

0.8

0.125

0.375

0.625

0.875

0.1

0.3

0.7

0.9

percents

50%

25%

75%

20%

40%

60%

80%

12.5%

37.5%

62.5%

87.5%

10%

30%

70%

90%

All of us should be able to convert any of these values from one form to another. But there are fractions not shown in the table. What about all of those? Consideration of those "other" fractions really falls into 5 categories. These are demonstrated by

Why isn't
4 / 10
in the table?
Why isn't 0.14 in the table, and how do we deal with that?
Why isn't
1 / 3
in the table, and how do we deal with that?
Why isn't 7
3 / 25
in the table, and how do we deal with that?
Why isn't
3.45 / 13.8
in the table, and how do we deal with that?

However, before we attack those five issues, let us return to the table. We should just know these values and conversions between forms, but how does one go about computing alternative forms for the values in Table 1? For this we will look at the following conversions common fraction ⇔ decimal fraction ⇔ percentage and we do so in a pairwise manner.

Consider common fraction ⇔ decimal fraction.

First, look at converting from common fraction form to decimal form. If we start with

3 / 8

how do we "compute" the decimal equivalent, 0.375? We do this by dividing the numerator, the number on top in the fraction, by the denominator, the number on the bottom of the fraction. In this case, that is 3 divided by 8. By hand this looks like

Figure 1

Doing the division on a TI-84 calculator gives us

Figure 2

Some examples of converting common fractions to decimals are:

3 / 16

becomes 0.1875

9 / 40

becomes 0.225

73 / 200

becomes 0.365

235 / 32

becomes 7.34375

Figure 3

Then consider converting from decimal form to the common fraction form. Starting with 0.625, how do we compute the common fraction equivalent

5 / 8

? We do this by writing the decimal number, without the decimal point, as the numerator of our fraction and then writing the denominator as a 1 followed by the same number of 0's as we have digits in our decimal fraction. In this case, because there are 3 digits to the right of the decimal point in 0.625 we start with

625 / 1000

Then we reduce that fraction. Reducing a fraction is an important process to know, however, it is not one of the topics currently covered in Module 0 material. For now we will just note that to reduce a fraction we will try to find a number, greater than 1, that evenly divides both the numerator and the denominator. If we can find such a number, then we use it to divide both the numerator and the denominator. We keep doing this process until we cannot find any such number greater than 1. At that point the fraction is reduced. In our current case,

625 / 1000

, both numerator and denominator can be evenly divided by 5. We do that and find

625 / 1000

125*5 / 200*5

125 / 200

but 125 and 200 are both evenly divisible by 5. We do that and find

625 / 1000

125 / 200

25*5 / 40*5

25 / 40

, but 25 and 40 are both evenly divisible by 5. We do that and find

625 / 1000

125 / 200

25 / 40

5*5 / 8*5

5 / 8

. There are no other values that evenly divide both 5 and 8 so

5 / 8

is our reduced common fraction form.

For many decimal values, the TI-84 makes this very easy. Just enter the decimal value and then press the

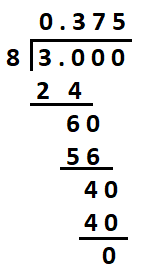
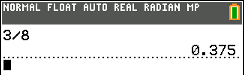
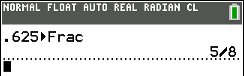
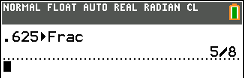
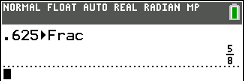
button and select option 1,

, and then press the

. The calculator produces the fraction.

5 / 8

. On older TI-84's or on a newer one using the CLASSIC mode, the screen looks like:

Figure 4

On a newer TI-84 using the MATHPRINT mode, that same command appears as

Figure 5

Here are 2 more examples.

Convert 0.3816 to a fraction.
0.3816 =

3816 / 10000

954 * 4 / 2500 * 4

954 / 2500

477 * 2 / 1250 * 2

477 / 1250

Convert 0.4375 to a fraction.
0.4375 =

4375 / 10000

875 * 5 / 2000 * 5

875 / 2000

175 * 5 / 400 * 5

175 / 200

35 * 5 / 80 * 5

35 / 80

7 * 5 / 16 * 5

7 / 16

The most discerning readers will have noticed that all of the fractions shown above, at least in their reduced versions, have denominators that have only 2 and/or 5 as factors. This is not an accident. Fractions, in reduced form that have values other than 2 or 5 as factors of the denominator will be repeating decimal fractions. For example,

1 / 3

= 0.3333 or

8 / 13

= 0.615384615384 or

3352 / 4625

= 0.724756756756 or

93 / 2860

= 0.03251748251748.
Converting repeating decimals to fractions takes a little algebra. This is more than we want to cover here. Our discussion here is limited to what are often called terminating decimals. That is, we will look at 0.1414 but not at 0.141414. We would need a different web page to demonstrate converting repeating decimals to fractions.

Now look at the decimal fraction ⇔ percentage conversions.

The "percent sign", the % character, is just an abbreviation for

1 / 100

with an implied multiplication between the original number and the

1 / 100

. Thus, the percent 67% really means 67*
1 / 100
But dividing a value by 100 results in moving the decimal point two places to the left. Therefore, 67% can be written as 0.67. Our general rule for converting a percentage to a decimal format is to just move the decimal point two places to the left. For example
38% = 0.38, or
4% = 0.04, or
273% = 2.73, or
44.62% = 0.4462.

To go the other way, from a decimal fraction to a percentage we just move the decimal point 2 places to the right and add the percent sign. Thus,
0.59 = 59%, or
0.09 = 9%, or
1.42 = 142%, or
0.27935 = 27.935%.

To finish this topic, we will return to the five questions posed above. This time we will provide an answer to each question.

Why isn't
4 / 10
in the table? It is not in the table because we can reduce it.
4 / 10
=
2 / 5
and that is in the table.
Why isn't 0.14 in the table, and how do we deal with that? We actually did see that we can convert 0.14 to a percentage, 14%, or to fraction 0.14 =
14 / 100
=
7 / 50
.
Why isn't
1 / 3
in the table, and how do we deal with that? 1 / 3
is a repeating decimal. If we tried to divide the numerator, 1, by the denominator, 3, we would get 0.333333333. We had a note above that said that we would need a little algebra to work out the conversion mathematically and that we would save that for a different web page. One way to deal with this here is just to note and remember that 1 / 3
= 0.333333333 = 33
1 / 3
% and
2 / 3
= 0.6666666 = 66
2 / 3
% and not worry about it beyond that.
Why isn't 7
3 / 25
in the table, and how do we deal with that? We recall that 7
3 / 25
= 7 +
3 / 25
. We convert 3 / 25
to its decimal equivalent, 0.12 and then add that to the 7 to get 7.12 which is equivalent to 712%.
Why isn't
3.45 / 13.8
in the table, and how do we deal with that? This is the first time that we have decimal values in the numerator or the denominator of a fraction. One way to deal with this is just to move the decimal points far enough to the right so that we no longer have that situation. In this example we would need to move the decimal points two places to the right. Thus,
3.45 / 13.8
=
345 / 1380
then reduce that fraction
345 / 1380
=
69*5 / 276*5
=
69 / 276
=
23*3 / 92*3
=
23 / 92
=
1*23 / 4*23
=
1 / 4