 Figure 1
Figure 1
Return to the Main Math 293 Chapter 14 Topics page
Revised July 23, 2013
Some images on this page have been generated via AsciiMathML.js.
For more information see:
www.chapman.edu/~jipsen/asciimath.html.
The problem statement is:
Find the area of the region between `theta=0.5` and `theta=1.4`,
and between `r=6+sin(12theta)` and `r=9+sin(18theta)`.
Express your answer rounded to the nearest thousandths.
[Two small reminders: `intsin^2(ax)dx\quad=\quad x/2-(sin(ax)cos(ax))/(2a)+C`
and `intcos^2(ax)dx\quad=quadx/2+(sin(ax)cos(ax))/(2a)+C`]
The written solution to this is given in the
pencast of this problem.
That written solution ends with the task of evaluating
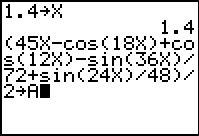
`1/2(45theta - cos(18theta) + cos(12theta) - (sin(36theta)/(72) + sin(24theta)/48 |_0.5^1.4 )`
To do this on the calculator we can assign 1.4 to x and then enter
the entire expression, using `X` in place of `theta`.
I did this, along with dividing the expression by 2 and storing the result in A.
Here is an image of the calculator screen at that point.
 Figure 1
Figure 1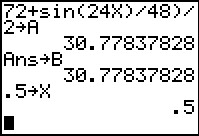 Figure 2
Figure 2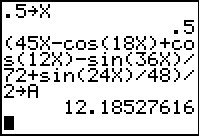 Figure 3
Figure 3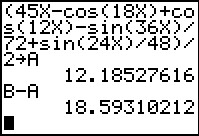 Figure 4
Figure 4As noted on the pencast, we did not need to do all of the work that we did. In fact we had no particular need to simplify some of the exressions. Furthermore, the TI-83/84 calulators will actually do the integration for us. Not the symbolic integration, but the it will compute the definite integral if we can get the problem in that form. In the pencast we made note of the point in the solution where we said that we needed to find `int_0.5^1.4 ((9+sin(18theta))^2)/2 - ((6+sin(12theta))^2)/2 d theta`. We can have the calculator do this for us. The first step is to find the right command. That command is fnInt( and it is on the MATH options page:
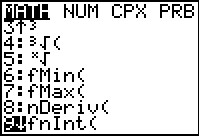 Figure 5
Figure 5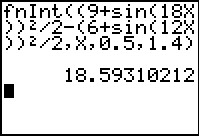 Figure 6
Figure 6©Roger M. Palay
Saline, MI 48176
July, 2013