Chapter 15
Section 15.1: Vector Fields

• Definition of Vector Field
  1. A vector field over a plane region R is a function F that assigns a vector F(x,y) to each point in R.
  2. A vector field over a solid region Q in space is a function F that assigns a vector F(x,y,z) to each point in Q.
• The gradient is an example of a vector field. After all, for each point in the domain the gradient is just a vector valued function defined at each such point.
• Note the subtle deviation from the general definition of a vector as we start to tie the vector to the point that generated it. Thus, the diagrams in the book have the vectors as a single instance (remember that a vector has direction and magnitude, but not a unique position) with its tail at the point that generated the direction and magnitude of the vector.
• What becomes important here is the nomenclature since these symbols are used extensively in physics and engineering to describe certain phenomina.
• Graphing vector fields
  One web site
  Second site
  Third (3d) site, but I have not figured it out
• Velocity fields -- common example of fluid motion in a pipe.
• Gravitations force between a particle of mass `m_1` located at `(x,y,z)` by a particle of mass `m_2` located at the origin, `(0,0,0)`, is given by `F(x,y,z) = (-Gm_1m_2)/(x^2+y^2+z^2)bbu`, where `bbu` is the unit vector pointing from one object to the other. In the following diagram the objects are not placed in a coordinate syste. The diagram merely shows that the force acts both ways.
  

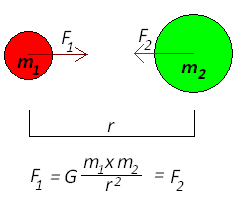
  Returning to having the two points located in a coordinate system, the point `(x,y,z)` exists at the end of the vector, in standard position, `bbr=xbbi+ybbj+zbbk`. Thus the value `(x^2+y^2+z^2)` can be expressed as `||bbr||^2` and `bbu` can be expressed as `bbr/(||bbr||)`, which means that we can rewrite the equation as `F(x,y,z)=(-Gm_1m_2)/(||bbr||^2)((bbr)/(||bbr||))`.

• Kepler's Laws: http://groups.physics.northwestern.edu/vpl/mechanics/planets.html not working with current Java
• Kepler's Laws: http://demonstrations.wolfram.com/TheCelestialTwoBodyProblem/ needs preliminary software, free
• Electric force fields: Coulomb's Law: again, one particle at `(0,0,0)` and another at `(x,y,z)`, where `bbr = xbbi + ybbj + zbbk`, with the particles having charges of `q_1` and `q_2`, and a unit vector `bbu = bbr/(||bbr||)`, and `c` is a constant, then
  `F(x,y,z) = (cq_1q_2)/(||bbr||^2) bbu`.
• A vector field `bbF(x,y,z)=M(x,y,z)bbi+N(x,y,z)bbj+P(x,y,z)bbk` is continuous at a point `(x_0,y_0,z_0)` if and only if each of the component functions, M, N, and P, is continuous at `(x_0,y_0,z_0)`.
• Definition of inverse square field
  `bbr(t) = x(t)bbi + y(t)bbj + z(t)bbk`,
  `bbF(x,y,z) = (k)/(||bbr||^2) bbu`, where `k` is a real number and `bbu = (bbr)/(||bbr||)` is a unit vector in the direction of `bbr`
• Definition of a Conservative Vector Field: A vector field `bbF` is called conservative if there exists a differentiable function `f` such that `bbF = grad f`. The function `f` is called the potential function for `bbF`.
• Every inverse square field is conservative.
• Test for conservative vector field in the plane.
  Let `M` and `N` have continuous first partial derivatives on an open disk `R`. The vector field given by `bbf(x,y) = Mbbi +Nbbj` is conservative if and only if `(del N)/(del x) = (del M)/(del y)`
• Definition of Curl of a Vector Field
  The curl of `bbF(x,y,z) = Mbbi +Nbbj + Pbbk`   is
  `curl\quad bbF(x,y,z) = grad xx bbF(x,y,z)`

  `curl \quad bbF(x,y,z) = ( (del P)/(del y) - (del N)/(del z))bbi - ( (del P)/(del x) - (del M)/(del z))bbj + ( (del N)/(del x) - (del M)/(del y))bbk`

  Note that we seem to be looking at the cross product (`xx`) of two vectors when we write `grad xx bbF(x,y,z)`. If we go back to the definition of `grad` and we think of it as the differential operator so: `grad = del/(del x)bbi +del/(del y)bbj + del/(del z)bbk` and given that `bbF(x,y,z)=Mbbi +Nbbj+Pbbk`, then it does look line we have two vectors and we recall that we could write the cross product of two vectors in determinant form as:
  `grad xx bbF(x,y,z) = |[bbi,bbj,bbk],[del/(del x),del/(del y),del/(del z)],[M,N,P]|`, so

  `grad xx bbF(x,y,z) = ( (del P)/(del y) - (del N)/(del z))bbi - ( (del P)/(del x) - (del M)/(del z))bbj + ( (del N)/(del x) - (del M)/(del y))bbk`

  Also note that if we had done a simialar thing for the two variable situation then we might have looked at `|[del/(del x),del/(del y)],[M,N]|` as producing `(del N)/(del x) - (del M)/(del y)` and if that is set to 0 that is the same as saying `(del N)/(del x) = (del M)/(del y)`.

• If ` curl \quadbbF = bb0` then `bbF` is said to be irrotational.
• Test for Conservative vector Field in Space:
  Suppose that `M`, `N`, and `P` have continuous first partial derivatives in an open sphere `Q` in space. The vector field given by `bbF(x,y,z) = Mbbi +Nbbj+Pbbk` is conservative if and only if `curl\quad bbF(x,y,z) = bb0`, and that is equivalent to having `(del P)/(del y) = (del N)/(del z )`, `(del P)/(del x) = (del M)/(del z )`, and `(del N)/(del x) = (del M)/(del y )`.
• Divergence of a Vector Field:
  
  1. The divergence of `bbF(x,y) = Mbbi + Nbbj`  is

     `div   bbF(x,y) = grad • bbF(x,y) = (del M)/(del x) + (del N)/(del y)`

  2. The divergence of `bbF(x,y,z) = Mbbi + Nbbj + Pbbk`  is

     `div   bbF(x,y,z) = grad • bbF(x,y,z) = (del M)/(del x) + (del N)/(del y) + (del P)/(del z)`

  3. If `div   bbF = 0 ` then `bbF` is said to be divergence free.
• Divergence and Curl
  If `F(x,y,z) = Mbbi + Nbbj + Pbbk` is a vector field and `M, N, "and" P` have continuous second partial derivatives, then

  `div(curl bbF) = 0`.