Here is a specific problem:

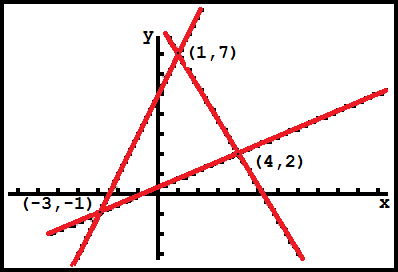
Find a change of variables for the triangular region with corners at `(-3,-1)`, `(1,7)`, and `(4,2)` giving rise to the equations for the sides as `5x+3y=26`, `3x-7y=-2`, and `2x -1y = -5`
To do this let		`u=2x-1y` `v=5x+3y`	(1)
Let us eliminate `y` To do thismultiply the top equation by 3		`3u=6x-3y` `v=5x+3y`	(2)
Add the two equations to eliminate the y's		`3u + v = 11x`	(3)
or		`x =(3u+v)/11`	(4)
Then we want to solve for y We could do this in different ways we could return to (1) and eliminate x we could substitute (4) into one of the equations in (1) We will do the second of these, namely, we will restate `u=2x-1y` substituting the value of (4)		`u = 2( (3u+v)/11 ) - 1y`	(5)
multiply both sides by 11 to clear the fraction		`11u = 6u + 2v -11y` `5u -2v = 11y` `2v - 5u = 11y`	(6)
or		`y =(2v-5u)/11`	(7)
Return to the original equations, and change variables
`5x + 3y = 26` yields		`5((3u+v)/11) + 3((2v-5u)/11) = 26`	(8)
Multiply both sides by 11 to clear fractions and then simplify		`5(3u+v) + 3(2v-5u) = 286` `15u + 5v +6v - 15u = 286` `11v = 286` `v=26`	(9)
`3x - 7y = -2` yields		`3((3u+v)/11) - 7((2v-5u)/11) = -2`	(10)
Multiply both sides by 11 to clear fractions and then simplify		`3(3u+v) - 7(2v-5u) = -22` `9u + 3v - 14v + 35u = -22` `44u - 11v = -22` `4u - 1v = -2`	(11)
`2x - 1y = -5` yields		`2((3u+v)/11) - 1((2v-5u)/11) = -5`	(12)
Multiply both sides by 11 to clear fractions and then simplify		`2(3u+v) - 1(2v-5u) = -55` `6u + 2v - 2v + 5u = -55` `11u = -55` `u=-5`	(13)

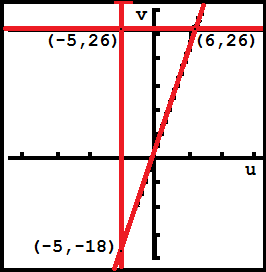
Here are images, originially from a calculator but touched up a bit, of the two systems:
  

Finding areas of triangles is not all that challenging, but it is clear that finding the area of the `uv`-palne triangle is a bit easier than finding the area of the `xy`-plane triangle. In particular, the `uv`-plane triangle has height of 44 and a width of 11, so the area is 44*11/2 or 242 square units.

The tansformations that we found, expressed as
`x=(1/11)(3u+v)` and `y=(1/11)(-5u+2v)`
can be used to find the Jacobian of `x` and `y` with respect to `u` and `v`.

`(del(x,y))/(del(u,v)) = |[(del x)/(del u),(del x)/(del v)],[(del y)/(del u),(del y)/(del v)]| = (del x)/(del u) (del y)/(del v) - (del y)/(del u) (del x)/(del v) `

`(del(x,y))/(del(u,v)) = |[3/11,1/11],[-5/11,2/11]| = 3/11 *2/11 - 1/11 * (-5)/11 = 6/121 +5/121 = 11/121 =1/11`

Then, the change of variables theorem gives us the general statement

`int_rintf(x,y)dxdy = int_Sintf(g(u,v),h(u,v))|(del(x,y))/(del(u,v))| du dv`

And, in this particular case, where we know the Jacobian, to find the area of `R` we have `f(x,y)=1` which means that `f(g(u,v),h(u,v))=1` so we are looking at

`int_Rintdxdy = int_Sint|1/11| du dv =|1/11|int_Sint du dv`

However, as noted above, the area of `S` is 242 square units, so the area of `R` must be `22` square units. Fortunately for us, we have an alternative method of finding the area of `R` so we can check our work. In particular, if we look at the two vectors that form adjacent sides of the triaangle `R` we can compute the area of the triangle by looking at half the magnitude of the cross product of those vectors (we use half because the formula is used for the parallelogram, of which the triangle is just one half). Using the point `(-3,-1,0)` [note that we express this in three dimensions so that we can take a cross-product] as the start of the two vectors, we get the vector to the point `(1,7,0)` as `(:4,8,0:)` and the vector to the point `(4,2,0)` as `(:7,3,0:)`. The cross product of these two vectors is `(:0,0,4*3-8*7:)` which simplifies to `(:0,0,-44:)` and the magnitude of that vector is just `44`, which if we take half of it yields `22`, confirming our earlier work.

Another, non-calculus, method for getting the area of `R` would be to draw the horizontal line through the point `(4,2)` as shown below.

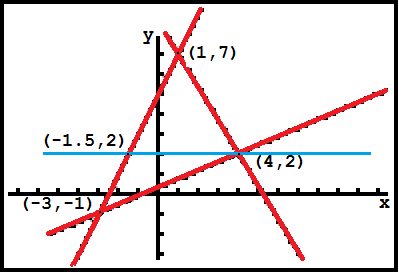
The point where this line hits the left edge of the triangle is the point (-1.5,2). This has divided the original triangle into two new triangles, one having a height of 5 units and the other a height of 3 units, and both have the common base of 5.5 units. Thus, the sum of the areas of the two new triangles is `1/2(5.5)5+1/2(5.5)3 = 1/2(5.5)8 = 22`.