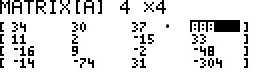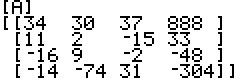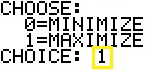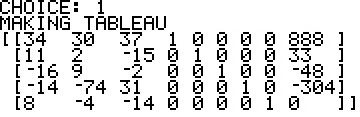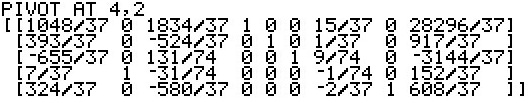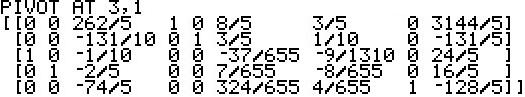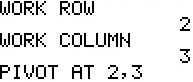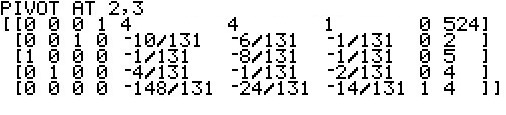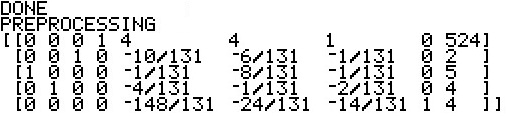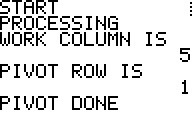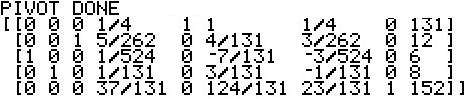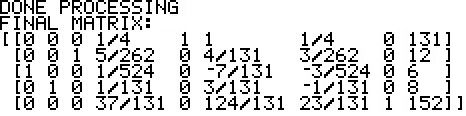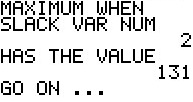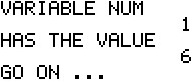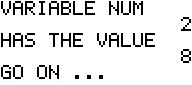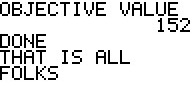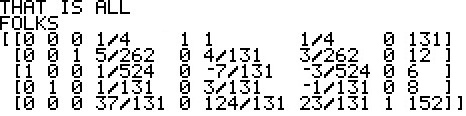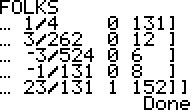Linear Programming Problem -- Simplex Example with SM3

Problem Statement

For:
    34 x1  + 30 x2  + 37 x3  ≤  888
    11 x1  + 2 x2  + -15 x3  ≤  33
    16 x1  + -9 x2  + 2 x3  ≥  48
    14 x1  + 74 x2  + -31 x3  ≥  304
    Maximize:   -8 x1  + 4 x2  + 14 x3

Create the Initial Tableau

After reconfiguring the objective function and converting any '≥' constraints to a '≤' form, we can produce the following tableau:
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   34   30   37   1   0   0   0   0   888 
 s2   11   2   -15   0   1   0   0   0   33 
 s3   -16   9   -2   0   0   1   0   0   -48 
 s4   -14   -74   31   0   0   0   1   0   -304 
   8   -4   -14   0   0   0   0   1   0 

We can do this with the TI-83 calculators and the SM3 program. Although the program will allow us to enter a base matrix to represent the constraints, it is easier to construct a temporary matrix first and then give SM3 the name of the matrix when it is needed. For this example, we will create the basic matrix in matrix [A] using the matrix editor. The basic matrix has a row for every constraint and a column for every variable along with one for the constants in the inequalities. However, the SM3 program assumes that all inequalities have been converted to ≤ type inequalities. Thus, we need to rewrite the inequalities as
    34 x1  + 30 x2  + 37 x3  ≤  888
    11 x1  + 2 x2  + -15 x3  ≤  33
    -16 x1  + 9 x2  + -2 x3  ≤  -48
    -14 x1  + -74 x2  + 31 x3  ≤  -304
Below is a slightly doctored screen image from a TI-84 showing the matrix in the matrix editor. (The "doctoring" is the result of pasting together multiple imaages taken as one scrolls across the tiny TI-84 screen.)
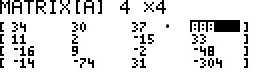and, from another perspective, here is the normal display of the matrix.
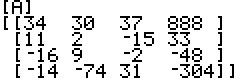Starting the SM3 program, it clears the screen, asks for the number of variables (we have 3 in this problem), the number of constraints (there are 4 inequalities), and then the matrix holding the coefficients of the variables and the constants for the constraints. Here is a screen shot of the openning interaction from the SM3 program with the user input highlighted.
Notice that we were able to just give the name of the constraint matrix rather than having to enter it in at this point.

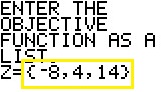
The SM3 program now needs the coeeficients of the variables for the objective function. In this case we need to enter the coeeficients, in the right order, as part of a list, as shown in:

The next question from the SM3 program relates to the choice between finding the maximum or minimum. The prompt and the user response are on the following screen:

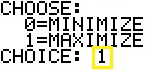At this point the SM3 program can actually construct the initial tableau. The TI-84 version of that tableau is given as:
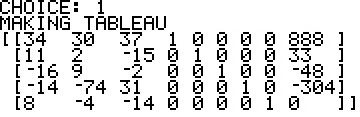The SM3 now does the next few steps in the Simplex Method to first decide that preprocessing is needed, because there are negative values in the last column, second to determine the work row, the row with the most negative value in the final column, and third the work column, the column with the most negative value in the work row. This web page goes through those steps one at a time. We can follow the web page until we catch up with the SM3 program.

Preprocessing

There is at least one negative value in the last column (excluding the final row). Therefore we need to start the preprocessing algorithm.

Lowest negative value in the last column is -304 and that is in row 4. So make row 4 the work row.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   34   30   37   1   0   0   0   0   888 
 s2   11   2   -15   0   1   0   0   0   33 
 s3   -16   9   -2   0   0   1   0   0   -48 
 s4   -14   -74   31   0   0   0   1   0   -304 
   8   -4   -14   0   0   0   0   1   0 

Lowest negative value in the row 4 is -74 and that is in column 2. So make column 2 the work column. That makes the item in row 4 and column 2 the pivot item.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   34   30   37   1   0   0   0   0   888 
 s2   11   2   -15   0   1   0   0   0   33 
 s3   -16   9   -2   0   0   1   0   0   -48 
 s4   -14   -74   31   0   0   0   1   0   -304 
   8   -4   -14   0   0   0   0   1   0 

The SM3 program arrives at this point of the process and displays:

Once we press the ENTER key on the calculator, the SM3 program will first use the *row operation to make the pivot hold the value 1 and then use the *row+ operation to make the 0 value in the rest of that column. This web page shows the entire process below; we will resume tracing the SM3 program after a few steps.

Use the elementary row operation *row to change the pivot item to be 1. That is, multiply row 4 by -1 / 74.

   x1   x2   x3   s1   s2   s3   s4   z   
 s1   34   30   37   1   0   0   0   0   888 
 s2   11   2   -15   0   1   0   0   0   33 
 s3   -16   9   -2   0   0   1   0   0   -48 
 s4   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   8   -4   -14   0   0   0   0   1   0 
Now use the elementary row operation *row+ to change the other items in column 2 to 0.
  1. multiply row 4 by -30 and add to row 1.
  2. multiply row 4 by -2 and add to row 2.
  3. multiply row 4 by -9 and add to row 3.
  4. multiply row 4 by 4 and add to row 5.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   1048/37   0   1834/37   1   0   0   15/37   0   28296/37 
 s2   393/37   0   -524/37   0   1   0   1/37   0   917/37 
 s3   -655/37   0   131/74   0   0   1   9/74   0   -3144/37 
 s4   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   324/37   0   -580/37   0   0   0   -2/37   1   608/37 
Now we need to copy the heading for the work column (column 2) to the heading for the work row (row 4).
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   1048/37   0   1834/37   1   0   0   15/37   0   28296/37 
 s2   393/37   0   -524/37   0   1   0   1/37   0   917/37 
 s3   -655/37   0   131/74   0   0   1   9/74   0   -3144/37 
 x2   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   324/37   0   -580/37   0   0   0   -2/37   1   608/37 
The SM3 program jumps from telling us the location of the pivot point to showing us the results of using that pivort point:
Note that these are exactly the values from the last tableau on the web page. The SM3 program, after we press the ENTER key, looks at the last column, determines that there is more preproccing to do, finds the most negative value in the final column, sets tht row as the work row, finds the most negative value in that row, sets that location as the pivot location, and then tells us all about its efforts. However, we will wait for the web page to get to that point before we look at the next output from SM3.
Having finished the steps of the preprocessing routine, we need to see if there are any remaining negative values in the final column. If so, then we restart the preprocessing steps.

Lowest negative value in the last column is -3144 / 37  = -84.972972972973 and that is in row 3. So make row 3 the work row.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   1048/37   0   1834/37   1   0   0   15/37   0   28296/37 
 s2   393/37   0   -524/37   0   1   0   1/37   0   917/37 
 s3   -655/37   0   131/74   0   0   1   9/74   0   -3144/37 
 x2   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   324/37   0   -580/37   0   0   0   -2/37   1   608/37 

Lowest negative value in the row 3 is -655 / 37  = -17.7027027027027 and that is in column 1. So make column 1 the work column. That makes the item in row 3 and column 1 the pivot item.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   1048/37   0   1834/37   1   0   0   15/37   0   28296/37 
 s2   393/37   0   -524/37   0   1   0   1/37   0   917/37 
 s3   -655/37   0   131/74   0   0   1   9/74   0   -3144/37 
 x2   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   324/37   0   -580/37   0   0   0   -2/37   1   608/37 
Here is the SM3 presentation of the same information:
As before, the web page walks us through the steps, but the SM3 program moves to display the tableau.
Use the elementary row operation *row to change the pivot item to be 1. That is, multiply row 3 by -37 / 655.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   1048/37   0   1834/37   1   0   0   15/37   0   28296/37 
 s2   393/37   0   -524/37   0   1   0   1/37   0   917/37 
 s3   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   7/37   1   -31/74   0   0   0   -1/74   0   152/37 
   324/37   0   -580/37   0   0   0   -2/37   1   608/37 
Now use the elementary row operation *row+ to change the other items in column 1 to 0.
  1. multiply row 3 by -1048 / 37 and add to row 1.
  2. multiply row 3 by -393 / 37 and add to row 2.
  3. multiply row 3 by -7 / 37 and add to row 4.
  4. multiply row 3 by -324 / 37 and add to row 5.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   262/5   1   0   8/5   3/5   0   3144/5 
 s2   0   0   -131/10   0   1   3/5   1/10   0   -131/5 
 s3   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   0   1   -2/5   0   0   7/655   -8/655   0   16/5 
   0   0   -74/5   0   0   324/655   4/655   1   -128/5 
Now we need to copy the heading for the work column (column 1) to the heading for the work row (row 3).
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   262/5   1   0   8/5   3/5   0   3144/5 
 s2   0   0   -131/10   0   1   3/5   1/10   0   -131/5 
 x1   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   0   1   -2/5   0   0   7/655   -8/655   0   16/5 
   0   0   -74/5   0   0   324/655   4/655   1   -128/5 
The calculator display at this point is
Again, the values match.
Having finished the steps of the preprocessing routine, we need to see if there are any remaining negative values in the final column. If so, then we restart the preprocessing steps.

Lowest negative value in the last column is -131 / 5  = -26.2 and that is in row 2. So make row 2 the work row.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   262/5   1   0   8/5   3/5   0   3144/5 
 s2   0   0   -131/10   0   1   3/5   1/10   0   -131/5 
 x1   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   0   1   -2/5   0   0   7/655   -8/655   0   16/5 
   0   0   -74/5   0   0   324/655   4/655   1   -128/5 

Lowest negative value in the row 2 is -131 / 10  = -13.1 and that is in column 3. So make column 3 the work column. That makes the item in row 2 and column 3 the pivot item.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   262/5   1   0   8/5   3/5   0   3144/5 
 s2   0   0   -131/10   0   1   3/5   1/10   0   -131/5 
 x1   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   0   1   -2/5   0   0   7/655   -8/655   0   16/5 
   0   0   -74/5   0   0   324/655   4/655   1   -128/5 
Here is the program display of the same information:
Use the elementary row operation *row to change the pivot item to be 1. That is, multiply row 2 by -10 / 131.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   262/5   1   0   8/5   3/5   0   3144/5 
 s2   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   -1/10   0   0   -37/655   -9/1310   0   24/5 
 x2   0   1   -2/5   0   0   7/655   -8/655   0   16/5 
   0   0   -74/5   0   0   324/655   4/655   1   -128/5 
Now use the elementary row operation *row+ to change the other items in column 3 to 0.
  1. multiply row 2 by -262 / 5 and add to row 1.
  2. multiply row 2 by 1 / 10 and add to row 3.
  3. multiply row 2 by 2 / 5 and add to row 4.
  4. multiply row 2 by 74 / 5 and add to row 5.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1   4   4   1   0   524 
 s2   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   0   0   -1/131   -8/131   -1/131   0   5 
 x2   0   1   0   0   -4/131   -1/131   -2/131   0   4 
   0   0   0   0   -148/131   -24/131   -14/131   1   4 
Now we need to copy the heading for the work column (column 3) to the heading for the work row (row 2).
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1   4   4   1   0   524 
 x3   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   0   0   -1/131   -8/131   -1/131   0   5 
 x2   0   1   0   0   -4/131   -1/131   -2/131   0   4 
   0   0   0   0   -148/131   -24/131   -14/131   1   4 
Here is the SM3 version of the tableau.
Having finished the steps of the preprocessing routine, we need to see if there are any remaining negative values in the final column. If so, then we restart the preprocessing steps.
There are no more negative values is the final column. Therefore, preprocessing is done...

The SM3 program announces the same thing as:
followed by another display of the tableau:

Processing

There is at least one negative value in the last row (excluding the final column). Therefore we need to start the regular simplex processing algorithm.

Lowest negative value in the last row is -148 / 131  = -1.12977099236641 and that is in column 5. So make column 5 the work column.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1   4   4   1   0   524 
 x3   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   0   0   -1/131   -8/131   -1/131   0   5 
 x2   0   1   0   0   -4/131   -1/131   -2/131   0   4 
   0   0   0   0   -148/131   -24/131   -14/131   1   4 

Lowest ratio in the column 5 is 131 and that is in row 1. So make row 1 the work row. That makes the item in row 1 and column 5 the pivot item.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1   4   4   1   0   524 
 x3   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   0   0   -1/131   -8/131   -1/131   0   5 
 x2   0   1   0   0   -4/131   -1/131   -2/131   0   4 
   0   0   0   0   -148/131   -24/131   -14/131   1   4 
The program displays the same information as
Use the elementary row operation *row to change the pivot item to be 1. That is, multiply row 1 by 1 / 4.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1/4   1   1   1/4   0   131 
 x3   0   0   1   0   -10/131   -6/131   -1/131   0   2 
 x1   1   0   0   0   -1/131   -8/131   -1/131   0   5 
 x2   0   1   0   0   -4/131   -1/131   -2/131   0   4 
   0   0   0   0   -148/131   -24/131   -14/131   1   4 
Now use the elementary row operation *row+ to change the other items in column 5 to 0.
  1. multiply row 1 by 10 / 131 and add to row 2.
  2. multiply row 1 by 1 / 131 and add to row 3.
  3. multiply row 1 by 4 / 131 and add to row 4.
  4. multiply row 1 by 148 / 131 and add to row 5.
   x1   x2   x3   s1   s2   s3   s4   z   
 s1   0   0   0   1/4   1   1   1/4   0   131 
 x3   0   0   1   5/262   0   4/131   3/262   0   12 
 x1   1   0   0   1/524   0   -7/131   -3/524   0   6 
 x2   0   1   0   1/131   0   3/131   -1/131   0   8 
   0   0   0   37/131   0   124/131   23/131   1   152 
Now we need to copy the heading for the work column (column 5) to the heading for the work row (row 1).
   x1   x2   x3   s1   s2   s3   s4   z   
 s2   0   0   0   1/4   1   1   1/4   0   131 
 x3   0   0   1   5/262   0   4/131   3/262   0   12 
 x1   1   0   0   1/524   0   -7/131   -3/524   0   6 
 x2   0   1   0   1/131   0   3/131   -1/131   0   8 
   0   0   0   37/131   0   124/131   23/131   1   152 
The program displays the tableau at this point as
Having finished the steps of the preprocessing routine, we need to see if there are any remaining negative values in the final column. If so, then we restart the preprocessing steps.
There are no more negative values is the final column. Therefore, regular processing is done...
The program announces the end of the process:

Display the answers.

Note that if a variable does not appear in the following list then it should be given the value 0. The list is generated from the final tableau by reading down the labels on the left and assigning to each the value in the rightmost column. Any slack variables in the labels of the left will be included in the list, but they can be ignored.
When the objective function has a Maximum = 152
The SM3 presents the solution as
followed by yet another display of the tableau
and, at the very end, an indication that it is DONE:

©Roger M. Palay     Saline, MI 48176     October, 2010