Sets

Links to section headings

Definition

Set Membership

Set Listing, Infinite Sets, and Set Builder Notation

Subsets, Supersets, Proper Subsets, and Set Equality

Union

Intersection

The Empty Set or Null Set

Set Complement

A small recap on topics

The Distributive Property

Definition (top)

Sets have a special meaning in mathematics, a little different from what we might mean in ordinary spoken and written language. In particular, a set in mathematics is just a collection of "things" but with the understanding that:

no item in the collection is repeated; and
the order in which items appear does not make any difference.

We often list the items of a set by writing them between "squiggly braces" and separated by commas. Thus we might have a set such as {big, red, one, five, bird} Furthermore, we often give sets a name, generally a capital letter. So we might say G = {big, red, one, five, bird} We note that each if the items in the set is unique. Furthermore, we could have said, G = {one, big, five, bird, red} and we would have described the same set. In fact, if we were told that H = {big, bird, five, one, red} then we could correctly declare that H = G because H and G are exactly the same set (remember that the order of the things in a set is immaterial.

Set Membership (top)

In the set H given above, we see that "bird" is one of the things in the set. We use the symbol "∈" to mean "is in the set", or "is a member of the set", or "is an element of the set" or "is in the set". Thus we could write bird ∈ H [Unfortunately, we often get quite sloppy in how we write ∈; some times it is written as ε and other times it appears as

.] Just as we use ∈ to mean "is in", we use ∉ to mean "is not in", or "is not a member of" or "is not an element of" or "is not contained in".

In an effort to make this page a bit more helpful, many of the following sets are created anew each time this page is loaded. Thus, when the page is reloaded you will find that the sets have changed and as such the examples change, thus providing you with new examples of the points being illustrated.

Below is a table with four rows. Each row contains a definition for a set. Each row also contains examples of "things" that are either "in" or "not in" the set for that row.

Set Listing, Infinite Sets, and Set Builder Notation (top)

As noted above, we often specify a set by listing its members, in any order, where we place the elements between squiggly braces and we separate the elements of the set by using commas. Consider the set A = } This is the set of the whole numbers between 1 and 17 inclusive, although we might not recognize this just looking at such an unordered list of numbers. On the other hand, we might write an equal set such as B = { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17} recognizing that for these two sets A = B. It is clearly easier to recognize the elements of this second listing than it was to check out the elements of the first set A. We can shorten the listing by taking advantage of the fact that we can actually recognize a pattern to the elements in the set. We do this by listing some elements until a pattern is recognizable, then we place an ellipsis (three dots in a row, as in ...) to represent some un-shown elements of the set, and we conclude the listing with the ending elements of the set. Thus, we could write a third version of our set as C = { 1, 2, 3, 4, ..., 16, 17} All three sets, A, B, C, have exactly the same elements so A=B=C.

When we use an ellipsis to show that we are "implying some unlisted elements" of the set we must be sure that we have established a clear pattern for the set. Consider two more examples. First we have the set D given as

D = {11, 18, 25, 32, ..., 81, 88} Here we see that we start with 11 and that we increase by 7 for each subsequent element in the set. If we had to we could expand the listing to D = {11, 18, 25, 32, 39, 46, 53, 60, 67, 74, 81, 88} so that we can "see" all of the elements of the set. Sometimes the "pattern" is not so easy to see. We need to be sure that we give the reader enough information to correctly identify the pattern. A less obvious pattern might be E = {3, 13, 23, 30, 31, 32, 34, 35, 36, 37, 38, 39, 43, 53, ..., 293, 300, 301, 302, 304} This almost looks like a "riddle" until we note that each element of the set has exactly one "3" in it, and that the lowest value is 3 and the highest value is 304. Applying that pattern we could observe that 138 ∈ E, 133 ∉ E, 204 ∉ E, and 234 ∈ E.

All of the sets so far have been "finite" sets. It has been possible, though perhaps inconvenient, to list all of the elements of the set. Even a really large finite set can be specified as a listing. Thus, we could have the set recognizing that F = G for those sets.

However, there is nothing that says a set must be finite. We could have the set

H = which uses the same pattern as did sets F and G but set H does not stop. The pattern just keeps going. Therefore,

In the previous examples we have used the initial elements in the listing of the set to set the pattern. This need not be the case. We could just as easily have used the final elements in the set listing to demonstrate the pattern. For example, we could have constructed the set

We can use the same technique to have a set listing for an infinite set where the set listing starts with the ellipsis. For example, consider the set

K = { ...

Besides "listing" the elements of a set, we also have a way to just specify the "rule" that we will use to determine if something is or is not an element of the set. We do this via the "set builder" notation. For example, we could write You might have noticed that in set N we specified x ∈ Z rather than just saying x. We did this so that it was clear that we were only interested in integer values. We could have put that restriction on either side of the vertical bar. Thus, we could have just as easily specified set N as In set builder notation it is important to specify a rule that allows the reader to determine whether or not something is or is not an element of the set.

Subsets, Supersets, Proper Subsets, and Set Equality (top)

Table I

Earlier we noted that we often use capital letters to name sets. As a consequence, we find ourselves reusing those letters for different sets. The examples given above have served their purpose. Starting at here we have new sets to consider. They are

A = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
B = { 4, 5 }
C = { 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
D = { 7, 8 }
E = { 12, 13, 14 }
F = { 12, 13, 14 }
G = { 11, 12, 13, 14 }

Looking at those sets we note that "every element of B is also an element of A. In such a situation we say that B is a subset of A. We even have a symbol to represent "is a subset of" and that symbol is ⊆. Therefore, we write B ⊆ A. In fact, for the sets given in Table I above,

B ⊆ A
D ⊆ A
D ⊆ C
E ⊆ C
F ⊆ C

G ⊆ C
E ⊆ G
F ⊆ G
E ⊆ F
F ⊆ E

The last two on the right of these, E ⊆ F and F ⊆ F, may seem a bit strange. However, they both meet the definition of "is a subset of", namely, to say E ⊆ F we need every element of E to be an element of F, and to say F ⊆ E we need every element of F to be an element of E. Both are true. From our earlier work we can look at sets E and F and we can give the stronger statement that E = F, but the individual weaker statements are also true.

Interestingly enough, we can read the statement B ⊆ A backwards, that is right to left, as "A is a superset of B", meaning that A contains all of the elements of B. Just to make life a bit more complicated we have a different symbol, ⊇ that can be read left to right as "is a superset of", as in A ⊇ B, or we can read that right to left as B is a subset of A.

We note that both E ⊆ F and E ⊆ G are true. However, we should be able to differentiate these cases in that G has at least one element, in our example that is 11, that is not in E. In particular, we have that 11∈G but 11∉E. We make such a differentiation by saying "E is a proper subset of G". We even have a symbol, ⊂, to express "is a proper subset of". Thus, when we say B ⊂ A we mean that every element of B is also an element of A and A has at least one element that is not an element of B.

For a moment, let us return to the case of sets E and F. We know that all three of the following statements are true:

E = F
E ⊆ F
F ⊆ E

We also know how to prove the last two of those statements (we just need to show that if an element is in the set of the left of ⊆ then it is in the set on the right of ⊆. Because we know how to prove these last two statements, we are often in the position where, in order to prove the first statement, the equality, we just prove both of the last two statements. An example of such a proof is given below.

Union (top)

In this section we want to consider the binary operation on sets called union and intersection. The union of two sets is a new set formed by combining all of the elements of the original sets, remembering that we do not repeat elements in a set. The symbol for union is ∪. Thus, for the set D = { 7, 8 } given in Table I along with a new set H = { 6, 7, 15 }, we could take the statement "the union of sets D and H" and write it as D ∪ H. Looking at the sets we can see that D ∪ H= { 6, 7, 8, 15} because those are exactly the elements that are found in one, the other, or both of the two sets D and H. This would be a good time to use our set builder notation. For any two sets S and T we have that S ∪ T= { x | x∈S or x∈T } The or in that notation is the inclusive "or" meaning that something could be in either one of the two sets or in both S and T and it will still be in the union of the two sets. That is exactly what happened in our example where 7 ∈ D and 7 ∈ H. We have that 7 ∈ D ∪ H.

As a small aside, in English we often use the word "or" in an exclusive sense. For example, when shopping with my young son I might say, "you can have a candy bar or an ice cream bar." We all understand that such a statement is not an offer to have both of them. That is an "exclusive or", and in mathematics we write that as "xor" to differentiate it from the "inclusive or" which we write as "or".

There are some "properties of union that we should address. First, union is commutative. That means that for any two sets S and T, we have S ∪ T = T ∪ S We can use the earlier discussion about proving set equality to both prove this and to demonstrate the method of proof. To some people it is interesting to see this kind of proof. It is a bit pedantic but it does exemplify how we prove set equality.

Proof that S∪T = T∪S
Part I: show that S∪T ⊆ T∪S Let x ∈ S∪T, then there are three possible cases:
Case I: x ∈ S but x ∉ T	Case II: x ∉ S but x ∈ T	Case I: x ∈ S and x ∈ T
then x ∈ S so x ∈ T∪S Therefore, S∪T ⊆ T∪S	then x ∈ T so x ∈ T∪S Therefore, S∪T ⊆ T∪S	then x ∈ S so x ∈ T∪S Therefore, S∪T ⊆ T∪S
Conclusion of Part I: in all cases S∪T ⊆ T∪S
Part II: show that T∪S ⊆ S∪T Let x ∈ T∪S, then there are three possible cases:
Case I: x ∈ S but x ∉ T	Case II: x ∉ S but x ∈ T	Case I: x ∈ S and x ∈ T
then x ∈ S so x ∈ S∪T Therefore, T∪S ⊆ S∪T	then x ∈ T so x ∈ S∪T Therefore, T∪S ⊆ S∪T	then x ∈ S so x ∈ S∪T Therefore, T∪S ⊆ S∪T
Conclusion of Part II: in all cases T∪S ⊆ S∪T
We have shown that S∪T ⊆ T∪S and T∪S ⊆ S∪T , therefore S∪T = T∪S

A second property is that union is associative. That means that for any three sets, R, S, and T we have R∪S∪T = (R∪S)∪T = R∪(S∪T)

The following table, Table II, gives us some new sets to consider. The table goes on to give us examples of finding the union of each pair of sets. The elements of each set change whenever this page is reloaded.

Intersection (top)

Intersection, represented by the symbol ∩, takes two sets and produces a new set where the elements of the new set have to appear in both of the original sets. Thus, for the set D = { 7, 8 } given in Table I along with a new set H = { 6, 7, 15 }, we could take the statement "the intersection of sets D and H" and write it as D ∩ H. Looking at the sets we can see that D ∩ H= { 7 } because that is the set of all elements that are in both sets D and H. This would be a good time to use our set builder notation. For any two sets S and T we have that S ∩ T= { x | x∈S and x∈T } We should note here that union, represented by ∪, corresponds to our word or (that is, the inclusive "or") whereas intersection, represented by ∩, corresponds to our word and. Furthermore, the two properties that we saw before, the associative and commutative properties, also apply to the operation of intersection. Thus, for any two sets S and T, we have S ∩ T = T ∩ S , the commutative property for intersection and, for any three sets, R, S, and T we have R∩S∩T = (R∩S)∩T = R∩(S∩T) , the associative property for intersection

The Empty Set or Null Set (top)

When we look at sets B = {4,5} and E={7,8) from Table I, we can constuct the intersection of the two sets as B∩E. When we look at B∩E we realize that there are no elements in that new set, thus B∩E = { } The set { } has not just one but two special names, namely, it is called the empty set and it is called the null set. Furthermore, we have a special symbol for this set, namely, ∅. The two names, empty and null, and the two symbols { } and ∅ are interchangeable.

A word of caution. One of the more common "trick" questions is to falsely suggest {∅} is the empty set. Remember that a set is a collection of "things". One such "thing" could be the empty set. This, the set {∅} is the set that contains one thing and that one thing is the empty set. Since the empty set has nothing in it and the set {∅} has one thing in it, the two sets are not identical. We would write this as {∅} ≠ ∅ We can carry this even further. Look at the yet another set, { ∅, {∅} }. This strange looking set has two elements, one being the empty set and the other being the set that has one element where that one element is the empty set.

We have a special term for sets whose intersection is the empty set. We call such sets disjoint. Thus, if we have two sets, S and T and we are told that S and T are disjoint then we know that S ∩ T = ∅. Likewise, if we are told that S ∩ T = ∅ then we call S and T disjoint.

The empty set has a special relation with the operation of union, namely, the result of the union of any set and the empty set is that original set. Using symbols, we say that for any set T

T ∪ ∅ = T = ∅ ∪ T We notice that the relation of the empty set to union is similar to the relation of the number 0 to the operation of addition, or the relation of the number 1 to the operations of multiplication. Note that for any number x we have x + 0 = x 0 + x
x × 1 = x = 1 × x Such a relation makes 0 the identity element for the operation of addition, 1 the identity element for the operation of multiplication, and ∅ the identity element for the operation of union.

Set Complement (top)

This does give us a moment of thought. Since ∅ is the identity element for the operation of union, is there an identity element for the operation of intersection? In symbolds, if we have any set T is there some set which we will call M such that

T ∩ U = T= U ∩ T In order to answer this, we need to introduce a new set called the universal set. Unfortunately, there is no one universal set. Rather, for any problem on which we are working, we need to define a specific universal set. For example, if we are looking at problems related to the sets given in Table I above, then we might want to define the universal set for our problems as the set U = { 1, 2, 3, 4, ..., 14, 15 } This would be the "smallest" universal set that we could define for any problems using the sets in Table I above because this is the set of all the elements that are in those sets. Once we have such a definition, then that universal set fullfills the requirement T ∩ U = T= U ∩ T for any set T that appears in Table I.

Having defined that universal set, it is essential that we realize that we could have defined a different universal set, say,

U = { 0, 1, 2, 3, 4, ..., 14, 15, 16, 17 } If we made this alternative definition, then the newly defined universal set acts as the identity element for the operation of intersection for all of the sets in Table I.

Let us continue this discussion using the sets of Table I and the universal set defined as

U = { 0, 1, 2, 3, 4, ..., 14, 15, 16, 17 } With that understanding, we can introduce a new operation, the complement operation. Unlike union and intersection, the complement operation is a unary operation. That means that it acts a single set to produce a result, a new set. Union and intersection are binary operations because they act on two sets to produce a result. The complement of a set is the set of all elements that are in the universal set but that are not in the set for which we are finding the complement. We actually have two popular ways to show the complement operation: for a set T we can symbolize the complement of T as either T^' or T^c. In symbols we would write T^' = T^c = {x∈U | x∉T } Note that in order for us to identify the complement of a set we must know the universal set that we are using. Thus, if the universal set is U = { 0, 1, 2, 3, 4, ..., 14, 15, 16, 17 } we can form the complement of each of the sets in Table I, repeated below in Table III, as

Table III

A repeat of Table I with the understanding that the universal set is U = { 0, 1, 2, 3, 4, ..., 14, 15, 16, 17 } and giving the complement of each set.

A = { 1, 2, 3, 4, 5, 6, 7, 8, 9 }
B = { 4, 5 }
C = { 6, 7, 8, 9, 10, 11, 12, 13, 14, 15 }
D = { 7, 8 }
E = { 12, 13, 14 }
F = { 12, 13, 14 }
G = { 11, 12, 13, 14 }

A^'= { 0, 10, 11, 12, 13, 14, 15, 16, 17 }
B^'= { 0, 1, 2, 3, 6, 7, 8, 9, 10, 11, 12, 13, 14, 15, 16, 17 }
C^'= { 0, 1, 2, 3, 4, 5, 16, 17 }
D^'= { 0, 1, 2, 3, 4, 5, 6, 9, 10, 11, 12, 13, 14, 15, 16, 17 }
E^'= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15, 16, 17 }
F^'= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11, 15, 16, 17 }
G^'= { 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 15, 16, 17 }

A small recap on topics (top)

Here is a new table with some new sets along with some operations (and the sets resulting from those operations) for these new sets.

The Distributive Property (top)

Earlier we noted both the commutative and associative properties of both union and intersection. We also have the distributive property to consider. Recall that for numbers we have the property that multiplication distributes over addition. Thus, for example, using numbers we have 5(6 + 8) = 5(6) + 5(8) or using the symbols, a, b, and c as numbers, it is always true that a(b + c) = a(b) + a(c). Interestingly, for sets we have both the property that union distributes over intersection and the property that intersection distributes over union. The former case means that for any three sets R, S, and T, it is always true that R ∪ ( S ∩ T ) = (R ∪ S) ∩ (R ∪ T ) while the latter means that for any such sets it is always true that R ∩ ( S ∪ T ) = (R ∩ S) ∪ (R ∩ T )

More on the Complement (top)

Once we have the ideas of the complement of a set, the union of two sets, and the intersection of two sets, we have two more interesting relationships, namely, the complement of a union is the intersection of the complements, and the complement of an intersection is the union of the complements. In symbols, for two sets S and T, it is always true that (S ∪ T)^' = S^' ∩ T^' and it is also always true that (S ∩ T)^' = S^' ∪ T^'

Venn Diagrams (top)

Although we could prove all four of the last "properties", it is often easier to understand them through pictures. Venn diagrams give us a way to "picture" the relationship between sets. For a Venn diagram we start with a rectangle to represent our universal set, as in

Then, we represent a set, we will call it A, within that universal set as a circle, and we label that circle. Thus, to represent the set A we draw

The size of the circle, and even the location of the circle are meaningless in a Venn diagram. However, when we add another set to the picture we need to do so in such a way that the picture represents the relation of the two sets. Thus, if we have

Table V new set definitions to use below

U = { 1, 2, 3, ..., 23, 24, 25 }
A = { 1, 2, 3, 4, 5, 6, 7, 8 }
B = { 3, 4, 5, 6, 9, 10, 11, 12 13, 14 }
C = { 5, 6, 7, 14, 15, 16, 17 }
D = { 18, 19, 20, 21 }
E = { 11, 12 }

and we want to have a Venn diagram for sets A and B, then we need to show in that diagram that A and B overlap, having elements 3, 4, 5, and 6 in common, but that they have other values that are unique to the two sets. We would draw this as

Here we can see that the two circles do overlap but that they have areas that are unique to themselves. Again, the size of the overlap and the size of the regions inside the circles but outside the overlap is immaterial. The Venn diagram merely shows the relation between the sets. We could complete the diagram for all five sets given in Table V as

Here we note that D has no overlap with any of the other sets. Also set E is entirely within set B but completely outside of either set A or set C. Furthermore, set C is drawn to show that it overlaps both set A and set B, having at least one element (namely, 7) in common with A but not B, at least one element (namely 14) in common with B but not A, at least one element (namely, 5 and 6) in common with both A and B and having at least one element (namely, 15, 16, and 17) that are not in either A or B.

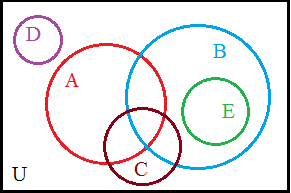
As noted above, we can use these Venn diagrams to "see" why a property such as

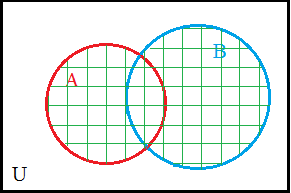
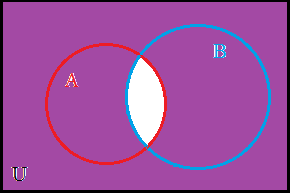
(S ∪ T)^' = S^' ∩ T^' is true. Let us use the two sets, A and B from Table V above to demonstrate this. Figure 1 gives the relationship of those two sets which we will rewrite as: (A ∪ B)^' = A^' ∩ B^'

Figure 1

Here is the Venn diagram of the sets A and B from Table V.

First, let us construct the left side of the equality, namely, (A ∪ B)^'. To do that we will start with just the union of the two sets.

Figure 2

The shaded portion of the image represents A ∪ B.

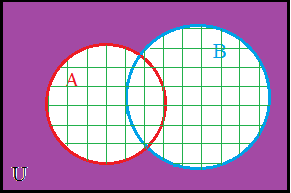
Then, the complement of that union is the region outside of the shaded portion.

Figure 3

The filled region represents the complement (A ∪ B)^'.

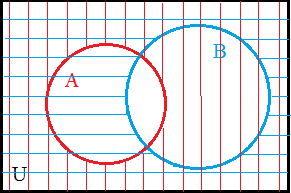
Now we turn our attention to the right side of the equation, namely, A^' ∩ B^'. Figure 4 shows the complement of A as the region shaded with vertical lines, and the complement of B as the region shaded with horizontal lines.

Figure 4

Shading both A^', via the region with vertical lines, and B^', via the region with horizontal lines.

Therefore, the intersection of the two complement areas is the region that has lines going both vertically and horizontally.

Figure 5

Filling in the region corresponding to A^' ∩ B^'.

Thus, Figure 3 represents the left side of the equation and Figure 5 represents the right side of the equation. As we can see by comparing the two figures, these are exactly the same regions in the Venn diagrams. That is, from the two figures, we can see that the equality (A ∪ B)^' = A^' ∩ B^' holds.

The other equality given above was

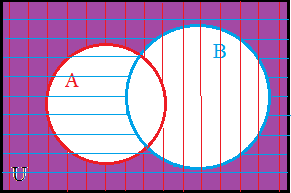
(S ∩ T)^' = S^' ∪ T^' To use the two sets A and B we restate this as (A ∩ B)^' = A^' ∪ B^' We can use a Venn diagram to illustrate the left side of the equality, that is (A ∩ B)^'

Figure 6

In this figure we have shaded set A with horizontal lines and set B with vertical lines. Thus, the doubly shaded region represents the intersection, (A ∩ B)

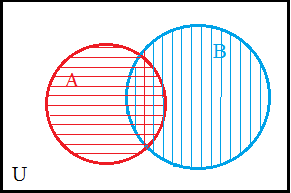
Figure 7 restates the intersection all by itself.

Figure 7

Here we look at just the intersection, (A ∩ B).

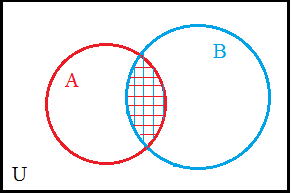
To identify the complement of the intersection we fill all of the rest of the diagram.

Figure 8

Here we have filled the rest of the diagram to indicate the region (A ∩ B)^'.

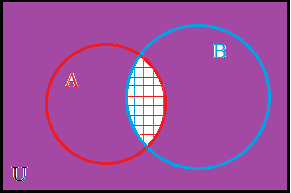
Now we can return to look at the left side of the equality, namely, A^' ∪ B^' To do this we first identify the two regions, A^' and B^' .

Figure 9

The complement of A is shaded with vertical lines and the complement of B is shaded with horizontal lines.

The union of A^' and B^' is the entire shaded region.

Figure 10

Filling all areas that were shaded in Figure 9 gives us te union of those two areas. Thus, Figure 10 represents A^' ∪ B^'.

Thus, the filled area of Figure 8 represents the left side of the equation and the filled area of Figure 10 represents the right side of the equation. As we can see by comparing the two figures, these are exactly the same regions in the Venn diagrams. That is, from the two figures, we can see that the equality (A ∩ B)^' = A^' ∪ B^' holds.

Set Cardinality (top)

Another aspect of sets is the size of the set, that is, the number of elements in the set. The number of elements in a set is called the cardinality of the set. The set S = { 3, ,7, 11, 23 } has 4 elements. Thus, we would say that the cardinality of set S is 4. [We take note here that our early "understanding: in the definition of a set made it clear that elements are either in a set or they are not, and, in particular, elements are not repeated in a set. This is required in order to clearly define cardinality.]

We have a way to indicate the cardinality of a set, namely,

the cardinality of set S is denoted as n(S).
To illustrate this, we will restate the sets of Table V in Table VI adding a column giving the cardinality of each of those sets.

Table VI
U = { 1, 2, 3, ..., 23, 24, 25 }	n(U) = 25
A = { 1, 2, 3, 4, 5, 6, 7, 8 }	n(A) =8
B = { 3, 4, 5, 6, 9, 10, 11, 12 13, 14 }	n(B) = 10
C = { 5, 6, 7, 14, 15, 16, 17 }	n(C) = 7
D = { 18, 19, 20, 21 }	n(D) = 4
E = { 11, 12 }	n(E) = 2

Using those sets we can investigate some deeper relations. For example, remembering that we have defined the universal set for the sets A through E in Table VI, we can look at the cardinality of the complement of a set. For example, the cardinality of the complement of set C is the number of elements that are in the complement of set C. The complement of set C is the set of all things in the universal set that are not in C. For the sets that we are using, C^' = { 1, 2, 3, 4, 8, 9, 10, 11, 12, 13, 18, 19, 20, 21, 22, 23, 24, 25 }
so we can see that n( C^' ) = 18
This suggests that we could write this relation as n( C^' ) = n( U ) – n( C )
Again, returning to our sets, we find that D ∪ E = { 11, 12, 18, 19 20 21 }
so we have n( D ∪ E ) = 6
When we consider that n( D ) = 4 and n( E ) = 2, we might jump to the incorrect conclusion that to find the cardinality of a union we can ~~find the sum of the the cardinalities of the two sets~~. Looking at A ∪ C shows a case where this clearly does not work. A ∪ C = ( 1, 2, 3, 4, 5, 6, 7, 8, 14, 15, 16, 17 }
n( A ) = 8
n( C ) = 7
n( A ∪ C ) = 12
and, 8 + 7 ≠ 12
If we examine the sets we are using we can see the problem here. The elements 5, 6 and 7 are in both A and C. Thus, when we find n( A ) = 8, that answer, 8, includes counting those three elements. When we find n( C ) = 7, that answer, 7, includes counting those three elements. However, those three elements appear only one time in A ∪ C. Therefore, when we find the cardinality of a union, it will be equal to the sum of the cardinalities of the two sets minus the cardinality of the set of elements that are common to both sets, that is, the intersection of the two sets. This, then, is a general rule that holds for any two sets n( S ∪ T ) = n( S ) + n( S ) – n( S ∩ T )
or, for our specific examples
n( A ∪ C ) = n( A ) + n( C ) – n( A ∩ C )
12 = 8 +7 – 3