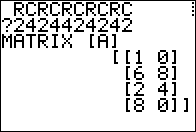
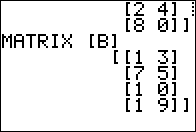
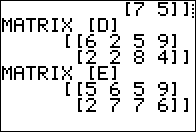
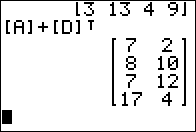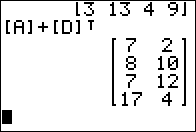Figure 01
|
5[A]+3[B]
|
Figure 02
|
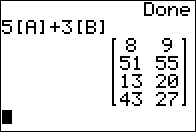
Both ([A]+[B])T
and [A]T+[B]T.
Notice that the results are identical. The general rule is that the
transpose of a sum of matrices is the the same as the sum of the
transposes of the matrices.
|
Figure 03
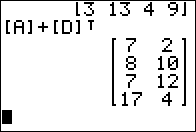
|
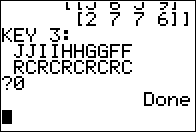
Although [A] and [D] do not have the same dimensions,
[A] and [D]T are both
4 x 3 matrices and therefore we can add them.
Note that this works because transpose has a higher precedence
than does addition. Therefore we need to
find the transpose of [D] before we add the two values.
|
Figure 04

|
Here is a slightly more complex version of
the same issue. We know that transpose has a higher precedence than
addition, and therefore a higher precedence than subtraction.
There is a question about the relation of transpose to scalar multiplication.
This example does not resolve that question. However, since scalar multiplication
can be thought of as a replacement for repeated addition, and because the "transpose of a sum is the same as the sum of the
transposes", we should get the same value for 2([C]T)
as we get for (2[C])T.
That means the relative precedence is unimportant.
|
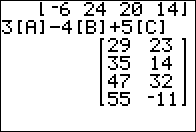
Figure 05
|
Figure 05 just demonstates a sightly more complex expression.
|
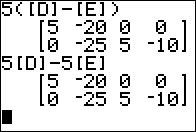
Figure 06
|
The two results shown in Figure 06 demonstrate that scalar multiplication
distributes over addition.
|