7 – 3 = 4
but 3 – 7 = –4.
&ndash1
times [B], store the result in [F]
and then have the calculator find [A]+[F] to get the same result that we had back in
Figure 01 with [A]ndash;[B].

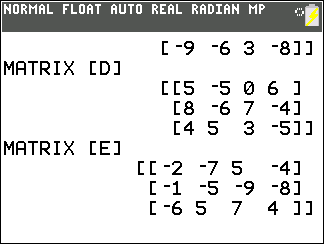
3 x 4 matrices as in
[D]–[E].
-8632501809
3434242424 and 0 to generate the
matrices:
5-3 we change that to
5 + –3; we change the subtraction
problem into an addition problem. In general, for numbers a and b,
the problem a - b becomes
a + –b.
Also, we understand that for numbers, in geneeral, we have that
–b = (–1) * b.
Our calculator does this same thing for matrix subtraction. That is, we interpret
[A] – [B] to be the same thing as
[A] + –[B]
which is the same as [A] + (–1)*[B].
In effect, we subtract matrices by subtrracting, in the proper order,
the correspondingelements of the two matrices. An example or two should make this
more concrete.
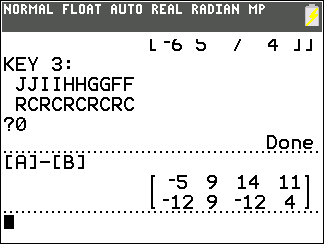
Figure 01 
|
|
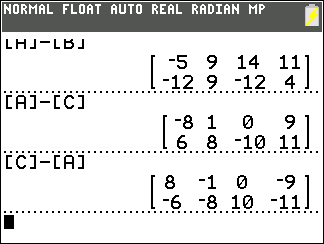
Figure 02 
|
Then we can look at [A]–[C] and at
[C]–[A], which give opposite results just as
7 – 3 = 4
but 3 – 7 = –4.
|
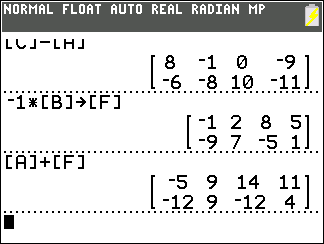
Figure 03 
|
Just to show that our disussion above holds, we can take &ndash1
times [B], store the result in [F]
and then have the calculator find [A]+[F] to get the same result that we had back in
Figure 01 with [A]ndash;[B].
|
Figure 04 
|
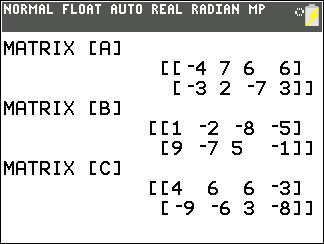
We finish this page with a small demonstration of
subtracting two 3 x 4 matrices as in
[D]–[E].
|