Matrix: Identity Matrices for Multiplication

Return to Roadmap 3

We can use the GNRNDM program with the same key values used in the matrix multiplication page, namely, the key values -6723101206, 4443244234 and 0000000033, to generate the matrices:

The calculator used to obtain the images below was a TI 84 Plus running the 2.55MP operating system and it was in the MATHPRINT display mode. These images merely reflect generating the matrices.

Our interest here is to find the particular matrices that will serve as the identity matrix for multiplication. This is similar to the recognizing that 1 ia the multiplicative identity value for numbers. We recognize that 1*4=4, and 4*1=4 as a particular case. In the same way, for any number a we now that 1*a=a=a*1.

We can start by looking at the particualr matrix and asking what matrix could we multiply times [A] and have the result be exactly [A]. An immediate problem presents itself here. We know that [A] is a 3 x 4 matrix. As a consequence, if we multiply a matrix on the left times [A] then that matrix will have to have 3 columns (so that the inside dimensions will match). Furthermore, if the result is to be a 3 x 4 matrix then the matrix on the left needs 3 rows (so that the outside dimensions become 3 and 4). That means the the left matrix must have 3 rows and 3 columns. It must be a 3 x 3 matrix.

On the other hand, if we are to multiply [A] times a matrix on its right then the that matrix will have to have 4 rows (so that the inside dimensions will match). Furthermore, if the result is to be a 3 x 4 matrix then the matrix on the right needs 4 columns (so that the outside dimensions become 3 and 4). That means the the right matrix must have 4 rows and 4 columns. It must be a 4 x 4 matrix.

Clearly, the same matrix cannot serve as both the identity on the left and the identity on the right.

Our 3 x 3 identity matrix is The figures and discussion below will walk us through creating and using these identity matrices on our TI-83/84 calculators.

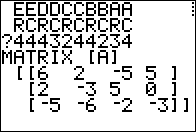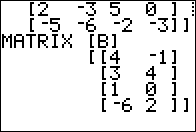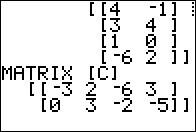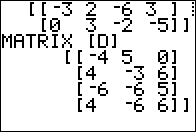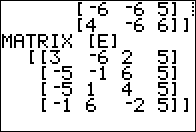
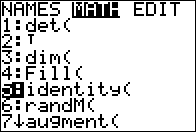
Figure 01	If we want to multiply the `3 x 3` identity matrix times [A], then the first thing we should do is to create that identity matrix. The TI-83/84 calculators have a built-in function,`identity(`, that does this. We move to the matrix window and then select the MATH option, and then move the highlight down to the desired item, as shown in Figure 01. Then we can press to paste that portion of a command onto the main screen.
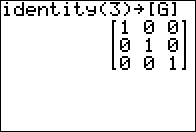
Figure 02	We complete the command by specifying the `3` to tell the calculator that we want to create a `3 x 3` identity matrix. Then we close the function with a right parenthesis and we will store the matrix in [G]. After creating the command we press to have the calculator perform it. The calculator then does the work and displays the new matrix.
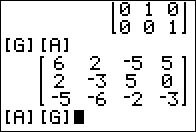
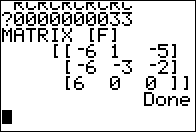
Figure 03	Toward the top of Figure 03 we see the command [G][A] telling the calculator to multiply [G] times [A]. It did this and displays the result, in Figure 03, which we can compare to the known value of [A] We see that the multiplication hasresuted in the same matrix that we started with, namely, [A]. Then, jsut as demonstration, we formulate, at the bottom of Figure 03, the command [A][G]. This should not work because [A] is a `3 x 4` matrix and [G] is a `3 x 3` matrix (the "inner" dimensions do not match). When we press `3 x 4` the calculator respondes with Figure 04.
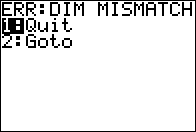
Figure 04	This is the expected error message. Press to Quit and return to the main screen.
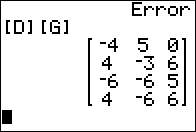
Figure 05	As long as we have our `3 x 3` identity matrix in [G] we can look at some other products. [D] is a `4 x 3` so we can multiply it on the right by [G].
Figure 06	[F] is a `43 x 3` so we can multiply it on the left or the right by [G]. Figure 06 shows the former.
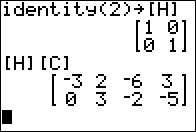
Figure 07	[C] is a `2 x 4` so we need a `2 x 2` identity to multiply it on the left. Figure 07 creates such an identity and puts it into [H]. Then it does the multiplication.
Figure 08	[B] is a `4 x 2` so we can multiply it on the right by [H].
Figure 09	In Figure 09 we replace the old [G] with a new `4 x 4` identity.
Figure 10	With that new identity we can multiply [A] on the right.
Figure 11	We can multiply [E] on the left.