Matrix: Definition
Return to Roadmap 3
A matrix is a rectangular arrangement of values. Those values can be
numbers as in
 or variables as in
or variables as in
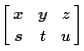 .
It is typical to give a matrix a name,
usually a bold capital letter, as in
.
It is typical to give a matrix a name,
usually a bold capital letter, as in
 .
However, the TI-83/84 family of calculators has a problem doing this.
On those calculators the uppercase letters are
already used as the names of simple variables.
Therefore, on those calcualtors we find that the
convention is to express the name inside square brackets, as in [A].
It is essential to note that what appears on the calculator screen to be a 3-character
symbol, is really just a single symbol. One cannot, on one of those calculators, type
the three characters [, A, and ] to produce the name
[A]. Rather, one must find the name of a matrix
in the matrix menu. More on that in a subsequent page.
.
However, the TI-83/84 family of calculators has a problem doing this.
On those calculators the uppercase letters are
already used as the names of simple variables.
Therefore, on those calcualtors we find that the
convention is to express the name inside square brackets, as in [A].
It is essential to note that what appears on the calculator screen to be a 3-character
symbol, is really just a single symbol. One cannot, on one of those calculators, type
the three characters [, A, and ] to produce the name
[A]. Rather, one must find the name of a matrix
in the matrix menu. More on that in a subsequent page.
A defining characteristic of a
matrix is its number of rows and columns. Thus the martix
 has 3 rows and 4 columns.
We say that it is a 3x4 matrix.
The matrix
has 3 rows and 4 columns.
We say that it is a 3x4 matrix.
The matrix
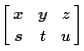 has 2 rows and
3 columns, so it is a 2 x 3 matrix.
The matrix
has 2 rows and
3 columns, so it is a 2 x 3 matrix.
The matrix  has 4 rows and 2 columns so it is a 4 x 2 matrix.
Here is an example of a larger matrix, one that changes each time this page
is loaded. This matrix has
has 4 rows and 2 columns so it is a 4 x 2 matrix.
Here is an example of a larger matrix, one that changes each time this page
is loaded. This matrix has
In general, a m x n has m rows and n columns;
the number of rows is always given first and the number of
columns is always given second.
A more general depiction of a matrix, in this case a 3 x 5 matrix
is given by
This shows that the item x24 is in
row 2, column 4. We use the same style to refer to a general element
of a matrix as element
xij, understanding that this
is the item in poistion
row i and column j of the matrix.
Return to Roadmap 3
©Roger M. Palay Saline, MI 48176 February, 2017
 or variables as in
or variables as in
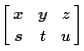 .
It is typical to give a matrix a name,
usually a bold capital letter, as in
.
It is typical to give a matrix a name,
usually a bold capital letter, as in
 .
However, the TI-83/84 family of calculators has a problem doing this.
On those calculators the uppercase letters are
already used as the names of simple variables.
Therefore, on those calcualtors we find that the
convention is to express the name inside square brackets, as in [A].
It is essential to note that what appears on the calculator screen to be a 3-character
symbol, is really just a single symbol. One cannot, on one of those calculators, type
the three characters [, A, and ] to produce the name
[A]. Rather, one must find the name of a matrix
in the matrix menu. More on that in a subsequent page.
.
However, the TI-83/84 family of calculators has a problem doing this.
On those calculators the uppercase letters are
already used as the names of simple variables.
Therefore, on those calcualtors we find that the
convention is to express the name inside square brackets, as in [A].
It is essential to note that what appears on the calculator screen to be a 3-character
symbol, is really just a single symbol. One cannot, on one of those calculators, type
the three characters [, A, and ] to produce the name
[A]. Rather, one must find the name of a matrix
in the matrix menu. More on that in a subsequent page.
 has 3 rows and 4 columns.
We say that it is a 3x4 matrix.
The matrix
has 3 rows and 4 columns.
We say that it is a 3x4 matrix.
The matrix
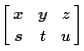 has 2 rows and
3 columns, so it is a 2 x 3 matrix.
The matrix
has 2 rows and
3 columns, so it is a 2 x 3 matrix.
The matrix  has 4 rows and 2 columns so it is a 4 x 2 matrix.
Here is an example of a larger matrix, one that changes each time this page
is loaded. This matrix has
has 4 rows and 2 columns so it is a 4 x 2 matrix.
Here is an example of a larger matrix, one that changes each time this page
is loaded. This matrix has