Figure 01
|
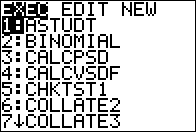
Open the PROGRAM menu by pressing the
 key. key.
|
Figure 02
|
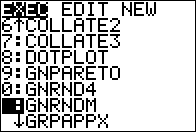
Use the  key to find and highlight
the GNRNDM program. Then press the key to find and highlight
the GNRNDM program. Then press the
 key to move to Figure 03. key to move to Figure 03.
|
Figure 03

|
Figure 03 shows the command needed to actually run the progrm.
We just need to press  to have the calculator
run the GNRNDM program to have the calculator
run the GNRNDM program
|
Figure 04
|
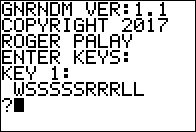
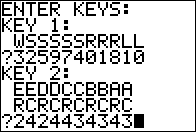
The program starts with a request for the value of the first key.
The program tries to convey the meaning of the key value: we have one
Wasted digit or symbol (explained later), 5 Seed value digits
for the random number generator, 3 Range digits, and 2 Start
digits. The program uses these to determine the lowest allowd value in the
matrix (SS) and the range of values allowed (RRR).Thus, the highest value in
the matrices will be LL+RRR. The Wasted value is ignored, unless it is a negative
sign, in which case the LL value is taken to be negative.
|
Figure 05
|
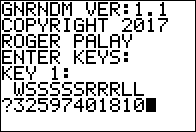
We respond, in Figure 05, with the value
322597401810, which means that the lowest value in the generated matrices is
10 and the highest is 28.
You might check the ten matrices shown above to verify that those limits
were in fact used.
Press  to move forward. to move forward.
|
Figure 06
|
The program prompts for the second key. This time the
program tries to help us by giving us the hint
EEDDCCBBAA
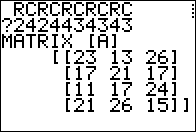
RCRCRCRCRC
to tell us that the two leftmost of the ten digits will specify
the number of rows and columns in matrix E, the next two digits will
specify the number of rows and columns in matrix D, and so on.
The response that we enter, 2424434343, specifies that
E is a 2x4, D is a 2x4, C is a 4x3, B is a 4x3,
and A is a 4x3.
Press  to give those values to the program. to give those values to the program.
|
Figure 07
|
The program starts to do its work. It creates and displays matrix A
and waits for us to press  to move on. to move on.
|
Figure 08

|
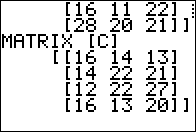
It creates and displays matrix B
and waits for us to press  to move on. to move on.
|
Figure 09
|
It creates and displays matrix C
and waits for us to press  to move on. to move on.
|
Figure 10
|
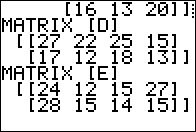
It creates and displays matrix D
and waits for us to press  to move on. Then
it creates and displays matrix E
and waits for us to press to move on. Then
it creates and displays matrix E
and waits for us to press  to move on. to move on.
|
Figure 11
|
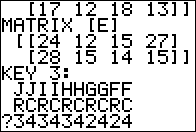
Now the program asks for the row and column sizes
of the last five matrices, J, I, H, G, and F.
Our response of 3434342424
specifies that
J is a 3x4, I is a 3x4, H is a 3x4, G is a 2x4,
and F is a 2x4.
Press  to give those values to the program. to give those values to the program.
|
Figure 12
|
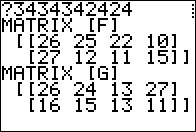
It creates and displays matrix F
and waits for us to press  to move on. Then
it creates and displays matrix G
and waits for us to press to move on. Then
it creates and displays matrix G
and waits for us to press  to move on.
. to move on.
.
|
Figure 13
|
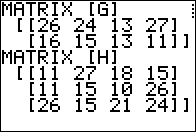
It creates and displays matrix H
and waits for us to press  to move on. to move on.
|
Figure 14
|
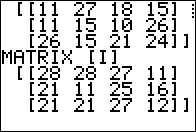
It creates and displays matrix I
and waits for us to press  to move on. to move on.
|
Figure 15
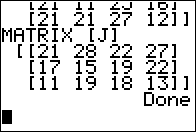
|
It creates and displays matrix J
and the program is done.
|
Figure 16
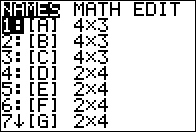
|
We use the   sequence to open the MATRIX menu shown in Figure 16. This provides a
quick confirmation on the size of the matrices now in the calculator.
sequence to open the MATRIX menu shown in Figure 16. This provides a
quick confirmation on the size of the matrices now in the calculator.
|
Figure 17
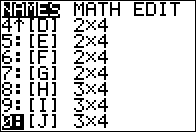
|
To get to Figure 17; we use the  key to move the highlight down to show the remaining matrices.
key to move the highlight down to show the remaining matrices.
We press  to paste the name of the
highlighted matrix, in this case [J], onto the main screen
as is shown in Figure 18. to paste the name of the
highlighted matrix, in this case [J], onto the main screen
as is shown in Figure 18.
|
Figure 18
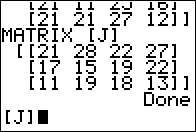
|
To do matrix addition we just need to form the command using the +
sign. We can accomplish this via the  key,
giving the result shown in Figure 19. key,
giving the result shown in Figure 19.
|
Figure 19
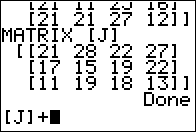
|
In this example we want to add [J] to [H} so we need to get the
name [H]to end our command.
We cannot type that name. Rather, we need to return to the matrix menu,
via   and then use the
and then use the  key to move the highlight to
the desired matrix name. This situation is shown in Figure 20. key to move the highlight to
the desired matrix name. This situation is shown in Figure 20.
|
Figure 20
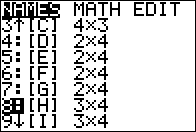
|
Press  to paste [H] onto the home screen,
shown in Figure 21. to paste [H] onto the home screen,
shown in Figure 21.
|
Figure 21
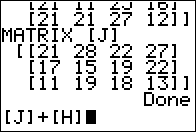
|
With the command completed we just need to press
 to have the calculator perform that command. to have the calculator perform that command.
|
Figure 22
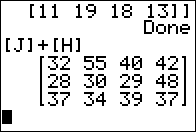
|
The result is shown in Figure 22. Here we see that
It should be clear that the algorith used to add two matrices is
to form a new matrix, of the same dimension,
where the elements of the new matrix
are just the sum of the corresponding elements of the original
two matrices. In this example, the 32 in the
first row, first column of the answer is just the sum of the
21 and 11 that are in the same position
in [J] and [H], respectively.
The requirement for adding two matrices is that they have to have the same
dimensions, i.e., they must have an identical number of rows and an
identical number of columns. Our example worked because the two original matrices
each had 3 rows and 4 columns.
|
Figure 23

|
One important property of addition that we learned when dealing with numeric
values is that the opertion of addition for numbers is
commutative, which means that
x + y = y + x.
Considering that to add two matrices we just add the respective component elements of the
matrices we should expect that the operation of addition for matrices is commutative.
Giving an example does not prove that this is true, but Figure 23 does show that
[H]+[J] gives the same result as we had for [J]+[H].
|
Figure 24

|
Another numeric property of addition is that the operation is associative.
That means that for any numbers, x, y, and z
it is always true that
x + (y + ) = (x + y) + z.
We can give an example of this for matrices. In Figure 24 we find [H]+([I]+[J]).
|
Figure 25

|
Then in Figure 25 we find
([H]+([I])+[J]. The result is the same. Again, this is not a shock
given that when we add matrices we are just adding corresponding elements
from the matrices involved.
This is not a proof. Rather it is an illustration the
addition of matrices is associative.
|
Figure 26
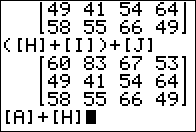
|
What happens on the calculator if we try to add matrices that do not have
the same dimensions? We can try this via
[A]+[H], trying to add a 4x3 and a 3x4 matrices. Figure 26 shows the command.
Press  to ask the calculator to perform the command. to ask the calculator to perform the command.
|
Figure 27
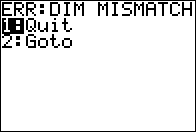
|
The calculator detects the error and reports it
as shown in Figure 27.
We can press Press  to choose to Quit the task.
This returns us to the main screen, shown in Figure 28. to choose to Quit the task.
This returns us to the main screen, shown in Figure 28.
|
Figure 28
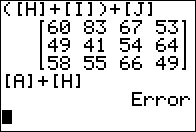
|
Note that the alculator marked the previous command as an Error.
|
Figure 29
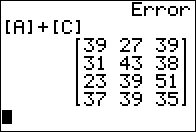
|
We saw that we could not add [A] and [H],
but we can add [A] and [C]. The result is shown in Figure 29.
|

 key.
key.

 key to find and highlight
the GNRNDM program. Then press the
key to find and highlight
the GNRNDM program. Then press the
 key to move to Figure 03.
key to move to Figure 03.

 to have the calculator
run the GNRNDM program
to have the calculator
run the GNRNDM program


 to move forward.
to move forward.

 to give those values to the program.
to give those values to the program.

 to move on.
to move on.

 to move on.
to move on.

 to move on.
to move on.

 to move on. Then
it creates and displays matrix E
and waits for us to press
to move on. Then
it creates and displays matrix E
and waits for us to press  to move on.
to move on.

 to give those values to the program.
to give those values to the program.

 to move on. Then
it creates and displays matrix G
and waits for us to press
to move on. Then
it creates and displays matrix G
and waits for us to press  to move on.
.
to move on.
.

 to move on.
to move on.

 to move on.
to move on.

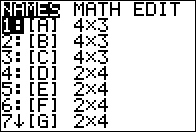

 sequence to open the MATRIX menu shown in Figure 16. This provides a
quick confirmation on the size of the matrices now in the calculator.
sequence to open the MATRIX menu shown in Figure 16. This provides a
quick confirmation on the size of the matrices now in the calculator.
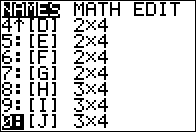
 key to move the highlight down to show the remaining matrices.
key to move the highlight down to show the remaining matrices.
 to paste the name of the
highlighted matrix, in this case [J], onto the main screen
as is shown in Figure 18.
to paste the name of the
highlighted matrix, in this case [J], onto the main screen
as is shown in Figure 18.

 key,
giving the result shown in Figure 19.
key,
giving the result shown in Figure 19.


 and then use the
and then use the  key to move the highlight to
the desired matrix name. This situation is shown in Figure 20.
key to move the highlight to
the desired matrix name. This situation is shown in Figure 20.
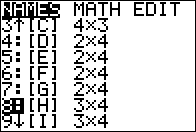
 to paste [H] onto the home screen,
shown in Figure 21.
to paste [H] onto the home screen,
shown in Figure 21.

 to have the calculator perform that command.
to have the calculator perform that command.





 to ask the calculator to perform the command.
to ask the calculator to perform the command.

 to choose to Quit the task.
This returns us to the main screen, shown in Figure 28.
to choose to Quit the task.
This returns us to the main screen, shown in Figure 28.

