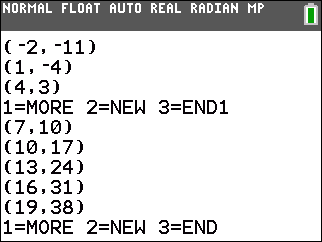
 |  |  | [Note: the images on this page tend to be small. On the computer screen you can point to an image, right click on it, and ask to view the image. Doing so should give you a larger version of the image.] |
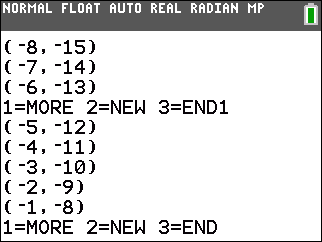
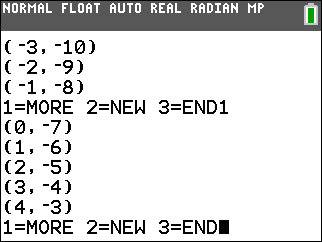
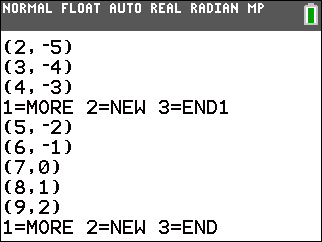
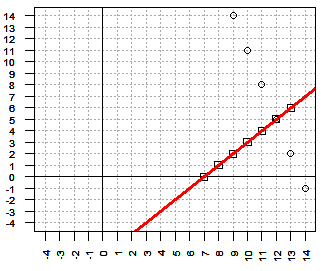
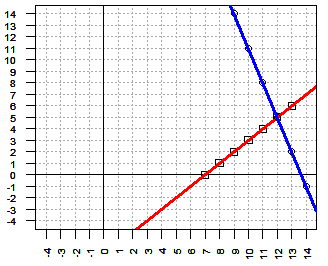
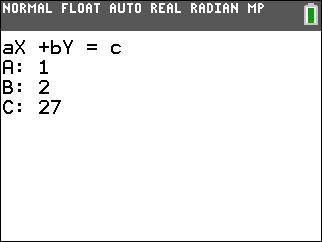
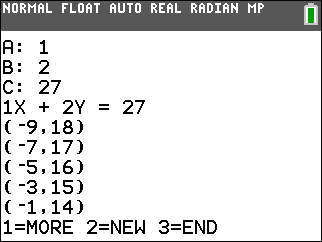
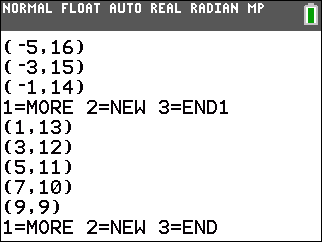
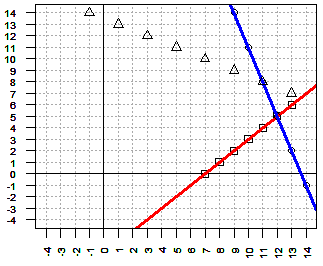
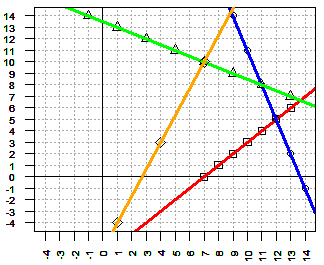
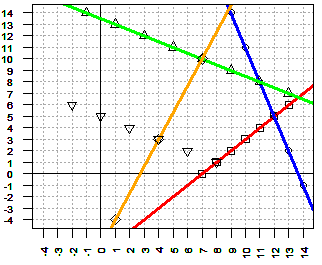
| -1x + y ≥ -7 | 3x + 1y ≤ 41 | x + 2y ≤ 27 |
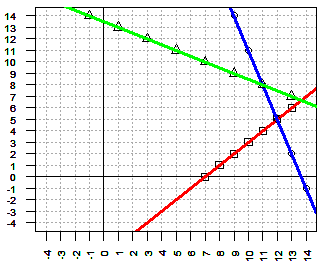
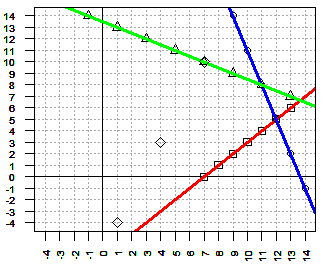
| -7x + 3y ≤ -19 | x + 2y ≥ 10 |
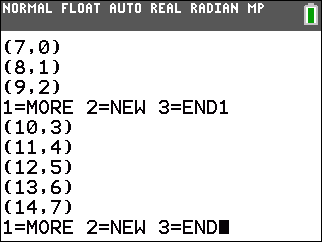
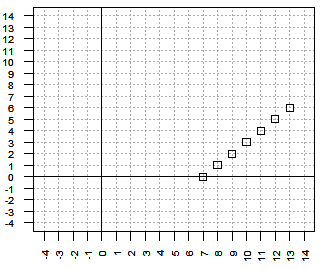
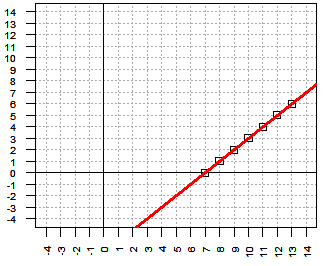
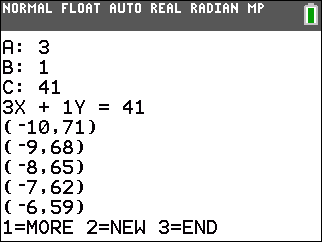
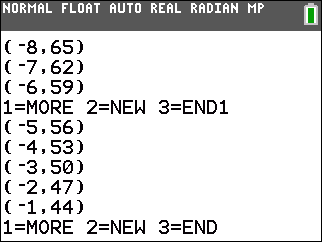
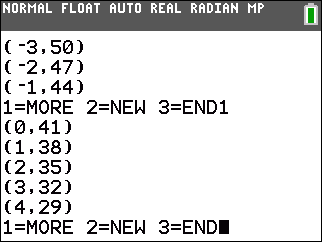
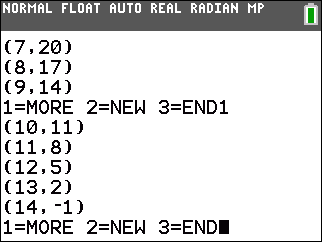
| -1x + y = -7 | 3x + 1y = 41 | x + 2y = 27 |
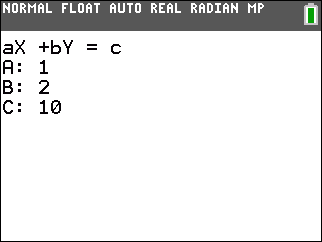
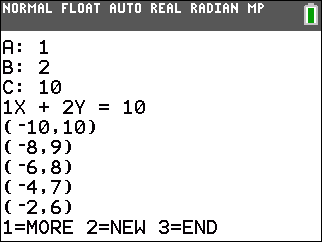
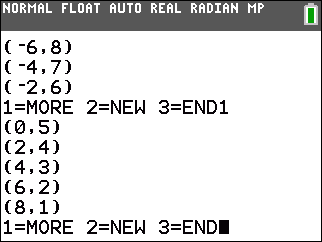
| -7x + 3y = -19 | x + 2y = 10 |
 |  |  | [Note: the images on this page tend to be small. On the computer screen you can point to an image, right click on it, and ask to view the image. Doing so should give you a larger version of the image.] |
 |  |  |  |
 |  |  |
 |  |  |  |
 |  |  |  |
 |  |  |  |
 |  |
 |  |  |
 |  |
 |  |  |
 |  |  |
 |  |
 |  |  |