Now we will repeat the list but with a discussion of how to go about solving such a problem.
|
1. You are given the slope and the y-intercept, find the equation of the line
|
| | Since we know the slope-intercept form of a linear equation
looks like y = mx + b, where m is the slope and b is the second coordinate of the
y-intercept, we have been given everything that we need to just
write the equation. We just plug in the given values. So, if we are given that the slope is 2/3 and the
y-intercept is (0,6) then the equation is y=(2/3)x + 6.
|
|
2. You are given the slope and a point on the line, but not the intercept, find the equation of the line
|
| | Knowing the slope but not the y-intercept means tht we could write a portion of the
desired equation, but not all of it. We start with the slopeintercept form
of the equation, y = mx + b, and we substitute the given value of the
slope for m. So, if we are given that the
slope is (-3/4) and that the line contains the point (8,1), then we know that
we could at least write the equation as y = (-3/4)x + b. The other piece
of information is that the point (8,1) is on the line. But that means that the values x=8 and y=1
must make the equation work. Replacing x and y
in the equation y = (-3/4)x + b with 8 and 1 respectively
we now have the equation
1 = (-3/4)8 + b
but this is an equation in one variable, b and we can solve for that variable:
1 = -6 + b
7 = b
which means that we now know the second coorcinate of the y-intercept and the problem has become identical to the first one;
we can just write the answer
y = (-3/4)x + 7
|
|
3. You are given two points on the line, find the equation of the line
|
| | In this case we are not given the slope and we are not given the y-intercept.
However, if we have two points, we can find the slope of the line between them. The slope between points
(x1,y1)
and (x2,y2) is defined as
| |
y2 - y1 |
| slope = m = |
|
| | x2 - x1
|
This means that we can compute the slope and therefore change this problem into the one we solved above.
The steps are
- look at the coorcdinates of the two points
- figure out the numberator and the denominator of the fraction that is the slope
- if the denominator is zero, then this is a vertical line and the equation
will be of the form 1x+0y=C, where C is the x-coordinate of either point that we are given (the two points
must have the same x-coordinate if the denominator, x2 - x1
is zero). And, in this case, wqe are done.
- IF the denominator is not zero then we can reduce the fraction that is the slope by
dividing the numerator and the denominator by the
greatest common factor of the numerator and the denominator.
- now we have the slope and we can take either of the two given points, substitute the slope for m and the
coordinates of that point for x and y in the equation y = mx + b
and solve for b. After that, we know the slope m and the value of b which
means that we can write the equation using those values.
The process becomes so straight forward that we can write a program to do this. Such a program,
slope.83p
for the TI-83 family, is given below.
 A sample run of the program follows, finding the equation of the line
through the two points (5,9) and (7,-1).
A sample run of the program follows, finding the equation of the line
through the two points (5,9) and (7,-1).
Screen 1
 |
Move to the program listing by pressing the  key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE program.
To leave this screen, press the key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE program.
To leave this screen, press the  key. key.
|
Screen 2
 |
Start the program by pressing the  key. key.
|
Screen 3
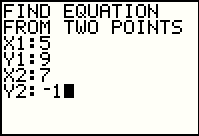 |
The program asks for each of the coordinates of the two points.
Be sure to enter them in the correct order. Here the calculator has been given the points (5,9) and (7,-1).
Press the  key after each coordinate value. key after each coordinate value.
|
Screen 4
 |
The program calculates and displays the SLOPE (in this case -5) and the second
coordinate of the Y-INTERCEPT, in this case 34. Thus, the slope-intercept form of the equation would be
y = -5x + 34
The program then goes into a "pause" mode, indicated by the line of dots in the
upper right corner of the screen. This gives you a chance to read the screen before more information
is displayed Press the  key to continue. key to continue.
|
Screen 5
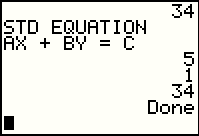 |
The program now displays the calculated values of A, B, and C in the standard form
Ax + By = C. In this case that would be
5x + 1y = 34
|
The program is pretty good, though the output is a bit unpleasant. It is slightly more difficult to obtain nicer looking output on the
TI-83 family of calculators. If your calculator has the program
TOSTR on it then the program SLOPE1,
listed below in three parts,
produces better output.
A comparison of the two programs will show that the SLOPE1 program is merely an extension of
the SLOPE program with the added lines merely making the output nicer. A sample run of the SLOPE1 program
follows:
Screen 1
 |
Move to the program listing by pressing the  key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE1 program.
To leave this screen, press the key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE1 program.
To leave this screen, press the  key. key.
|
Screen 2
 |
Start the program by pressing the  key. key.
|
Screen 3
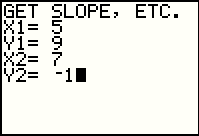 |
The program asks for each of the coordinates of the two points.
Be sure to enter them in the correct order. Here the calculator has been given the points (5,9) and (7,-1).
Press the  key after each coordinate value. key after each coordinate value.
|
Screen 4
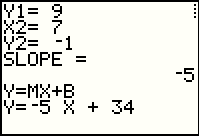 |
The program calculates and displays the SLOPE (in this case -5) and the second
coordinate of the Y-INTERCEPT, in this case 34. In this program the
general slope-intercept form is given, Y=MX+B, and that
is followed by the actual equation:
y = -5x + 34
The program then goes into a "pause" mode, indicated by the line of dots in the
upper right corner of the screen. This gives you a chance to read the screen before more information
is displayed Press the  key to continue. key to continue.
|
Screen 5
 |
The program now displays the standard form
Ax + By = C and follows that with the desired equation
5x + 1y = 34 in standard form.
|
|
|
4. You are told that the line is horizontal and given a point on the line, find the equation of the line
|
| | A horizontal line ahas a slope of 0 so the slope-intercept
equation becomes y = 0x + +b which we can simplify to
y = b. The value of b has to be the same value as the
second coordinate of the given point. [If it were not the smae then the
slope between the y-intercept and the given point could not be 0.]
Therefore, we can use that second coordinate in place of the constant b and just write the equation.
Thus, the equation of the
horizontal line through (5,7) must be y = 7.
|
|
5. You are told that the line is vertical and given a point on the line, find the equation of the line
|
| |
Vertical lines have undefined slope. In this case, the first coordinate
of everypoint on the line is some constant value. If we are given a point on the line then
the first coordinate of that point is the value of x that defines the line.
We can write the equation in standard form as x 0y = C where C
is the first coordinate of the given point. [We make the coefficient of y be 0 so that
the value of the y-coordinate for any point is immaterial to the equation. Also, note
that since the slope is undefined, we cannot write the equation in slope-intercept form.]
Thus, the equation of the
vertical line through (5,7) must be x = 5.
|
|
6. You are told that the line is parallel to a line given in slope-intercept form, and that the
new line contains a point, find the equation of the line
|
| | This is just a wordy version of an earlier problem.
Parallel lines have the same slope.
We are given the slope-intercept form of a line, therefore must be given the desired slope for our new line.
Thus, we know the slope and a point on the line, a problem we already addressed. To find the
equation of a line parallel to y=(-2/3)x + 8 and that contains the point (-6,5) we
really want to find the equation of a line with slope (-2/3) and containing the point (-6,5).
As before, the slope intercept form of the answer can be partially filed out as
y = (-2/3)x + b. We know that (-6,5) must make the equation valid.
Substituting -6 for x and 5 for y we get
5 = (-2/3)(-6) + b which simplifies to
5 = 4 + b and that becomes 1 = b. Finally, we fill out
the slope-intercept form with the the known values and have y = (-2/3)x + 1.
|
|
7. You are told that the line is perpendicular to a line given in slope-intercept form and that
the line contains a point, find the equation of the line
|
| |
With the exception of horizontal and vertical lines, two lines are perpendicula if and only if the
product of their slopes is -1. This means that a line with slope (3/5) is perpendicular to a line
with slope (-5/3). Thus, given a slope-intercept equation for a line we can find the slope of that
line and from that value we compute its negative reciprocal which becomes the slope of our new line. And, again,
we have changed this problem into an earlier one since we now know the slope of the line and
a point on the line. For example, to find the equation of a line that is
perpendicular to the line y = (3/5)x + 7 and contains the
point (-9,-7) we know that we want to find the equation of
a line with slope (-5/3) and containing (-9,-7). The partially completed
slope-intercept form of the answer will be
y = (-5/3)x + b. We know that (-9,-7) must make the equation valid.
Substituting -9 for x and -7 for y we get
-7 = (-5/3)(-9) + b which simplifies to
-7 = 15 + b and that becomes -22 = b. Finally, we fill out
the slope-intercept form with the the known values and have y = (-5/3)x - 22.
|
|
8. You are told that the line is parallel to a line given in standard form and that the new line
contains a point, find the equation of the line
|
| | A short answer to this kind of problem is to change the standard form
of the given equation into slope-intercept form, thus changing the problem into
one we have examined already. That will work! However, if we do this using the standard form we see that:
Ax + By = C
By = (-A)x + C
y = (-A/B)x + (C/B).
In particular, the slope is completely determined by the values of A and B.
Therefore, a new line that is parallel to the given line will have the same slope, which
means that A and B will be the same for the new line. All we have to do is to find C.
The one extra piece of information is that some point is on the new line. But that means that the equation of the new line must work
if we substitute the coordinates of the new point for x and y in the equation. From that we can find
the value of C.
For example, to find the equation of a line that is parallel to
3x + 7y = -12 and that goes through (4,5) we know that the answer will look like
3x + 7y = C, and we know that we can substitute 4 for x
and 5 for y. This gives us 3(4) + 7(5) = C, but that simplifies to
12 + 35 = C which resolves to 47 = C. Therefore, the
desired answer is 3x + 7y = 47.
|
|
9. You are told that the line is perpendicular to a line given in standard form and that the new line
contains a point, find the equation of the line
|
| | Just as in the previous section,
a short answer to this kind of problem is to change the standard form
of the given equation into slope-intercept form, thus changing the problem into
one we have examined already. That will work! However, if we do this using the standard form we see that:
Ax + By = C
By = (-A)x + C
y = (-A/B)x + (C/B).
In particular, the slope is completely determined by the values of A and B.
Therefore, a new line that is perpendicular to the given line will have a slope which is the negative reciprocal of
(-A/B), which
means that A and B will swap places for the new line and we need to change the sign of one of them.
All we have to do is to find C.
The one extra piece of information is that some point is on the new line.
But that means that the equation of the new line must work
if we substitute the coordinates of the new point for x and y in the equation.
From that we can find
the value of C.
For example, to find the equation of a line that is perpendicular to
3x + 7y = -12 and that goes through (4,5) we know that the answer will look like
7x - 3y = C, and we know that we can substitute 4 for x
and 5 for y. This gives us 7(4) - 3(5) = C, but that simplifies to
28 - 15 = C which resolves to 13 = C. Therefore, the
desired answer is 7x - 3y = 13.
|


 key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE program.
To leave this screen, press the
key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE program.
To leave this screen, press the  key.
key.

 key.
key.
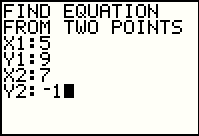
 key after each coordinate value.
key after each coordinate value.

 key to continue.
key to continue.
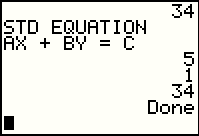


 key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE1 program.
To leave this screen, press the
key.
Then use the arrow keys to move down the list to select (highlight) the SLOPE1 program.
To leave this screen, press the  key.
key.

 key.
key.

 key after each coordinate value.
key after each coordinate value.
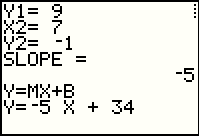
 key to continue.
key to continue.
