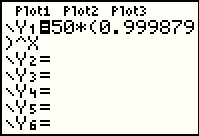

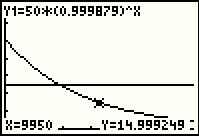
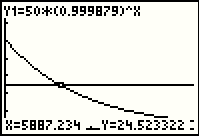
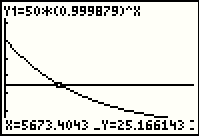

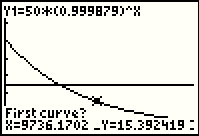
 key to accept that as the other function.
key to accept that as the other function.
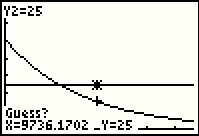
 repeatedly to move the highlight to the left,
in fact going a bit to far to arrive at the next image.
repeatedly to move the highlight to the left,
in fact going a bit to far to arrive at the next image.
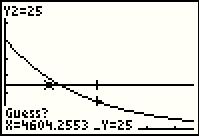
 key to start the search for the
point of intersection.
key to start the search for the
point of intersection.
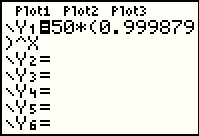
| First we set the function in the Y= screen |

| Then we set the appropriate values for the WINDOW. |

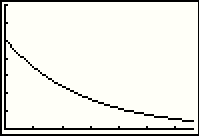
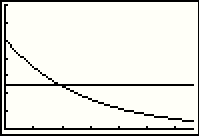
| Now we can GRAPH the function. This looks like the graph on page 69 of the text. |

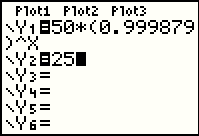
| Here we add the constant function Y2 = 25 to mimic the graph in the book. |

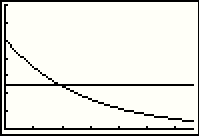
| Returning to the GRAPH, we now see both functions. |
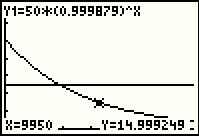
| Pressing the |
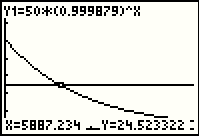
| Using the |
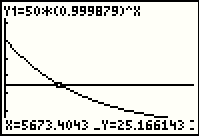
| Moving a step to the left, we have new values and we can certainly, to the nearest 1000 years, be sure that the correct answer is 6000. However, just for the sake of the example, what if we wanted to know a better value for years to get 25 grams. That is, we want to know where the two graphs intersect. |

| Here we returned to the original GRAPH. |

| Pressing the |
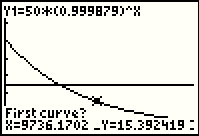
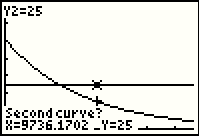
| Now the calculator wants to know which two graphs to examine. This seems a bit strange since there are but two
functions defined, but it would be possible to have three or more functions
defined and then we would need to select the appropriate pair. The calculator is offering the
|

| Now the second function (Y2=25) is identified, again
press the  key to accept that as the other function. key to accept that as the other function.
|
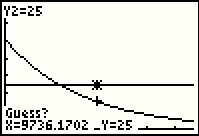
| Here the calculator is asking us to position the highlight at a good guess. We
will use the  repeatedly to move the highlight to the left,
in fact going a bit to far to arrive at the next image. repeatedly to move the highlight to the left,
in fact going a bit to far to arrive at the next image.
|
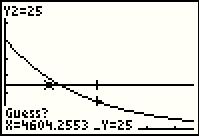
| At this point we can press the  key to start the search for the
point of intersection. key to start the search for the
point of intersection.
|

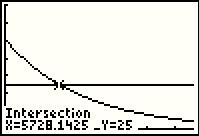
| Here the calculator has solved the question, or at least it has given us a great approximation to the solution with the answer being that after 5728.1425 years we would have 25 grams of carbon 14. |
©Roger M. Palay
Saline, MI 48176
August, 2010