Make sure that the calculator has been turned on (press the
![]() key), and it
might be a good idea to start with a clear screen (press the
key), and it
might be a good idea to start with a clear screen (press the
![]() key).
key).

|
In order to create a list we will need to be able to
use the left brace, {, and the right brace, }. These
characters are not on the keyboard. We press the
|

| We want to start our list with a left brace, {.
Therefore, press the |
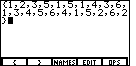
| A LIST is
a sequence of numbers separated by the comma character. Our list is the values in
the data set. Therefore, we enter the values one after the other, just as they were
given, and place a comma between values.
The key sequence is
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 
 .
We conclude the LIST with a right brace, selected from the menu by
pressing the .
We conclude the LIST with a right brace, selected from the menu by
pressing the
 key. This should leave the screen
as in Figure 3. key. This should leave the screen
as in Figure 3.
|
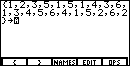
| In Figure 3 we have constructed a LIST.
However, we want to save that LIST.
To do this we need to store the list.
We press the  key to paste the "store" symbol,
key to paste the "store" symbol, |
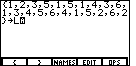
| We store the list to a variable. We get to make up the name for that variable.
In this example we will store the list to a variable called L1.
Variable names need to start with a letter,
and then they can be up to eight characters
long, using letters and digits.
To get the
"L" we press the  key. This will produce
Figure 5. Now, to complete the name we need to
shift out of ALPHABETIC MODE. key. This will produce
Figure 5. Now, to complete the name we need to
shift out of ALPHABETIC MODE.
|
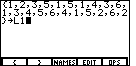
| Press the  key shift out
of ALPHABETIC MODE and then press the key shift out
of ALPHABETIC MODE and then press the
 key to generate the "1",
as in Figure 6. key to generate the "1",
as in Figure 6. |
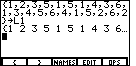
| Through Figure 6 we have constructed a list and formulated
the command to store it in a variable called L1. However, we have not told
the calculator to perform those actions. We do this by pressing the
 key.
The calculator responds by displaying the new list. Note that there are
no commas in this displayed list. Furthermore, the list runs off the screen,
with three dots, ..., following the 6. Those dots indicate that there is
more to the list. We can see more of the list by pressing the key.
The calculator responds by displaying the new list. Note that there are
no commas in this displayed list. Furthermore, the list runs off the screen,
with three dots, ..., following the 6. Those dots indicate that there is
more to the list. We can see more of the list by pressing the
|
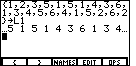
| Figure 8 shows the result of having pressed the
|
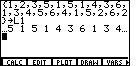
| Now we are rady to perform the statistical computations. We close
the LIST menu of Figure 8 by pressing the
|

| Of the options of the STAT menu, we want
to select the first option, CALC.
To do this we press
Within that submenu, we want to do the OneVar operation, which is
abbreviated to OneVa as the first item in the submenu. We press
|

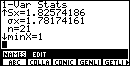
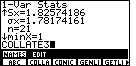
| The full command that we want is |
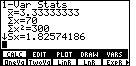
| We formed the entire command in Figure 11. Now we press
The next line, Just to the left of the |
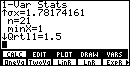
| We press the
Then, the output goes on to report the minimum value found in the list,
|

| We press |

| Before we go any further, let us close the submenu by pressing the
|
Now we will turn our attention to finding the mode of the data. Unlike the finding the mean, the TI-86 does not have a built-in process for finding the mode. We have a program written for the TI-86 that will help in finding this value. That program is called COLLATE3. You can get a copy of the program from another TI-86 that has it, or you can use the TI-Graph Link program to transfer COLLATE3 from a PC that is storing it. The page collate3.htm holds a listing of the program (in case you want to type it into your calculator) and it has a link that will allow you to download the program to a PC (for subsequent transfer via TI-Graph Link).
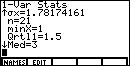
| To get to our program we could type the name of
the program, or we can use the menu system to find the
name and paste it onto the screen. To use the latter approach we press
|
| Next we press
|
| Pressing
|

| To actually start the program we need to press the
|

| We can respond to the prompt of Figure 19
by pressing |

| Having formed the response in Figure 20, we press
|
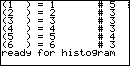
| We press the
We can examine the second and third columns to find the mode value of the data set. The mode will be the value in the second column that corresponds to the largest value in the third column. In Figure 22, 5 is the largest value in the third column. Therefore, the mode of the data set is 1, the value of the second column that corresponds to the 5 in the third column. We can also use the output of Figure 22 to find the median. The median was a result produced by OneVar above. This is just another way to arrive at the same result. Remember that the median is the middle value in the sorted data values. We remember, from Figure 13, that there were 21 values in our data set. That means that if we sort the values, then we want the 11th value (it will have 10 values that are less than or equal to it and 10 that are greater than or equal to it). From Figure 22 we see that there are 5 1's, 3 2's, and 3 3's. Therefore, the 11th value is a 3, which makes the median of the data set be 3. [We will see yet another way to find the median in the second example.] |
| In the example that we are using there are only six different values. Therefore,
Figure 22 gave the complete list of values in the data set. We are ready to move
on from that report. We press
|
Figures 16 through 23 demonstrated the use of the COLLATE3 program. We will return that program in the second example data set below for a more complete illustration of the output. However, Figure 21 had some information that was not explained at that time. In particular, Figure 21 included a reference to two new lists, OCL and ONL. We will take a moment to examine these lists, which are produced by the COLLATE3 program.
| To move to Figure 24 we need to close the
histogram. We do this by pressing the |
| To view the new lists we will open the LIST menu by pressing
|
| Then we will select the
NAMES option by pressing the
|

| Pressing the
|
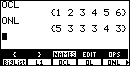
| Let us clear the screen by pressing the
The submenu in Figure 28 has a small arrow at its extreme right. This means that there are more list name to display. |
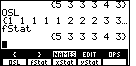
| We press
OSL is a copy of the original list, L1, except that the values in OSL have been sorted into ascending order. fStat appears to be a copy of the list that we had before, ONL, the list holding the frequency of the different values. |
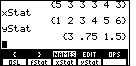
| The press
xStat is a copy of the earlier list, OCL, the list holding the individual distinct values in our list. yStat has values that we have not seen before. In fact, yStat has values left over from some earlier use of this particular calculator. |
The last two screens illustrated the fact that COLLATE3 generates lists OCL and ONL to hold the separate values of our original list and the frequency of those values. Furthermore, COLLATE3 generates a sorted copy of the original list in OSL. And, it appears that OCL has been copied into xStat and the ONL has been copied into yStat. If you examine the program listing for the TI-86 version of COLLATE3, you will find, on the fifth and fourth last lines of the program, statements to perform this copying. Once COLLATE3 has been allowed to complete normally, those copies will have been made.
The first 30 Figures demonstrate statistical processing for a 21-element data set. It is nice to see the TI-86 do all of the computations, but the process seems to take many steps just to process those 21 values. The real power of the TI-86 can be seen if we look at processing a much larger set of data. For example, consider the following table of numbers taken from a sample test on this material.
| -113 | -133 | -132 | -91 | -123 | -121 | -93 | -103 | -104 | -102 | -106 | -126 | -136 | -90 | -120 |
| -105 | -140 | -125 | -127 | -110 | -109 | -109 | -128 | -88 | -114 | -133 | -143 | -120 | -97 | -108 |
| -102 | -107 | -96 | -108 | -91 | -115 | -122 | -122 | -82 | -111 | -130 | -116 | -97 | -122 | -107 |
| -85 | -135 | -116 | -116 | -94 | -91 | -142 | -119 | -119 | -121 | -115 | -117 | -120 | -136 |
We could process this data using exactly the same steps that we used before. The first step will be to get this list into the calculator. Even that seems to be a formidable task. However, in this case, you can generate this same list on your calculator as as L1 via the gnrnd6 program on the TI-86 with SEED 1= 54365448139 and SEED 2= 5391885598 and CHECKSUM=232. We will demonstrate using the program to do this.
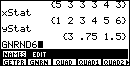
| We move from Figure 30 to Figure 31
by pressing |

| Pressing the |

| We supply the seed value by pressing the keys
to generate 54365448139 and then we press the
|

| We enter the
digits for 5391885598 and press
|

| We signal that we are done with the input by pressing the
Once the list has been created, the TI-86 will display the list and it will pause so that we may examine the newly generated list. Note that the line of small dots running up the top right side of the screen indicates that we are in a paused condition. The three dots at the right end of the displayed list indicate that we can use the cursor keys to shift the display so that we can review more of the list. |

| We generate Figure 36 by pressing
|

| Remembering that we are not done with the program, it is in a paused
condition, we press
|
| Now that the COLLATE3 program
has created the list of values in L1, we need to perform
a one variable statistical analysis on those numbers. To do this
we can return to the STAT menu by pressing
|
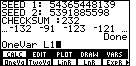
| Next, we append L1 to our command by pressing
|
| We tell the calculator to perform our command by pressing the
|

| We can close the submenu via the
|

| Pressing That still leaves us with finding the mode and the frequency distribution table. |

| To find these remaining values we will open the
PROGRAM menu by pressing |

| We start the COLALTE3 program by pressing
|

| Press
|
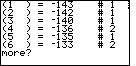
| We leave Figure 45 and start the display of the table by pressing
|
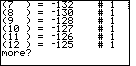
| Press |

| We press |
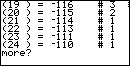
| To move to Figure 49 we press |
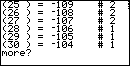
| Another |
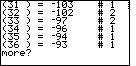
| Another |
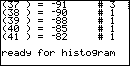
| And, with one more |

| At the end of Figure 52 the calculator
suggested that it was ready to produce a histogram.
We press |

| In this case we attempt to suggest to the TI-86 that
it should use a grouping factor of 2. We do this
by pressing the |
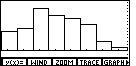
| We press |

| As noted in the earlier example,
the histogram is on the graphics screen. We can leave
that screen and return to the main screen
by pressing |
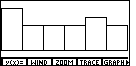
Between the built-in statistical features of the TI-86 and the COLLATE3 program we have been able to find the mean, median, and mode of the data values in our list. In addition, we have found the range, the quartile points, and the population standard deviation. The COLLATE3 program also gives us a frequency distribution table, and a histogram.
The collate3 program has some additional by-products. The output for the frequency distribution table is taken from two lists that COLLATE3 creates. The list OCL holds each of the different values found in the original list. The list ONL holds the frequency of occurrence for each of the corresponding values in OCL.
We will recall that the form of the OneVar command demonstrated above required one list, but OneVar has other forms as well. The syntax for the OneVar command allows us to follow the command with a single list of values. That is what we have demonstrated above. Alternatively, the OneVar command allows us to follow the command by two lists, the first holding the different values, and the second list holding the frequency for each corresponding value. That is, the results that we saw in Figure 40 through 42 were the result of the OneVar command in Figure 39. After we have run the COLLATE3 program (that is, after we have generated OCL and ONL) we could use this alternative syntax to issue the command "OneVar OCL,ONL". This would produce exactly the same results that we saw in Figures 40 through 42.
Also, to do its work, COLLATE3 always produces a list called OSL, a copy of the original list but sorted into ascending order. We could have used that list to find values such as the median or the quartile points. There were 59 items in the original list. Therefore, in OSL, which holds the same 59 items but sorted, the 30th item will be the median value. Let us examine this.

| We will start by opening the LIST
menu via the |
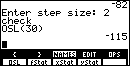
| Press
|
| In the same way the first and third quartile points will be in
positions 15 and 45 of the sorted list. We can have the calculator
display those values via the keys
|
Remember the frequency distribution table output generated by COLLATE3 (see Figures 46 through 52). The explanation of COLLATE3 given above tells us that the values for those displays came from the two lists OCL and ONL. In addition, when we first looked at the lists generated by COLLATE3, we found that OCL is copied to xStat, and ONL is copied to fStat. We will use the Stat Editor of the TI-86 to take a second look at those values.

| We left Figure 59 with the STAT menu and its NAMES submenu open.
We can select the EDIT option from the STAT menu
by pressing the
|
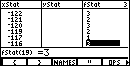
| We can see even more of the values by pressing
|
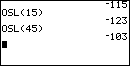
| We return to the main screen by pressing
|
Let us return to the problem of the histogram on the TI-86.
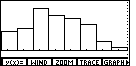
| We press |

| We press
|
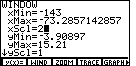
| We can press |

| Now, with the new xScl value set, we press
As we examine Figure 66 we do note that the bars are all fairly short. If we look back at Figure 65, we note that the yMax value is 15.21. It is that value that is determining the height of the largest possible bar. We could easily lower that value. |
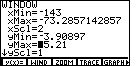
| We return to the WIND menu via the
|
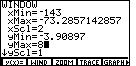
| We can change the yScl value to 8 by pressing
|
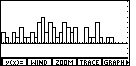
| And we return to the graph screen by pressing
Before we leave this screen, remember that the horizontal axis is representing all negative numbers for this particular data set. That does explain the dots along the right side of the screen. They are the "tic" marks that inidcate the vertical scale on the screen. The yScl line in Figure 68 has the value 1. Thus, in Figure 69, each of those "tic" marks indicates a step of 1. The highest bar on the screen is only 5 marks high. Thus, that bar represents a frequency of 5. |
©Roger M. Palay
Saline, MI 48176
January, 2000