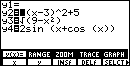
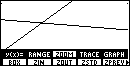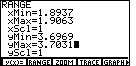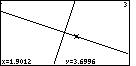Now that we can see the graphs in Figure 18,
it turns out that I do not want graphs that are so close together.
We will change the problem requirements so that the
second function becomes g(x)=3x+11.
As we look at Figure 26, we might be concerned by the fact that the
graph of the last function does not appear to be perpendicular to the
graphs of the first two functions. Each of the first two functions has slope=3.
The last function has slope=-1/3. We may know that lines with slopes that multiply to be -1 are
supposed to be perpendicular, that is, they should meet in a 90° angle.
However, looking at Figure 26, those lines do not appear to be perpendicular.
The problem is in the RANGE settings. The screen on the calculator has
many more points going across the screen than it does going up and down the screen.
Therefore, with a ZSTD setting, where
the x-values go from -10 to 10 and the y-values
go from -10 to 10, the screen is essentially stretched left and right to use the extra
horizontal points on the screen.
The screen is made up of lots of dots, called pixels (for picture elements),
arranged in rows and columns. There are only so many
vertical pixels and there are more horizontal pixels.
The Y-values are spread from -10 to 10 across the vertical pixels.
The X-values are spread from -10 to 10 across the horizontal pixels.
Because there are more horizontal pixels, the horizontal dot-to-dot
change in value is different from the vertical dot-to-dot change in value.
The result of this is that lines that should be perpendicular
do not appear to be perpendicular. Also, lines with a slope just slightly more than 1 will
appear as lines sloping at less than 45° from the horizontal. It would be nice if we had some
way to correct for this "stretching", and we do. The calculator has a ZOOM menu option that adjusts
the RANGE settings so that it compensates for the extra width in the screen.
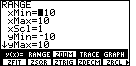
Figure 28
| For Figure 28 we re-open the ZOOM menu by pressing the
 key. The ZOOM option that we want, ZSQR, is not here.
Therefore, we need to look at more of the menu options. key. The ZOOM option that we want, ZSQR, is not here.
Therefore, we need to look at more of the menu options.
|
Figure 29
| We press the  key to
view more of the ZOOM options. The ZSQR option appears in the second
position. We press the key to
view more of the ZOOM options. The ZSQR option appears in the second
position. We press the  key to select the ZSQR
option. The result will be Figure 30. key to select the ZSQR
option. The result will be Figure 30. |
Figure 30
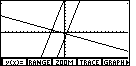
| Here we note that the
third graph does seem to be perpendicular to the other two graphs. Furthermore,
the slope of the first two graphs corresponds a bit better to our expectation for
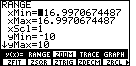
a slope of 3. Let us see what the ZSQR option did to the settings
in the RANGE screen. |
Figure 31

| To get to Figure 31, we press the  key.
Note that the
yMin and yMax values remain as before in Figure 29.
However, the xMin and xMax values
have been changed so that we have a wider Domain. The new values mean that the
dot-to-dot change in values on the x-axis corresponds
to the dot-to-dot change in values on the y-axis.
Therefore, with these settings, graphs will look more the way that we expect them to appear. key.
Note that the
yMin and yMax values remain as before in Figure 29.
However, the xMin and xMax values
have been changed so that we have a wider Domain. The new values mean that the
dot-to-dot change in values on the x-axis corresponds
to the dot-to-dot change in values on the y-axis.
Therefore, with these settings, graphs will look more the way that we expect them to appear.
|
Figure 32
| The previous Figures demonstrated the ZSTD and
the ZSQR options. Now we will look at another option, the ZDECM option.
We open the ZOOM menu via the  key
and then use the key
and then use the  key to display the second
set of options. The ZDECM option is in position 4.
Pressing key to display the second
set of options. The ZDECM option is in position 4.
Pressing  selects and performs that option,
resulting in Figure 33. selects and performs that option,
resulting in Figure 33.
|
Figure 33

| The result of using the ZDECM option is the graph reproduced in Figure 33.
The lines still look perpendicular, but the extent of the graph seems to have been cut down.
Judging by the tick-marks, the x-values run from somewhere less than -6 to somewhere
over 6, and the y-values go from just less than -3 to slightly more than 3. |
Figure 34
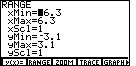
| If we press the  key we return to the RANGE
screen and we can see what ZDECM has really done.
Figure 34 shows us the new values with
the blinking cursor covering the negative sign.
The 6.3 and 3.1 values are just about what we guessed from looking at
Figure 33. key we return to the RANGE
screen and we can see what ZDECM has really done.
Figure 34 shows us the new values with
the blinking cursor covering the negative sign.
The 6.3 and 3.1 values are just about what we guessed from looking at
Figure 33.
It just so happens that there are 63 vertical pixels and 127 horizontal pixels on the
TI-83 screen. By choosing the values shown in Figure 34, the calculator is
making sure that moving one pixel left, right, up, or down, corresponds to a change
of exactly 0.1. Therefore, we will have pixels at points such as (2.0,3.0) and (-3.4,-1.2).
That is why this setting is called ZDECM.
|
Figure 35

| The ZOOM options that we have demonstrated so far,
ZSTD, ZSQR, and ZDECM, have taken immediate effect on
the graph. Now we will look at BOX, an option that requires us to
press a few more buttons. We return to the ZOOM screen
by pressing the  key. key.
The idea of a BOX zoom is that we will draw a box around a portion of
the graph. Then we will have the calculator change the RANGE settings so that
a new GRAPH screen will be that entire box. Let us see how this works.
To select BOX we merely press the  key to select
this option. key to select
this option.
|
Figure 36

| Figure 36 is the result of starting the BOX process. It looks
remarkably the same as Figure 33. However, one point, one dot, one pixel, has
changed. The pixel at the origin, circled in red in Figure 36, is now white.
It is marking a possible location for a corner of the box that we will draw. The
coordinates of that pixel are given at the bottom of the screen, namely x=0 and y=0. |
Figure 37
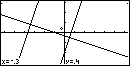
| I want to draw a box around the intersection of the first and third graphs.
To do this I will move the pointer to (-0.3,0.4) by using the
 and and  keys. I have done that
in Figure 37 until I have the pointer at (-0.3,0.4) as noted by the coordinates at the
bottom of the screen. This point will be the upper left corner of the box that I will draw. keys. I have done that
in Figure 37 until I have the pointer at (-0.3,0.4) as noted by the coordinates at the
bottom of the screen. This point will be the upper left corner of the box that I will draw.
|
Figure 38
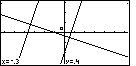
| To signal that this is the location for one corner
we press the  key. The calcualtor responds by
placing a small square at the corner point selected. key. The calcualtor responds by
placing a small square at the corner point selected. |
Figure 39
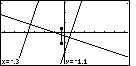
| Now we use the  key to move the pointer
down to the point (-0.3,-1.1). As we do this, the calculator extends the side of the
box from the corner spot that we selected. key to move the pointer
down to the point (-0.3,-1.1). As we do this, the calculator extends the side of the
box from the corner spot that we selected. |
Figure 40
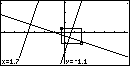
| We use the  key to move the cursor to the right
until we are at the point (1.7,-1.1), causing the calculator to draw the box from the
specified corner to the pointer. In Figure 40 we can see that box. key to move the cursor to the right
until we are at the point (1.7,-1.1), causing the calculator to draw the box from the
specified corner to the pointer. In Figure 40 we can see that box.
This is the box that we want to expand to the full screen size. To accept this box we press the
 key. That will reset the RANGE settings and it will
re-display the graphs in the new GRAPH screen shown in Figure 41. key. That will reset the RANGE settings and it will
re-display the graphs in the new GRAPH screen shown in Figure 41. |
Figure 41

| Figure 41 shows the new display. It is focused onto the box that we drew in Figure 40.
|
Figure 42
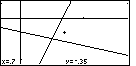
| Figure 42 represents the result of
pressing the  key to start drawing another box.
Notice that the initial point identified in Figure 42 for a corner of a box is
right in the middle of the screen, and, in fact, in the middle of the box that
we had drawn in Figure 40. key to start drawing another box.
Notice that the initial point identified in Figure 42 for a corner of a box is
right in the middle of the screen, and, in fact, in the middle of the box that
we had drawn in Figure 40. |
Figure 43
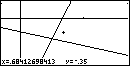
| We will use the cursor keys to re-position the cursor to the point
shown in Figure 43. Notice that we have lost the nice even decimal values
that we had before. This is due to the fact that the box we drew in
Figure 40 did not have the 63 by 127 height to width ratio that we had
established earlier. As a result, the lines no longer look to be
perpendicular.
We press the  key to fix the point in Figure 43 as the
upper right corner of the box we are going to draw. key to fix the point in Figure 43 as the
upper right corner of the box we are going to draw. |
Figure 44
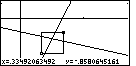
| In Figure 44 we have used the cursor keys to outline
a box that we will expand to the entre screen. |
Figure 45
| We press the  key to complete the
BOX option. The calculator responds by drawing the screen seen in
Figure 45. key to complete the
BOX option. The calculator responds by drawing the screen seen in
Figure 45. |
Figure 46

| We can look at the RANGE setting by pressing the
  keys. The result appears in Figure 46.
Note that the blinking cursor is covering the decimal point in the xMin value. keys. The result appears in Figure 46.
Note that the blinking cursor is covering the decimal point in the xMin value. |
Figure 47

| Now we return to the GRAPH screen by pressing the
 key. Then we will square off the screen by using the
ZSQR option in the ZOOM menu. Finally, we can first hide the double menu via the key. Then we will square off the screen by using the
ZSQR option in the ZOOM menu. Finally, we can first hide the double menu via the
 key, and then recall the single menu
by pressing the key, and then recall the single menu
by pressing the  key. That should leave the
screen as it is seen in Figure 47. key. That should leave the
screen as it is seen in Figure 47.
|
Figure 48

| In Figure 48 we have pressed
the  key one time. A new marker, a large + sign appears.
So do the coordinates of that marker. We can use that marker to move
around the screen, checking the values of the points on the screen. key one time. A new marker, a large + sign appears.
So do the coordinates of that marker. We can use that marker to move
around the screen, checking the values of the points on the screen. |
Figure 49

| In Figure 49 we have moved the marker closer to the point of
intersection of the two lines. |
Figure 50

| In Figure 50 we have moved the + as much onto the intersection of the two lines as
we can. It is partially hidden by the lines. The coordinates suggest that we are quite close to the
point (0.5,-0.5).
We might notice that (0.5,-0.5) is a solution to y=3x-2 and to y=(-x-1)/3. In short,
it is the point of intersection.
For the given xMin, xMax, yMin,
and yMax, the point (0.5,-0.5) is not one of the pixels
on the screen. In a sense it is between pixels. That is why we can get close, but we can not
hit it exactly on the screen in Figure 50. If we were to properly adjust the settings on
the RANGE screen we could get this to be such a point. (xMin=0.437, xMax=0.563,
yMin=-0.531, yMax=-0.469 would work.)
|
Figure 51

| We will return to the ZOOM menu to try out another option. Press
 , as in Figure 51.
The ZOUT option allows us to determine a new center for the graph and then to
increase the horizontal and vertical span around that center point.
Press the , as in Figure 51.
The ZOUT option allows us to determine a new center for the graph and then to
increase the horizontal and vertical span around that center point.
Press the  key to start the ZOUT option. key to start the ZOUT option. |
Figure 52
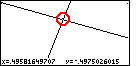
| The red circle drawn in Figure 52 is meant to help identify the blinking
pointer that is at the last place we had the + pointer.
We will leave that point where it is and press the  key
to finish the ZOUT option. key
to finish the ZOUT option.
|
Figure 53
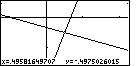
| The ZOUT option has been performed to transform Figure 52 into Figure 53.
The point has not moved, but the graph covers a larger area, as is evidenced by the appearance
of the axes. Also, as expected, our point is now in the center of the screen. And, we are
still in ZOUT mode. We can perform the option again merely by
pressing the  key, which we do to move to Figure 54. key, which we do to move to Figure 54. |
Figure 54
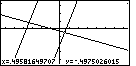
| Here we have moved out further. We can even see the second
function over on the left side. |
Figure 55

| Again, we return to the ZOOM menu, first by pressing the via the  key.
This time we will investigate the ZIN option.
We press key.
This time we will investigate the ZIN option.
We press
 to move to Figure 56. to move to Figure 56. |
Figure 56
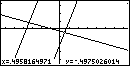
| Again, as in Figure 52, there is a marker at the intersection of the
first and third functions.
It is difficult to see the marker because the lines cover it. However, we can notice the
white spot in the intersection. In addition, we are familiar enough with
the graph to use the coordinates to locate the marker. |
Figure 57
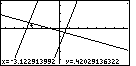
| We use the cursor keys,  and and
 , to move the marker closer to the
intersection of the second and third functions.
Figure 57 shows that we have moved the marker. This will be the
center of a new screen where we focus in on this region.
We press the , to move the marker closer to the
intersection of the second and third functions.
Figure 57 shows that we have moved the marker. This will be the
center of a new screen where we focus in on this region.
We press the  key to
complete the ZIN option. key to
complete the ZIN option. |
Figure 58
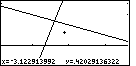
| In Figure 58 we see the result of the ZIN option.
The center is where we had set the marker in Figure 57. We now have a
close-up view of this region. And, we are still in ZIN mode, as
noted by the marker. |
Figure 59
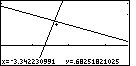
| We will move even closer to the point of intersection, using the cursor
keys.
Figure 59 shows this new location.
Press  to perform another ZIN option. to perform another ZIN option. |
Figure 60
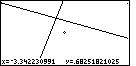
| In Figure 60 we are so close to the point of intersection that we
have lost the axis from the screen. Note that we are
still in ZIN mode. |
Figure 61
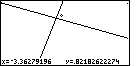
| Repeating the process one more time, we will move the marker so that it is
above and to the right of the point of intersection. This is shown in Figure 61.
Again, press the  key to finish the ZIN option. key to finish the ZIN option. |
Figure 62
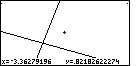
| In Figure 62 we have closed in even more than before, but it is
hard to tell from the screen. After all, we are looking at two straight
lines and at their point of intersection. Once we are so close that we
can not see other lines or the axes, the picture just does not change.
We should notice the change if we moved the marker.
Each time we ZIN, we decrease the change in the coordinates
whenever we move the marker one pixel. |
Figure 63

| We can leave the ZIN mode by pressing the
 key. In Figure 63 we can see the two levels of the menu.
We want to look at the values on the RANGE screen. Therefore, we press key. In Figure 63 we can see the two levels of the menu.
We want to look at the values on the RANGE screen. Therefore, we press
  to move to Figure 64. to move to Figure 64.
|
Figure 64

| Looking at Figure 64, we can see that the entire width of the
graph in Figure 63 represented x-values from about -3.447073704561
to -3.25484687439, while the entire screen height represented y-values
from about .758318158221 to .885334287253. |
Figure 65
| There is more that we want to demonstrate here. Let us return to the
standard view of the GRAPH. To do this we move to the ZOOM menu
via the  key, then select the
ZSTD option by pressing the key, then select the
ZSTD option by pressing the  key,
and then closing the bottom menu via the key,
and then closing the bottom menu via the  key.
The result is shown in Figure 65. key.
The result is shown in Figure 65. |
Figure 66

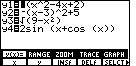
| The next change that we will make will be to modify the third equation
from y3=(-x-1)/3 to y3=(-x+13)/3.
To do this, first move to the y(x)= screen by
pressing the  key.
Then, we use the cursor keys to move the blinking cursor
down to the third line and then across to the subtraction sign,
as shown in Figure 66. key.
Then, we use the cursor keys to move the blinking cursor
down to the third line and then across to the subtraction sign,
as shown in Figure 66.
|
Figure 67

| In Figure 66 we positioned the cursor on top of the subtraction sign.
Now we replace that subtraction with a plus sign by
pressing the  key. Then we move to the right
two places by using the key. Then we move to the right
two places by using the  key twice.
This leaves us with the blinking cursor on top of the right parenthesis, as is shown in Figure
67. key twice.
This leaves us with the blinking cursor on top of the right parenthesis, as is shown in Figure
67. |
Figure 68
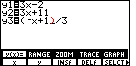
| We want to insert a character here. We move the calculator into INSERT mode
by pressing   .
The blinking block cursor changes to a blinking underline cursor
to indicate that we are in INSERT mode. Figure 68 has been augmented with
a red parenthesis to remind us that the parenthesis character is still there. .
The blinking block cursor changes to a blinking underline cursor
to indicate that we are in INSERT mode. Figure 68 has been augmented with
a red parenthesis to remind us that the parenthesis character is still there. |
Figure 69
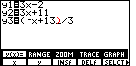
| The character that we want to insert is the number 3, so we
press the  key. We have done this in Figure 69. Since we are in
INSERT mode, the 3 is inserted in the text. The blinking underline
cursor moves to the right, along with the rest of the line. Again,
the figure has been augmented with the red parenthesis. key. We have done this in Figure 69. Since we are in
INSERT mode, the 3 is inserted in the text. The blinking underline
cursor moves to the right, along with the rest of the line. Again,
the figure has been augmented with the red parenthesis.
|
Figure 70
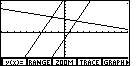
| We exit INSERT mode and return to the GRAPH screen
by pressing the   keys.
The new plot shows the change in the third equation. keys.
The new plot shows the change in the third equation.
|
Figure 71
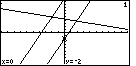
| We have looked at four of the
five menu items in the main menu shown at the
bottom of the screen. Let us check out the remaining menu item.
If we press the  key, the calculator moves
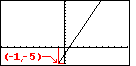
into TRACE mode, shown in Figure 71. The display has been changed by placing the number 1
at the top right corner of the screen.
In addition, a blinking marker is placed on the first equation, in this case at the point (0,-2).
And the coordinates of the location of the blinking marker have been displayed
at the bottom of the screen. key, the calculator moves
into TRACE mode, shown in Figure 71. The display has been changed by placing the number 1
at the top right corner of the screen.
In addition, a blinking marker is placed on the first equation, in this case at the point (0,-2).
And the coordinates of the location of the blinking marker have been displayed
at the bottom of the screen.
In TRACE mode, we use the left and right cursor keys to
move the blinking marker along the equation identified by the number at the top right of the screen.
We use the up and down cursor keys to make the blinking marker jump from one
equation to the next.
|
Figure 72
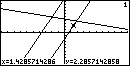
| For Figure 72 we have used just the  key
to move the blinking cursor along the first equation.
Note the changing coordinates as you do this.
We stop, in Figure 72, when x=1.4285714286. key
to move the blinking cursor along the first equation.
Note the changing coordinates as you do this.
We stop, in Figure 72, when x=1.4285714286. |
Figure 73
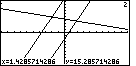
| To move from Figure 72 to Figure 73 press
the  key. This moves the trace from the first
equation, y1=3x-2, to the second equation, y2=3x+11. Notice that the number 2 is
now displayed at the top right of the screen.
But, where is the blinking cursor? If we look at
the coordinates at the bottom of the screen, we see that the x-value has
not changed from what it was in Figure 73. However, the corresponding y-value
for the second equation is y=15.285714286, a point that is off of the screen.
Therefore, we are tracing the second equation, but our marker is off the screen at this point. key. This moves the trace from the first
equation, y1=3x-2, to the second equation, y2=3x+11. Notice that the number 2 is
now displayed at the top right of the screen.
But, where is the blinking cursor? If we look at
the coordinates at the bottom of the screen, we see that the x-value has
not changed from what it was in Figure 73. However, the corresponding y-value
for the second equation is y=15.285714286, a point that is off of the screen.
Therefore, we are tracing the second equation, but our marker is off the screen at this point.
|
Figure 74
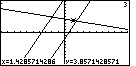
| We can press the  key to
jump the trace to the third equation. The x-value has not changed, but the corresponding y-value is
now on the screen. Therefore, we can see the blinking marker sitting on the
third line. key to
jump the trace to the third equation. The x-value has not changed, but the corresponding y-value is
now on the screen. Therefore, we can see the blinking marker sitting on the
third line.
|
Figure 75
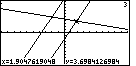
| We will use the  key to move that
blinking marker to the intersection of the
two lines. We can see, in Figure 75, that we are close to the intersection,
that we are tracing the third equation, y3=(-x+13)/3,
that the x-value is 1.90447619048 and the y-value is
3.6984126984. key to move that
blinking marker to the intersection of the
two lines. We can see, in Figure 75, that we are close to the intersection,
that we are tracing the third equation, y3=(-x+13)/3,
that the x-value is 1.90447619048 and the y-value is
3.6984126984. |
Figure 76
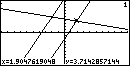
| For Figure 76 we have pressed the  key
so that we are again tracing the y1=3x-2 equation.
The x-value remains unchanged from Figure 75.
However, there is a new y-value, namely, 3.3.7142857144. The two lines are not at the
same y-value for the given x-value. In other words, we are not really at
the point of intersection. Let us zoom in on the picture. key
so that we are again tracing the y1=3x-2 equation.
The x-value remains unchanged from Figure 75.
However, there is a new y-value, namely, 3.3.7142857144. The two lines are not at the
same y-value for the given x-value. In other words, we are not really at
the point of intersection. Let us zoom in on the picture.
|
Figure 77
| For Figure 77 we have shifted to the ZOOM
menu by pressing the  key
to get out of TRACE mode, and then key
to get out of TRACE mode, and then  to open the ZOOM menu.
To leave Figure 77 and
move to Figure 78 we press the to open the ZOOM menu.
To leave Figure 77 and
move to Figure 78 we press the  key to start
the ZIN option. key to start
the ZIN option. |
Figure 78
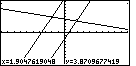
| In Figure 78 we are in the middle of the ZIN option.
Although it is hard to recognize
on the printed screen (because it is not blinking here) the marker is
right where we left it. It does show as a single pixel white spot near the
point of intersection.
|
Figure 79
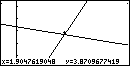
| We move from Figure 78 to Figure 79 by pressing the
 key to perform the ZIN option.
Notice that we can see that the marker is slightly separated from
the lines. key to perform the ZIN option.
Notice that we can see that the marker is slightly separated from
the lines.
|
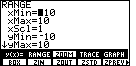
Figure 80
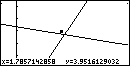
| For Figure 80 we have returned to the
ZOOM menu and selected the BOX option. Then we have located the corner
of the box and we have pressed the
 key to fix that location. key to fix that location.
|
Figure 81

| This picture shows the marker as moved to the opposite corner of the
box. |
Figure 82
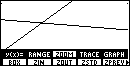
| Having drawn the box in the previous screens, we press the
 key to complete the BOX option.
The result is shown in Figure 82. key to complete the BOX option.
The result is shown in Figure 82.
|
Figure 83

| At this point we can press the  key
three times. This will make the + marker appear and move up from the
center of the screen. key
three times. This will make the + marker appear and move up from the
center of the screen. |
Figure 84

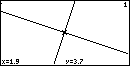
| In Figure 84 we have moved the + marker so that is approximately on top
of the intersection of the two lines. Judging from the coordinates at the
bottom of the screen, the lines cross at or near (1.9,3.7). Let us
manufacture a screen that uses decimal values and that includes this point. |
Figure 85
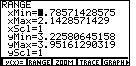
| We can return to the RANGE screen by pressing
  .
Figure 85 gives the current values of the RANGE settings.
To get decimal values we want to have 127 points going across and 63 points
going up and down. .
Figure 85 gives the current values of the RANGE settings.
To get decimal values we want to have 127 points going across and 63 points
going up and down. |
Figure 86
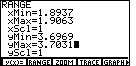
| If we want the screen to have (1.9,3.7) as the center, then we
can set the xMin to 1.9-0.0063, xMax to 1.9+0.0063,
yMin to 3.7-0.0031 and yMax to 3.7+0.0031.
We can do the arthmetic in our heads and enter the correct values, or we can actually enter the
expressions (e.g., 1.9-0.0063) and the calculator will simplify the values.
Figure 86 shows the status of the screen after all values have been entered. |
Figure 87

| By pressing the  key we leave the RANGE screen and move
to the GRAPH screen shown in Figure 87. key we leave the RANGE screen and move
to the GRAPH screen shown in Figure 87. |
Figure 88
| Pressing the  key moves the calculator into
TRACE mode. Figure 88 shows that we are at the point (1.9,3.7) and that we are
tracing the equation number 1. We are at that point because it is the center of the
newly created screen. key moves the calculator into
TRACE mode. Figure 88 shows that we are at the point (1.9,3.7) and that we are
tracing the equation number 1. We are at that point because it is the center of the
newly created screen. |
Figure 89

| We can shift the TRACE focus from equation 1 to equation 3 by
pressing the  key 2 times. Figure 89 shows that we are
still at the same point, but now we are on equation 3. This must be the point of
intersection since it is a point on both lines. key 2 times. Figure 89 shows that we are
still at the same point, but now we are on equation 3. This must be the point of
intersection since it is a point on both lines. |
Figure 90
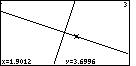
| Figure 90 is the result of moving the TRACE marker to the right. At each step of the
move the coordinates change. It is important to note that the coordinates are those
of the real line, not of the selected pixels. After all, a close inspection of the line for
equation 3 reveals that, in Figure 90, it is made up of groups of three horizontally
adjacent pixels. Remember that the equation has a slope of 1/3. If we have
created a screen with equal horizontal and vertical spacing, then it should take
three horizontal pixels for each vertical one. However, as the TRACE marker moves across
the three pixels, the y-coordinate will show the appropriate changing value. |
Figure 91

| Pressing  from Figure 90 will cause the
TRACE marker to move to the first equation, as is shown on Figure 91. from Figure 90 will cause the
TRACE marker to move to the first equation, as is shown on Figure 91. |
That is all for this page. Hopefully, it has given you a chance to do some graphing and
to learn to use the various keys and options on the calculator.
There are many other graphing features on this calculator. Their explanation and
illustration will have to wait for another page.

 key.
key.
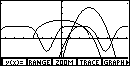
 key.
This selects the first screen menu item, the item at the bottom of the
key.
This selects the first screen menu item, the item at the bottom of the  keyscreen just
above the
keyscreen just
above the  key. That first menu item, y(x)=,
brings up a display of all of the functions that are currently defined for
graphing on the calculator. Each separate function starts with y index = such
as y1= or y2=.
If there is nothing after the equal sign then there is no function assigned there.
key. That first menu item, y(x)=,
brings up a display of all of the functions that are currently defined for
graphing on the calculator. Each separate function starts with y index = such
as y1= or y2=.
If there is nothing after the equal sign then there is no function assigned there. 
 key. The result is shown in Figure 4.
Note that the background black rectangle surrounding the equal sign in the first
equation has disappeared. This is an indication that this equation has been de-selected.
key. The result is shown in Figure 4.
Note that the background black rectangle surrounding the equal sign in the first
equation has disappeared. This is an indication that this equation has been de-selected.
 key. This puts the blinking cursor
onto the negative sign in the second function, as shown in Figure 5.
key. This puts the blinking cursor
onto the negative sign in the second function, as shown in Figure 5. 
 key. The result is shown in Figure 6.
key. The result is shown in Figure 6. key, clear that function with the
key, clear that function with the
 key, move down again via
another
key, move down again via
another  key, and
clear that function with the
key, and
clear that function with the  key.
key.
 key and then the
key and then the  key.
That takes us to the GRAPH screen.
Figure 7 represents the conclusion of our efforts to clear out all of the
pre-existing functions. We now have a clear graph.
key.
That takes us to the GRAPH screen.
Figure 7 represents the conclusion of our efforts to clear out all of the
pre-existing functions. We now have a clear graph. 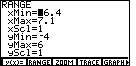
 key. This brings up Figure 8, although
your calculator may have different values displayed. Note that the
blinking cursor is on the negative sign of the value -6.4 in Figure 8.
key. This brings up Figure 8, although
your calculator may have different values displayed. Note that the
blinking cursor is on the negative sign of the value -6.4 in Figure 8.


 to set the lowest displayed x-value, the x-value
at the left edge of the screen, to be -10. This has been done for Figure 9.
to set the lowest displayed x-value, the x-value
at the left edge of the screen, to be -10. This has been done for Figure 9. key when we enter this value.
We want a negative value. We do not want to subtract.)
key when we enter this value.
We want a negative value. We do not want to subtract.)
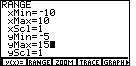


 keys.
The display should match Figure 13.
keys.
The display should match Figure 13.



 .
This produces the changed screen shown in Figure 17.
.
This produces the changed screen shown in Figure 17.


 key 3 times. This leaves the
blinking cursor covering the 5, as in Figure 20.
key 3 times. This leaves the
blinking cursor covering the 5, as in Figure 20.



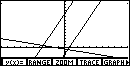
 key. Figure 25 shows that ZOOM menu
under the usual GRAPH menu. Note that there is a small arrow at the right end of
the rightmost option. This arrow indicates tht there are more options in the menu and
that we will have to use the
key. Figure 25 shows that ZOOM menu
under the usual GRAPH menu. Note that there is a small arrow at the right end of
the rightmost option. This arrow indicates tht there are more options in the menu and
that we will have to use the  key to see those additional options.
key to see those additional options.
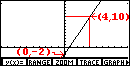
 key we will select and perform
this option. The screen will be rewritten, as in Figure 26, with the new RANGE settings.
Notice in Figure 26 that the x-axis (the horizontal line) has
moved to the middle of the screen. This is different from what we had in
Figure 25. We can see the cause of this change if we return to
the RANGE screen so that we can review the settings there.
key we will select and perform
this option. The screen will be rewritten, as in Figure 26, with the new RANGE settings.
Notice in Figure 26 that the x-axis (the horizontal line) has
moved to the middle of the screen. This is different from what we had in
Figure 25. We can see the cause of this change if we return to
the RANGE screen so that we can review the settings there.
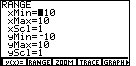






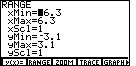



 and
and  keys. I have done that
in Figure 37 until I have the pointer at (-0.3,0.4) as noted by the coordinates at the
bottom of the screen. This point will be the upper left corner of the box that I will draw.
keys. I have done that
in Figure 37 until I have the pointer at (-0.3,0.4) as noted by the coordinates at the
bottom of the screen. This point will be the upper left corner of the box that I will draw.

 key. The calcualtor responds by
placing a small square at the corner point selected.
key. The calcualtor responds by
placing a small square at the corner point selected.

















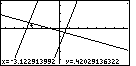






 key. In Figure 63 we can see the two levels of the menu.
We want to look at the values on the RANGE screen. Therefore, we press
key. In Figure 63 we can see the two levels of the menu.
We want to look at the values on the RANGE screen. Therefore, we press




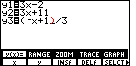
 .
The blinking block cursor changes to a blinking underline cursor
to indicate that we are in INSERT mode. Figure 68 has been augmented with
a red parenthesis to remind us that the parenthesis character is still there.
.
The blinking block cursor changes to a blinking underline cursor
to indicate that we are in INSERT mode. Figure 68 has been augmented with
a red parenthesis to remind us that the parenthesis character is still there.