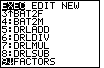
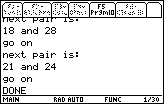
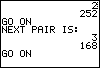Program to find factor pairs of a number
Any printout of this page should be done in LANDSCAPE mode.
In class we worked on methods for factoring polynomials.
One of those methods was called "splitting the middle term".
For example, in the problem,
15x2 + 19x - 10
we start the process by multiplying the 15 and the -10 to get -150.
Then, we look for a pair of numbers that multiply to give 150 and that
have a difference of 19, the coefficient of the middle term.
(We want a difference rather than a sum of 19 because we have
different signs on the first and last terms of the original problem.)
We can make a list of pairs of numbers that multiply to give 150, such as
150 * 1 = 150
75 * 2 = 150
50 * 3 = 150
25 * 6 = 150
15 * 10 = 150
and then we look through that list to find where we can get a difference of 19.
In this case, we see that 25 - 6 gives 19. Therefore, we rewrite the problem as
15x2 + 25x - 6x - 10
Then we factor the first two terms, and the last two terms to get
5x(3x + 5) - 2(3x + 5)
which allows us to factor out the common binomial, (3x+5),
to get
(5x - 2)(3x + 5)
This process works well, but it depends upon us being able to find pairs of numbers that
are factors of some generally large value. For example, in the problem
24x2 - 10x - 21
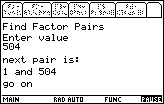
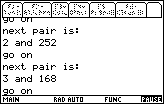
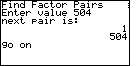
the first step is to multiply 24 times -21 to get -504.
Then, we need to find pairs of values that multiply to give 504 and whose
difference is -10 (the coefficient of the middle term).
Unfortunately, 504 has many factors. It is a challenge to come up with the list of pairs of factors.
When we saw this in class, we noted that it would be helpful if we could get our calculators to
find those pairs of factors. To that end, we created the following program:
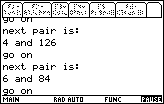
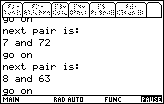
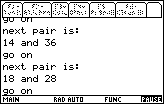
Below is a table showing the output for the various forms of the program.
| TI-83 Example | TI-85 or TI-86 Example |
TI-89 Example |
 |
 |
 |
©Roger M. Palay
Saline, MI 48176
August, 2010