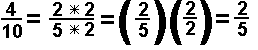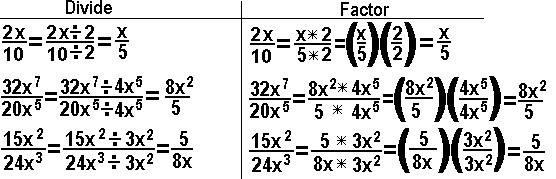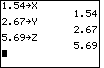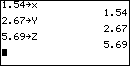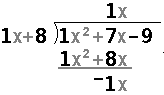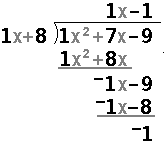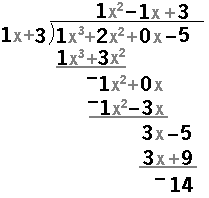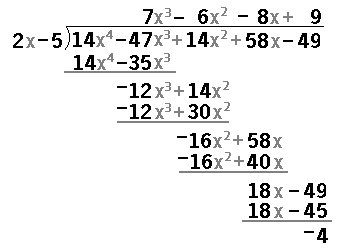General NOTES for Math 169
Fifth Edition
Chapter 6

Introduction to Detailed Notes

This is a set of notes that have been made on reading the textbook. There is no real attempt to have comments on absolutely everything in the book noted here. At the same time, there is supplementary material here that is not in the book.

After writing out the notes for the first few sections, it has become clear that there is a tendency to make this a "teaching" document. As much as possible, efforts will be made to not do this. Rather, if there is teaching material to be presented then that will be done in separate pages, with pointers inserted here.

Chapter 6: Rational Expressions

6.1 Reducing Rational Roots

Page 336: I find the notation in box #2 at the bottom of the page to be unrealistic and confusing. First of all the text in the box should read

There are two equivalent approaches to reducing rational numbers. On the one hand we talk about dividing the numerator and the denominator by the same value. We could illustrate such a case by looking at the rational number 4/10. We could divide both numerator and denominator by 2 to produce

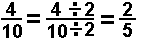On the other hand we talk about factoring out common values. The work for such an approach would be

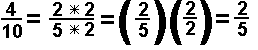
Then, the remainder of the box should hold the example, each done both ways, with a clear distinction between the two methods, as in

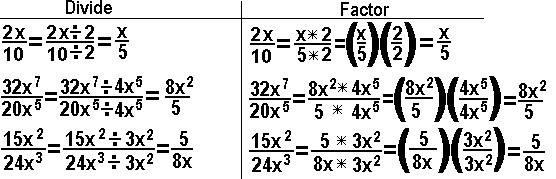We can not get the TI-86 calculator to do these kinds of problems in general. However, as we have been doing throughout the text, we should use the calculator to verify our answers. For example, problem Q3f on page 338 starts with the expression:

18x³y²z

32xy²z⁴

and the simplification is

9x²

16z³

We can check our answer by choosing some strange values for "X", "Y", and "Z", and then using our calculator to evaluate the original expression and evaluate our simplification expression. We need to get the same value for both. The table below gives the screen images for doing this.

TI-83 screen images	explanation	TI-86 images
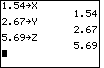	First we assign some strange values to the variables. Note that we are using a lower case "x" on the TI-86.
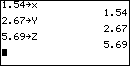	Then we evaluate the two expressions.

6.2 Multiplication and Division of Rational Expressions

This section seems to flow fairly well. When we finally get to the "long division" algorithm on page 348, I have a slightly different form for writing out the long division problems. In particular, for the problem

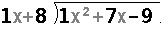we ask "What do I need to multiply x+8 by to get x²?" The answer is 1x. Therefore, I write the 1x in the quotient, in the same column as the "x" in the dividend. This produces

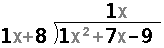Then we multiply the "1x" if the quotient times the "1x+8" of the divisor to produce "x²+8x", which we then subtract from the dividend, as in

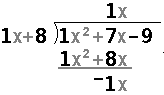Then we bring down the next term, "^–9", and continue the process to produce

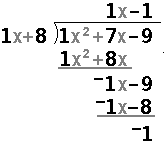This is the same algorithm that is used in the book, except that I keep the variables lined up. That is, in my approach, there is a column that contains the x² terms, a column for the x terms, and a column for the constant terms.

It is even easier to see this approach if we look at the problem from the instructional box #7 on page 350. My version would be

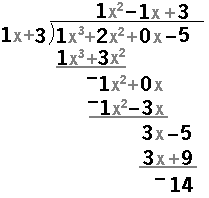Again, I have a column for the x³ terms, a column for the x² terms, a column for the x terms, and a column for the constant terms. We can consider an additional example, not in the book:

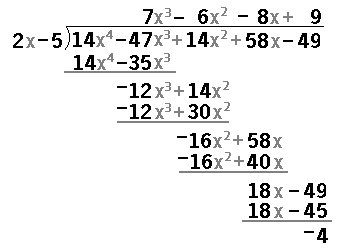
The process of doing this division of polynomials is well defined. We can write computer and/or calculator programs to do this task. The TI web site has an archive of programs to do many different tasks. One such program is the POLYDIV program for the TI-83. The POLYDIV on the TI-83 page illustrates the use of that program. Another program, and one that does even more than polynomial division, is the Poly3 program for the TI-85 and TI-86. The Poly3 on the TI-86 page illustrates the use of this program to do polynomial division.

The programs discussed above do polynomial division, but they only provide the answer. It is possible to construct programs that actually produce the various subproducts and intermediate remainders in our long division algorithm. The POLYDIV1 program for the TI-83 and the polydiv program for the TI-85, the TI-86, the TI-89, and the TI92 Plus do just that. The web pages POLYDIV1 for the TI-83, polydiv on the TI-86, and polydiv on the TI-89 illustrate these programs.

6.3 Addition and Subtraction of Rational Expressions

On page 353 the book presents two methods for finding the sum or difference of two rational numbers, namely, the least common denominator method or the cross-product method. These are different approaches, but they are not really different methods. To add (or subtract) two rational numbers they must have the same denominator. Actually, we can see this by looking at all the steps that go into doing 2/3 + 4/5:

In this example, the two original denominators, 3 and 5, are relatively prime. That is, the two numbers do not have any common factors, other than 1. In such a situation, the two "methods" are idenitcal.

In a case where the two denominators are not relatively prime, as in

7/10 + 4/15 then the advantage of the least common denominator method is that we use smaller numbers: (3/3)(7/10) + (4/15)(2/2)
21/30 + 8/30
29/30 The disadvantage is that we have to find the least common denominator. Note that we may have to reduce the answer, although we did not have to so so in the example above.

With denominators that are not relatively prime, the cross-product method produces larger numbers that will always require the extra steps of "reducing the final answer". In our example we have

(15/15)(7/10) + (4/15)(10/10)
105/150 + 40/150
145/150
(29/30)(5/5)
29/30 The advantage of the cross-product method is that it is a mechanical process. We use whatever denominators we are given. We do not have to find the least common multiple.

The book goes on to demonstrate the addition and subtraction of rational expressions using the same methods tht we used for adding and subtracting numbers. Again the to methods are not really different. We need to multiply each of the two given rational expressions by "1" in the form of a polynomial divided by itself. For the least common denominator approach we search to find the smallest forms of "1" that will give us the desired result. In the cross-product approach we use the expressions that are given as the denominators and we suffer the consequence that we need to reduce the resulting answer.

Although the TI-89 and TI-92 calculators can correctly add or subtract two rational expressions, the same is not true for the TI-83, TI-85, and TI-86. The best that we can do with those calculators is to check our work. As we have done in other situations before, we can assign some strange value to the variables in the problems. Then we can find the value of the original problem and compare that to the value of the answer. The two values must be the same. In a simple case, for question Q5b on page 356, if we assign the value 2.0587 to M then we can use the TI-83 to evaluate the original problem

2m + 1		m – 5
	–
6		4

which we have done in the steps illustrated as

Because the two expressions produce the same result, namely 1.632391667, we can be confident (though not certain) that our answer is correct.

In the more complex case of Q18e on page 368,

x + y		x – y
	+
x² + 2xy – 15y²		x² – 25y²

we can assign strange values to X and Y, as in

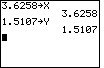Then we can evaluate the original problem, as in

Finally, we can evaluate the answer that we found, as in

Again, the two evaluations produce the same number. Therefore, we can be confident (though not certain) that our answer is correct.

6.4 Complex Fractions

The amterial in this section is fairly clear. Again, although the book tries to explain two methods, they are really the same. These problems tend to require us to "grind out" the solution. We can use our calculator to check our answers as we have done above.