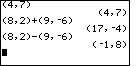


 .
Then, when we press
.
Then, when we press  the calculator accepts our value and redisplays
it on the right side of the screen.
the calculator accepts our value and redisplays
it on the right side of the screen.
Figure 1 continues with the problem (8 + 2i) + (9 – 6i) which we represnt via
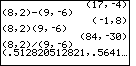
 key to shift the display to the right.
key to shift the display to the right.

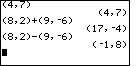
|
Figure 1 starts with an example of a complex number, namely 4+7i, but which we need to represent as
(4,7). We generate that value via the keys
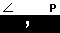   .
Then, when we press .
Then, when we press  the calculator accepts our value and redisplays
it on the right side of the screen. the calculator accepts our value and redisplays
it on the right side of the screen.
Figure 1 continues with the problem (8 + 2i) + (9 – 6i) which we represnt via |

|
Now we will examine the multiplication and division of complex numbers.
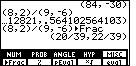
In Figure 2 we can see that
 key to shift the display to the right. key to shift the display to the right.
|

|
Now we can see the rest of the answer, namely,
|

|
Figure 4 restates the division problem but with the |
The problems presented so far have involved complex numbers of the form (a,b) where a and b have been rational numbers. However, the definition of complex numbers only requires that a and b be real numbers. Thus, we could have a problem such as
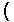

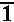
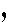
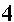

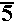
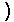
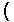

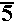
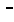
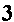

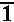
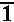
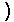
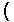
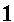
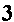

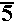
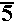
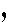
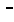
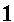
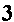
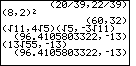
|
In Figure 5 we start by demonstrating the squaring a complex number. This has nothing to do with the discussion above,
but it does provide a small example.
Then, Figure 5 shows how we enter the original problem and follow that by our computed answer. As we can see, in both cases the calculator evaluates the expressions to the same approximations.
|
©Roger M. Palay
Saline, MI 48176
August, 2000