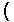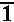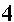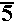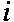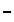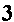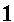Figure 1
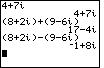
| Figure 1 starts with an example of a complex number, namely
4+7i. We generate that value via the keys
   .
Then, when we press .
Then, when we press  the calculator accepts our value and redisplays
it on the right side of the screen. the calculator accepts our value and redisplays
it on the right side of the screen.
Figure 1 continues with the problem
(8 + 2i) + (9 – 6i)
which the calculator computes to be
17 – 4i
We follow that by the subtraction problem,
(8 + 2i) – (9 – 6i)
which the calculator computes to be
–1 + 8i
Note that the parentheses were not needed in the addition problem. However, at least the second
set of parentheses are required in the subtraction. If we did not include them then the problem
would have been evaluated as
8 + 2i – 9 – 6i
8 + 2i + –9 + –6i
–1 – 4i
|
Figure 2

|
Now we will examine the multiplication and division of complex numbers.
Again, for these problems the parentheses are essential. In Figure 2
we can see that
(8 + 2i)(9 – 6i)
is evaluated to be
84 – 30i
which is the value that we should expect. However,
(8 + 2i) / (9 – 6i)
is evaluated as
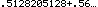 where the three dots at the right end of the screen indicate that there is more to the answer.
We use the
where the three dots at the right end of the screen indicate that there is more to the answer.
We use the  key to shift the display to the right. key to shift the display to the right.
|
Figure 3

| Now we can see the rest of the answer, namely,
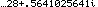 If we could put the two pieces together we would have
If we could put the two pieces together we would have
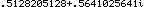 This still looks pretty strange. To do the problem on paper we would multiply
numerator and denominator by the complex conjugate of the denominator, in this case by
(9 + 6i)
The result would produce a denominator that is 92–6i2, or
81+36, or 117.
The numerator would be 8(9)+8(6i)+(2i)9+2i(6i) which we simplify first to
72+48i+18i–12, and then to 60+66i.
Thus, the entire answer is (60+66i)/117, or 60/117 + 66i/117,
which we can reduce to
20/39 + 22i/39. And, we note that 20/39 is approximately 0.5128205128 and
22/39 is approximately 0.5641025641. It seems that we have the correct answer, but we would
prefer that the calculator provide it in fractional form.
This still looks pretty strange. To do the problem on paper we would multiply
numerator and denominator by the complex conjugate of the denominator, in this case by
(9 + 6i)
The result would produce a denominator that is 92–6i2, or
81+36, or 117.
The numerator would be 8(9)+8(6i)+(2i)9+2i(6i) which we simplify first to
72+48i+18i–12, and then to 60+66i.
Thus, the entire answer is (60+66i)/117, or 60/117 + 66i/117,
which we can reduce to
20/39 + 22i/39. And, we note that 20/39 is approximately 0.5128205128 and
22/39 is approximately 0.5641025641. It seems that we have the correct answer, but we would
prefer that the calculator provide it in fractional form.
|
Figure 4

| Figure 4 restates the division problem but with the 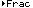 symbol appended to the end of the command. The result is exactly as we had determined above.
symbol appended to the end of the command. The result is exactly as we had determined above.
NOTE, however, that we need to interpret the result carefully. It is given as
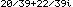 but we need to recognize that this is meant as
but we need to recognize that this is meant as
 even though the calculator does not supply the extra parentheses. In particular, the result has a fraction times
i, which really means, in this case 22i/39.
even though the calculator does not supply the extra parentheses. In particular, the result has a fraction times
i, which really means, in this case 22i/39.
|
Figure 5

| One of the problems related to the calculator implementation of complex numbers is the fact that we
really do need to add the parentheses in these problems. If we forget them, the calculator will produce
an answer, but it will be the answer to a different problem.
If we repeat out previous problem, but this time remove the parentheses,
then the calculator responds as in Figure 5. The
calculator is really performing the problem
8 + (2i/9) – 6i
which is 8 – (52/9)i. |
Figure 6

| In Figure 6 we demonstrate squaring a complex number. |
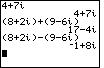



 .
Then, when we press
.
Then, when we press  the calculator accepts our value and redisplays
it on the right side of the screen.
the calculator accepts our value and redisplays
it on the right side of the screen.

 key to shift the display to the right.
key to shift the display to the right.