On this page we will look at a number
of examples of one sample hypothesis testing.
In particualr, we will look at four
different cases outlined in the following table.
Figure 1
|
We see that the sample mean, `85.284` is indeed greater than the
`H_0: mu=77.7`, but is it so big that we will reject `H_0` in a process that will
be correct 99% of the time? To find out, we will compute a test
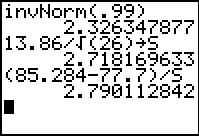
statistic, `z=(barx - mu)/(sigma/sqrt(n))=(85.284-77.7)/(13.86/sqrt(26))`
and then examine that test statistic.
Since
we know that the distribution of the sample means is
normal, we use invNorm.
In this case we look at invNorm(.99) because we want
a critical value that represents being too high to be reasonable.
Such a value will have 99% or the area under the normal curve to its left.
We see that the critical value is 2.326.
Then, we compute the test statistic. In Figure 1 we do this in two steps.
First we get the eventual denominator and store it in S. Then
we compute `(barx-mu)/S` as the test statistic 2.790.
Remember that our critical value represented the highest value
that we would tolerate and still accept `H_0`. This test statistic
is even larger than the critical value. Therefore, we reject
`H_0`.
|
Figure 2
 |
The decision that we reached in Figure 1 was based on having the critical value.
The P-value approach has us look to see just how much area
is to the right of the computed test statistic.
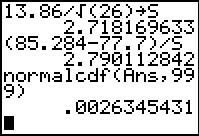
We can do this via the normalcdf(Ans,999) command.
It returns the value .002634 to indicate that there is less than
the 0.01 that we were willing to accept.
In the P-value approach, we see that if `H_0` were true, getting a sample
with a mean as large as, or larger than, ours would be extremely rare.
More rare than the 0.01 we were willing to accept. Therefore,
using this method we would reject `H_0`.
|
Figure 3
 |
We have accomplished a great deal in Figures 1 and 2, but they depend upon our
performing many computations. The calculator has a special
command that will do almost all of this for us. This is the
Z-Test... command found in the STAT menu under the TESTS
sub-menu.
|
Figure 4
 |
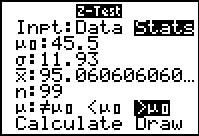
The Z-Test... command brings up
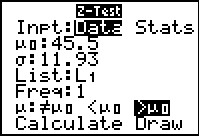
the data input screen shown in Figure 4.
The first thing that we need to change here is that
we do not have Data, we have Stats.
|
Figure 5
 |
Move the highlight to the Stats field and press
 . .
|
Figure 6
 |
Then move down the form to enter the values:
`u_0` is the hypothesized mean, 77.7;
`sigma` is the population standard deviation;
`barx` is the sample mean;
`n` is the sample size;
and we want to select `>mu_0` as our test.
Then move the highlight to the Calculate option.
Press  to have the calcualtor perform the test.
to have the calcualtor perform the test.
|
Figure 7
 |
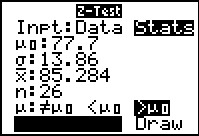
Here is the result of that test.
The calculator echoes the test, `U>77.7`,
produces the test statistic `z=2.790112842`,
produces the P-value of that statistic, `p=.00263454431`,
echoes the sample mean `barx=85.284` and the sample size `n=26`.
It just remains for us to say that the P-value is samller
than the allowed 0.01. Therefore, we reject `H_0`.
|
Figure 8
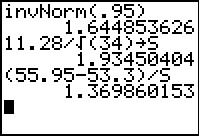 |
The problem specifies that we will tolerate a 10% error.
Therefore, we want critical values that
have only 5% below and 5% above them.
We use the invNorm(.95) to get those values.
Recall that the normal distribution is symmetric.
Therefore, our two values are `-1.644` and `1.644`.
Our test statistic needs to be outside these values to reject the null hypothesis.
Again we compute the test statistic in two steps.
The result is 1.369 and this is not outside the critical values.
Therefore, we accept `H_0`.
|
Figure 9
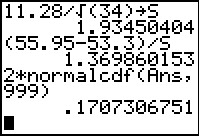 |
Alternatively, we could use normalcdf
to find the area to the right of the test statistic.
However, we need to remember that we also need to add in the
area to the left of the opposite critical value. Again, using the symmetry of the distribution,
we compute the total area as 2*normalcdf(Ans,999).
The result, 17.07 is larger than the limit that
the problem statement imposed. Therefore, we accept `H_0`.
|
Figure 10
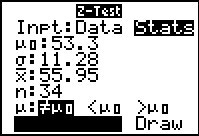 |
The other approach to this problem is to use the Z-Test... command
which opens the input form shown in Figure 10 after we have entered the
values from this problem. Highlight the Calculate field
and press  . .
|
Figure 11
 |
The results, identical to those we found in the longer appraoch,
are shown in Figure 11.
|
Figure 12
 |
The challenge in Case II is that we do not know the standard
deviation in the underlying population. In this case we need to use the
sample standard deviation whcih changes the distribution of
the sample means to a
t-distribution, not a normal distribution.
Following the process used before, we find the
critical value. In this case we may be able to use the
invT( command. (This cammand is available on TI-84's with
the newer operating system. If it is not available on your calcualtor you may
use the INVT program illustratied in Figure 13).
|
Figure 13
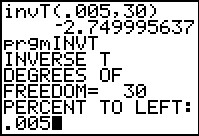 |
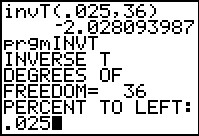
The invT( command, if it is available, has two arguments, the area
measure and the number of degrees of freedom. From the problem statement
we see that we wnat the area under the curve to be 0.005 and that we have
30 degrees of freedom (one less than the sample size). The result is the
value `-2.749995637`.
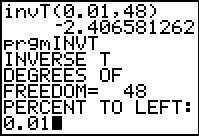
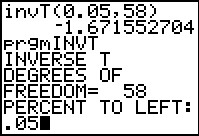
If the invT( command is not available we can use the INVT
program. It asks for the number of degrees of freedom and the percent of
area to the left.
The output from the program appears in Figure 14.
|
Figure 14
 |
The answer from the program is not wuiote the same as that from the built-in function,
but the difference is minor.
|
Figure 15
 |
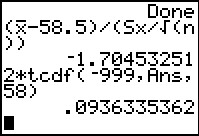
Returning to our solution, we compute the test statistic,
`t=(barx-mu)/(s_x/sqrt(n))=(13.741-18.6)/(10.02/sqrt(31))`.
On the calcualtor we have computed this in two steps,
first computing the denominator, then the quotient.
The result `-2.69997675` is not as extreme as was our
critical value so we accept `H_0`.
Alternatively, we could have use the P-value approach where
we compute the area outside of the test statistic.
We do that with the tcdf( command, wich also requires the degrees of freedom.
Again, the result is the 0.0056425488 which is larger than the allowed
0.005 in the problem statement. On that basis we
accept `H_0`.
|
Figure 16
 |
In the TESTS sub-menu of the STAT menu there is
a command that does all of this for us, namely, the T-Test...
command.
|
Figure 17
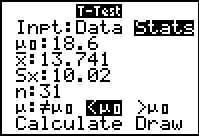 |
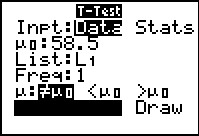
The T-Test... command opens the input form shown in Figure 17.
We need to be sure that the Stats option is selected
and then we supply the
rest of the values as given in the problem, including setting the
option for testing the `Calcualte option and press
 . .
|
Figure 18
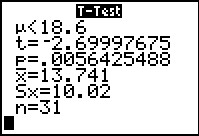 |
Figure 18 gives the results of the command, including the
t-statistic and the P-value.
The result is the same as we obtained in the
longer approach given above.
|
Figure 19
 |
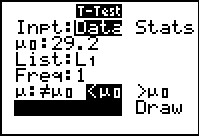
This second Case II example, the only real change is that
we are now looking at a not equal to
alternative hypothesis. Therefore, just as we did back in Figure 8,
we have to spread the 5% both above and below the supposed mean.
Therefore, we find the critical value, using the t-distribution
with 36 degrees of freedom, to have 2.5%
on each side.
Again, in case the invT( command is not available, we can use the
INVT program.
|
Figure 20
 |
We get essentially the same value.
|
Figure 21
 |
Now we compute the t-statistic as before,
producing `-2.600066356`, which is outside of the critical value,
resulting in a decision to reject `H_0`.
Also, we could have computed the P-value,
remembering to double it, to find that it is
0.0134334558 which is far below our threshhold of 0.05.
|
Figure 22
 |
We could have done the problem using the
T-Test... command. We fill in the
values from the problem.
|
Figure 23
 |
The computed results are given in Figure 23.
|
Figure 24
 |
Case III is similar to Case II, except that we are given the sample, not the
sample statistics.
This is not much of a problem because we can compute those values.
First, we generate the data.
|
Figure 25
 |
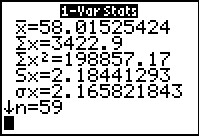
Then, we obtain the 1-Var Stats.
|
Figure 26
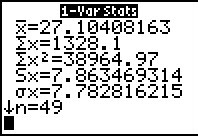 |
The values are given here, and we could write them down and re-enter them
later, but we do have an alternative.
|
Figure 27
 |
As has been our pattern, we first find the critical value
either via the invT( command or the
INVT program.
|
Figure 28
 |
Again, the program produces similar results.
|
Figure 29
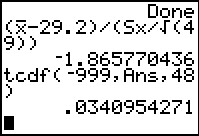 |
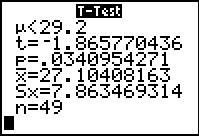
In Figure 29 we compute the t-statistic using the variables
from the VARS menu, Statistics... sub-menu.
The result, `-1.865770436` is not as extreme as is
the critical value. Therefore we accept the null hypothesis.
If we compute the P-value we see that it is not strange enough
to reject the null hypothesis, which is why
we accept it.
|
Figure 30
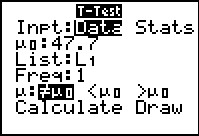 |
The power of the calculator is even more apparent when we use
the T-Test... command here. First, we change the setting to
Data. This changes the other available options.
We just have to tell the command the value to test, the location of the
data, and our choice for the kind of test we are running.
|
Figure 31
 |
Once the values have been set, we highlight the Calculate
option and press  . .
|
Figure 32
 |
The results are displayed in Figure 32.
|
Figure 41
 |
Case IV looks at a hypothesis test for a population proportion.
We can start by generating the data.
|
Figure 42
 |
Once the data is generated, and noting that the
characteristic of interest is
the value 2. All that we really need is to
find the number of items and the number of items that are 2.
Clearly, one way to do this is to run the
COLLATE2 program. We are not really interested in the various
statistics that
COLLATE2 displays, but we do want to see the table
of values along with the count of each item.
COLLATE2 is really overkill for this problem. We will look at an
alternative method in Figure 51.
In order to speed up the process,
we have a revision of COLLATE2 program.
It is not necessary to use the revised
version since it only gives the user a way
to skip the slow output of values.
|
Figure 43
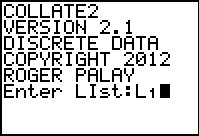 |
In Figure 43 we can note that we are running version 2.1 of the program.
|
Figure 44
 |
We note here that there are 87 values.
Also, we see the change in the program
to allow the user to opt out of the display of values.
|
Figure 45
 |
After the program completes we move to the Stat Editor.
Here we see that item 2 has a frequency of 24.
This is all we really need.
|
Figure 46
 |
As usual, we compute the critical value.
Note that we have returned to using the normal distribution.
This is because, given the restriction we palce on our sample sizes and
the related number of required items in the groups, the distibution
of the test statistic will be approximately normal.
Another important point, when we compute the denominator of the test statistic we use the proportion
from the hypothesis, not the proportion in the sample.
[This is different than when we computed the confidence intervals for proportions.]
The z-statistic is 1.016492056 which is not as extreme as
is the critical value. Therefore, we accept the null hypothesis.
|
Figure 47
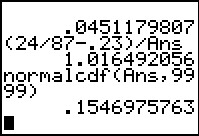 |
In Figure 47 we have computed the area outside of the critical value.
It provides a different approach to the problem but produces
the same result, we do not reject the null hypothesis.
|
Figure 48
 |
The TESTS sub-menu of the STAT menu has yet another
command, 1-PropZTest..., the command that is appropriate
for this case.
|
Figure 49
 |
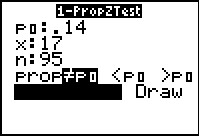
There are few values that we need to supply here.
`p_0` is the proportion in the null hypothesis.
`x` is the number of items in the sample with the characteristic of interest.
`n` is the sample size.
And then we have the options for the style of the
alternative hypothesis.
|
Figure 50
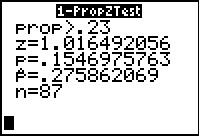 |
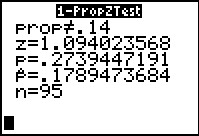
The results are shown in Figure 50. The same values
that we computed the long way.
|
Figure 51
 |
As noted in the discussion along side of Figure 42,
once the data is generated, we just need to get a count of the
characteristic of interest. In Figure 42 we used COLLATE2
to do this. Here we demonstrate an alternative.
We will set up a histogram that will take care of the entire
problem. We know that we will have values 1, 2, 3, and 4.
We want a histogram that has one column for each value.
Set Plot1
be a histogram.
|
Figure 52
 |
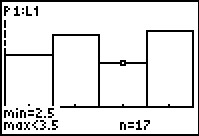
Set the WINDOW valeus to get our separate columns.
|
Figure 53
 |
Use  to move to the Graph.
Use to move to the Graph.
Use  to start the Trace.
Then use the cursor key to move the highlight to the column
of interest, in this case the second column.
Note that the number of items in that column is given at teh bottom of the
screen. to start the Trace.
Then use the cursor key to move the highlight to the column
of interest, in this case the second column.
Note that the number of items in that column is given at teh bottom of the
screen.
We will use this approach for the next example.
|





 .
.

 to have the calcualtor perform the test.
to have the calcualtor perform the test.




























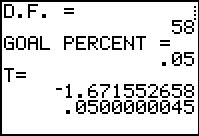














 to move to the Graph.
Use
to move to the Graph.
Use  to start the Trace.
Then use the cursor key to move the highlight to the column
of interest, in this case the second column.
Note that the number of items in that column is given at teh bottom of the
screen.
to start the Trace.
Then use the cursor key to move the highlight to the column
of interest, in this case the second column.
Note that the number of items in that column is given at teh bottom of the
screen.