We need to start with some data. We will generate a list of data on the calculator using GNRND4 with Key 1=192338704 and Key 2=9000524. That list will be the same numbers that appear in the following table: Thus, our problem will be to generate a frequency table for the data in the list above.

Before we even start the problem we need to spend a moment explaining why we are treating this as continuous data. Clearly these are integer values. Individually they do not look any different from the values that we used when we did our analysis of discrete data before. However, in the 88 values given above we have 80 different values. That means that at least 72 values appear just once. It would not tell us very much if we were to use COLLATE2 to find all of those different values and to look at teh frequency of each. Almost all will have a frequency of 1. Therefore, we need a different approach. We treat the values as continuous. We will divide the range of values into even intervals. Then we will count the number of items in each interval.

Figure 1	Figure 1 starts with a run of the GNRND4 program where we have entered the two key values given above.
Figure 2	In Figure 2 we can see the start of the list of values. We recall that the list is created by GNRND4 as L1. Also note that we had pressed the key to allow the program to terminate before we took this image of the screen.
Figure 3	For the sake of being able to return to the original lsit, we will make a copy of the list. The keys to do this are . Then we use to have the calculator perform the command.
Figure 4	To sort the values in L2 we need to get the proper command. Press to move to the LIST menu. Then use the key to open the OPS sub-menu. The option we want is the first one, Sort(. Therefore, press to select that option and paste it onto the home screen.
Figure 5	We finish the command by pressing and we get the calculator to perform the command by pressing . Once that is done, since the items in L2 are now in ascending order, we can find the lowest value by looking at the contents of the first element of L1. We press the sequence to geneerate the command. We press to have the calculator perform it. The result is in Figure 6.
Figure 6	Now we know that the lowest value is 333. We could find the highest value if we asked the calculator to display the last position in L2. We could count the values in the table above, or we could just ask the calculator to tell us the size of L2. The latter alternative is more appealing. the command we want is dim(L2).
Figure 7	We return to the LIST menu, the OPS sub-menu, and select the dim( option.
Figure 8	We complete the command with and execute it with . The calculator responds with 88 meaning that there are 88 values in L2. Therefore we construct the command and press to have the calculator tell us the value stored in the last element of L2. the response is 728. We can then ask the calculator to find the range by getting the difference of the high and low values. with a range of 395 we might decide to have classes that are 50 wide, starting at 330. That way, with 8 classes we will cover the entire range of values.
Figure 9	We want to examine the values in L2. We can use the STAT Editor to do that, but, given our earlier use of some lists produced by COLLATE2, it would be good to reset the editor to display the built-in lists. We return to the STAT menu and SetUpEditor option by pressing the key.
Figure 9a	Once the SetUpEditor command has been pasted on the screen, we press to perform the command. Then, to move to Figure 10, we press to re-open the STAT menu and, from there, press to open the editor.
Figure 10	Once in the editor, we move to the second column by using the key. This screen shows the sorted values in L2. We know that we want the first "class" of values to run from 330 to just before 380. Looking at these values we see that we have 6 items (333, 341, 343, 345, 373, and 379) in this class. Then we can move down the list to see more values.
Figure 11	Our next class has limits 380 to just before 430. There are 4 items in this class (400,403, 407, 425). We should note that we could have used the index values, shown for the highlighted item as the bottom of the screen, to produce the number of items between two items. Thus, if we know the index of the first item in the class and the index of the last item in the class we can compute the number of items in the class as class size =(index of high value) - (index of low value) + 1 For example, the high value in the second class was 425. That value is in the 10th position. The low value in the second class was 400 and it was in the 7th position. Thus class size = (10) - (7) + 1 class size = 4
Figure 12	Here are more items. This is a long list and we have many more such screens to examine in this brute stength and awkwardness approach of counting items.
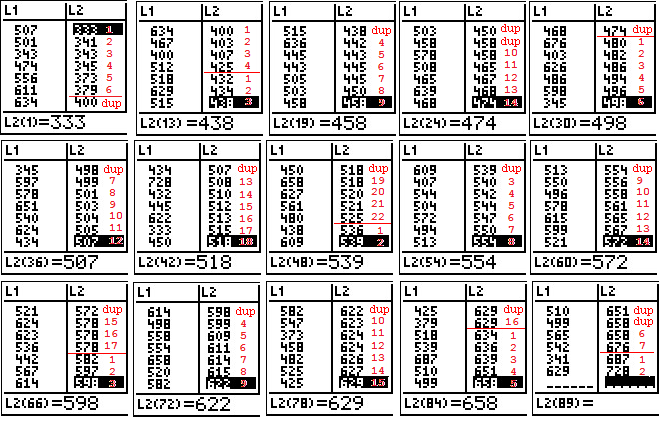
Figure 13 Here is a compilation of portions of all the screens that one would look at to see the entire list of valeus. The images here have been amended to have, in red, the cut points for the different "classes" that we want and a sequential number to count the items in each class. Note that items that are duplicated from one screen image to another are marked as "dup".

Looking at the values that were displayed in the numerous screens we could compose a frequency table for the data. In particular we could construct

Figure 14	An alternative approach to getting the values for the frequency table is to let the calculator create a histogram of the data and then we can manipulate the WINDOW settings to correspond to the class limits that we want to use. To do this we start by reviewing the plot settings. Press to get the STAT PLOT screen shown if Figure 14. There we see that Plot1 is "On" but it is set to use L3 and we have our data in L1 (and a copy is in L2). To change the setting we press .
Figure 15	Figure 15 shows the current settings for Plot1. Use the cursoe keys to move the highlight to the value after Xlist: as shown in Figure 16.
Figure 16	Now we can change this setting. To change it to L1 press . This result is shown in Figure 17.
Figure 17	The settings are as we want. We can move directly to the ZOOM menu by pressing the key.
Figure 18	The option we want is ZoomStat and we need to move down to that option. Selecting this option, when we have a Plot set to do as Historgram as we do, will cause the calculator to examine the values in the list associated with that Plot and to set some seemingly appropriate WINDOW values for that data. Then calculator displays the resulting Histogram.
Figure 19	Figure 19 shows the histogram with the class width and lower class limit that the calculator set. To see these values we move to the WINDOW screen by pressing .
Figure 20	These are the values that the calculator determined. We can change these and then display a new histogram.
Figure 21	We set Xmin to be the desired lower limit for the first class, in our case that would be 330. We set Xscl to 50 to make the class width 50. Because we want to include all of the data we set the Xmax value to be what would be the lower limit of the next class above our highest data value. [Note that frow our earlier work we know that highest value is 728, a value that we cannot determine from the original WINDOW settings.] Press to generate a new graph based on these new settings.
Figure 22	The histogram shown in Figure 22 corresponds to the frequencies that we found earlier by examining all of the sorted data. If we had not done that examination we could still have produced this histogram. In that case, we would want to use the histogram to get the values. We can do this by moving into "trace" mode by pressing which will move us to Figure 23.
Figure 23	In "trace" mode the calculator highlights the first column and displays the information that the column represents values from 330 up to but not including 380 and that there were 6 values in this class. We press to move to the next class.
Figure 24	From this display we see that the second class has 4 items in it.
Figure 25	Moving to the third class we see that it has 14 items. We could continue to move across the chart to determine the frequency in each class. From this we could build the table that we constructed before Figure 14.

Figure 26	We press to open the list of programs. In that list we move to the COLLATE3 program and press to select it.
Figure 27	That action pastes the command prgmCOLLATE3 onto the main screen. We press to have the calculator start the program.
Figure 28	The program starts and asks us for the location of the input data. Ours is in L1 so we press . Then we press to have the program continue.
Figure 29	The program tells us the lowest value in the list, 333, and the highest value in the list, 728. The program suggests a lower limit value for the first class, but we do not need to use that suggestion. In fact, we know that we want to use 330 as the first lower limit. We enter that value.
Figure 30	The program then suggests a class width to use, but we can make our own choice, which in this case we set to be 50.
Figure 31	The progam reports that it found 88 values and has put them into 8 classes. It then gives us some additional information. The calculator is in a "pause" condition so that we can read the information. We press to continue the program.
Figure 32	The progam concludes after showing us more information. Behind the scenes COLLATE3 has created some additional lists and it has reset the Stat Editor to display these lists. We move to the Stat Editor to see these values.
Figure 33	The first column, Low, gives the lowerr limit of each class. The second column, ICNT, gives the frequency of items in each class. These are the same values we found earlier. The third column, RFREQ, gives the relative frequency for each class.
Figure 34	Here we have moved down the lists to see the final class values. We do note that the first class has one extra entry. That is there to show the lower limit of the next class if it were there. We use that as the upper limit of the previous class.