For both correlation and regression we assume that we are dealing with
data that is given as pairs of values, an X value and a corresponding
Y value. The table below identifies such pairs of data, and it gives an
index value to each pair. With the assigned index value we can talk about the fifth pair and see that the
fifth pair is X=29 and Y=50. The following table gives the
pairs of values that we will use for this page.
Figure 1
|
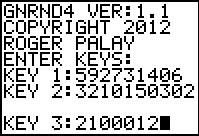
We start the GNRND4 program and use the key values shown in Figure 1.
One thing to note here is that based on the values in the
first key, the program determines that it requires two additional key
values. This difference is continued in Figure 2 where the
displayed output consistes of not one but two lists.
|
Figure 2
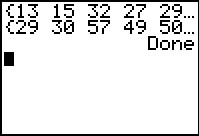 |
GNRND4 displays the first list and pauses to allow the user to scroll
across the items of that list. The user
presses  to signal the calculator to signal the calculator
|
to continue running the program.
GNRND4 then displays the second list and pauses to
allow the suer to scroll across those values.
These two lists correspond to the list of X and Y values
given in the table above.The first list is stored in
L1 while the second list is stored
in L2.
Figure 3
 |
We can plot these pairs of values. We use a coordinate axes system
to do this. On the calculator this is called a scatter plot.
We press  to open the STAT PLOT menu.
For the calculator used to generate these images the STAT PLOT
menu shows that Plot1 is On but it is set for a histogram, to open the STAT PLOT menu.
For the calculator used to generate these images the STAT PLOT
menu shows that Plot1 is On but it is set for a histogram,
 . We need to
change this. Press . We need to
change this. Press  to open the
Plot1 settings in Figure 4. to open the
Plot1 settings in Figure 4.
|
Figure 4
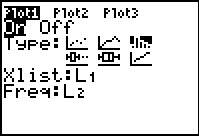 |
Here is the Plot1 screen before we have changed it.
We will move the highlight to the scatter plot icon,
 . Then we press . Then we press
 to change that to to change that to
 . .
|
Figure 5
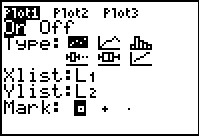 |
Figure 5 shows the changed settings. We note that we did not have to changes the
Xlist: setting because our X values are in L1.
Likewise, we did not have to changes the
Ylist: setting because our Y values are in L2.
Now that Plot1 is set, we move to set up the
window for the plot.
|
Figure 6
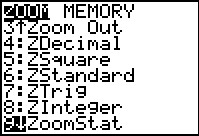 |
Press  to open the ZOOM menu and then
use the to open the ZOOM menu and then
use the  key to move down the the
9th item, ZoomStat.
When we select this item, by pressing the key to move down the the
9th item, ZoomStat.
When we select this item, by pressing the
 key,
the calculator will look at the data needed to complete the selected plot.
In our current case that will be the values in
L1 and L2.
Then, based on that data, the calculator will determine what it computes to
be the best values for the various WINDOW settings.
Having done that, the calculator moves directly to make and show the plot. key,
the calculator will look at the data needed to complete the selected plot.
In our current case that will be the values in
L1 and L2.
Then, based on that data, the calculator will determine what it computes to
be the best values for the various WINDOW settings.
Having done that, the calculator moves directly to make and show the plot.
|
Figure 7
 |
Here is a plot of the X,Y pairs of values. In this
case these pairs of values have a strong linear relation.
We can see this because the plotted points seem to fall
on a straight line. The two questions before us are
- What is the equation of the
line that "best" fits this data?
- The equation that we find will be the "best" fit, but just how good is that "fit"?
The command that will give us all of that information is
LinReg(ax+b). However, before we move to that command, we may want to take a slight detour.
|
Figure 8
 |
Looking ahead, we want to be sure that the calculator being used here
has Diagnostics turned ON. Once this has been turned ON
for a particualr calculator, it is supposede to stay ON. Therefore, this
should be a task that only needs to be done once. Still, it is nice to know how to do it
just in case it needs to be done again. If you are sure that your calculator has Diagnostics
turned On, then skip to Figure 11. Otherwise follow the steps here.
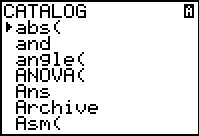
We find the command DiagnosticOn in the CATALOG.
We open the CATALOG by pressing
  .
Figure 8 shows the start of the CATALOG.
The CATALOG lists, in alphabetic order,
all of the commands that are available on the calculator.
We generally find most of those commands in the various menus.
DiagnosticOn is not in a menu. Therefore we need to look for it here
in the CATALOG. .
Figure 8 shows the start of the CATALOG.
The CATALOG lists, in alphabetic order,
all of the commands that are available on the calculator.
We generally find most of those commands in the various menus.
DiagnosticOn is not in a menu. Therefore we need to look for it here
in the CATALOG.
|
Figure 9
 |
We can scroll down to the command. There is a slight help in doing this.
If we press  , the key tied to the alphabetic character D,
then the calculator will jump down to the start of the D entries in
the CATALOG. That saves us some scrolling, though we still need to scroll down to the
desired command, as shown in Figure 9. , the key tied to the alphabetic character D,
then the calculator will jump down to the start of the D entries in
the CATALOG. That saves us some scrolling, though we still need to scroll down to the
desired command, as shown in Figure 9.
Once the command is highlighted, press
 to paste the command onto the main screen. to paste the command onto the main screen.
|
Figure 10
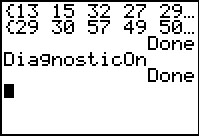 |
Once the command is pasted to the main screen
we press  to have the calculator perform the command.
It responds with Done when it is finished. to have the calculator perform the command.
It responds with Done when it is finished.
|
Figure 11
 |
Use  to open the STAT menu.
Use to open the STAT menu.
Use  to move to the CALC sub-menu.
Use to move to the CALC sub-menu.
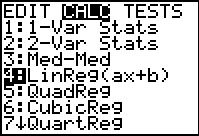
Use  to move the highlight down to
4:LinReg(ax+b), as shown in Figure 11. to move the highlight down to
4:LinReg(ax+b), as shown in Figure 11.
Press  to select that highlighted option
and paste it to the main screen. to select that highlighted option
and paste it to the main screen.
|
Figure 12
 |
We now have the right command in place. Given in this fashion,
the LinReg(ax+b) command will cause the calculator to compute,
from the data in L1 and
L2, the coefficient (a)
and the constant (b) in the
y =ax+b form of the linear equaton that
best fits the data in those lists.
We press  to have the calculator perform the command. to have the calculator perform the command.
|
Figure 13
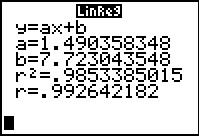 |
The result is shown in Figure 13. Here the calculator reminds us that the
form of the linear regression equation is y=ax+b. Then the
calculator tells us that the line of best fit will have
a=1.490358348 and b=7.723043548.
If we were to round these two values to the nearest hundredth, then
the linear regression equation could be written as
y = 1.49*x + 7.72
Furthermore, the calculator tells us that the correlation coefficient
for this data is r=.992642182. This is an extraordinarily high
correlation coefficient.
Correlation coefficients range from +1 to –1,
with high degrees correlation (i.e., having the plotted points be really close to a straight line)
being close to +1 and –1.
Situations where the plotted points are more spread out, not falling so close to a line,
have correlation coefficients
closer to zero. We will see this situation on a different web page.
|
Figure 14
 |
The first task is to get the calculator to draw
the linear regression equation.
To do this we open the Y= window via
 . The calcualtor is ready for us to type in the right side
of the linear regression equation. We might have written it down
from Figure 13. We might want to roundoff the coefficient and constant,
as we did in the discussion above, or we might want to use the full ten significant
digit version that the calculator gave us. Rounding means less typing.
There is some question as to where to round,
how many digits should we use? If we were toround to the nearest hundredth, then we could enter the
equaion here as 1.49*X+7.72, but we are not going to do that.
The calculator actually makes it easier to use the equation
that it determined rather than to use any rounded version.
The calculator can paste the equation that it determined directly into this
screen. We just have to find where the calcualtor stored the equation. . The calcualtor is ready for us to type in the right side
of the linear regression equation. We might have written it down
from Figure 13. We might want to roundoff the coefficient and constant,
as we did in the discussion above, or we might want to use the full ten significant
digit version that the calculator gave us. Rounding means less typing.
There is some question as to where to round,
how many digits should we use? If we were toround to the nearest hundredth, then we could enter the
equaion here as 1.49*X+7.72, but we are not going to do that.
The calculator actually makes it easier to use the equation
that it determined rather than to use any rounded version.
The calculator can paste the equation that it determined directly into this
screen. We just have to find where the calcualtor stored the equation.
|
Figure 15
 |
We use  to open the VARS menu. Then
we
highlight the fifth item, Statistics... and press to open the VARS menu. Then
we
highlight the fifth item, Statistics... and press  . .
|
Figure 16
 |
THis takes us to the VARS Statistics sub-menu. Here we have
all sorts of statistics variables that we can recall. However,
we want an equation. TO get that we move to the right
two times to get tot eh EQ, or equation, sub-menu.
|
Figure 17
 |
The first item in this sub-menu is RegEQ, our regression equation.
We press  to
select it and to paste it back into our Y= screen. to
select it and to paste it back into our Y= screen.
|
Figure 18
 |
Here we see that the calculator has pasted the entire original regression equation
onto this screen. A closer examination of that equation shows that the calculator actually pasted a
14-digit version of the equation here, not the shorter 10-digit values given in Figure 13.
Once the equation is here we can press  to return to the graph.
to return to the graph.
|
Figure 19
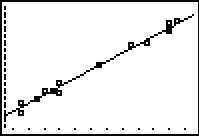 |
Now, in addition to the plotted points we have the graph of the linear regression line.
|
Figure 20
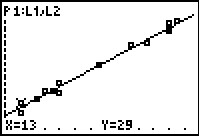 |
For Figure 20 we have moved into TRACE mode by pressing
the  key. The calculator starts by "tracing"
the plotted points. Note the P1:L1,L2 at the top of the screen. This indicates that
the calcualtor is ploting points from Plot1 and that Plot1 is based
on L1 and L2. key. The calculator starts by "tracing"
the plotted points. Note the P1:L1,L2 at the top of the screen. This indicates that
the calcualtor is ploting points from Plot1 and that Plot1 is based
on L1 and L2.
At the bottom of the screen the X=13 and Y=29 indicate
the coordinates of the highlighted point.
The highlighted point is a bit hard to see here, but it is the point
below the arrow in  . .
|
Figure 21
 |
Pressing the  key
takes the trace to the second point
in the data. This point is close to the first on the plot, but that is just an accident fo the
values in the original list. key
takes the trace to the second point
in the data. This point is close to the first on the plot, but that is just an accident fo the
values in the original list.
|
Figure 22
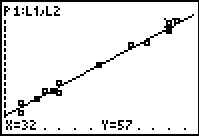 |
Pressing the  key
takes the trace to the third point
in the data.
Now we are at the upper right corner of the screen. key
takes the trace to the third point
in the data.
Now we are at the upper right corner of the screen.
|
Figure 23
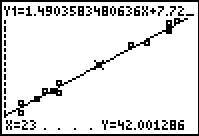 |
Pressing the  key takes us from
tracing the plotted points to tracing the graph of the equation.
Note that the equation being traced is now displayed across the top of the screen.
The calculator starts the trace half way across the screen.
The bottom of the screen displays the coordinates of the point being highlighted.
Somewhat as an accident and somewhat as just poor planning, the
highlight on the line is alos on one of the plotted points. key takes us from
tracing the plotted points to tracing the graph of the equation.
Note that the equation being traced is now displayed across the top of the screen.
The calculator starts the trace half way across the screen.
The bottom of the screen displays the coordinates of the point being highlighted.
Somewhat as an accident and somewhat as just poor planning, the
highlight on the line is alos on one of the plotted points.
|
Figure 24
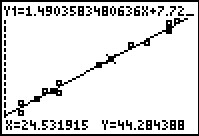 |
Now, because we are tracing the graph of the line, when we
press the  key the highlight just moves
a little bit to the right along the line. We will have to press the key the highlight just moves
a little bit to the right along the line. We will have to press the
 key six times to get to the display
in Figure 24. As we move, left or right, the screen updates to show us the X
and Y coordinates of the highlighted point. The Y values are the
expected value for each of the corresponding X values. key six times to get to the display
in Figure 24. As we move, left or right, the screen updates to show us the X
and Y coordinates of the highlighted point. The Y values are the
expected value for each of the corresponding X values.
We could use this feature to find expected values, but it is a pain to keep moving left and right in
such small increments. Also, the choice of X
values is a calculator decision. Thus, we can get close to an X value of
24 but we are not going to be right at 24 by moving the highlight left and right
like this.
|
Figure 25
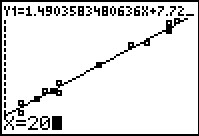 |
However, when we re in TRACE mode, as we are in Figure 24, we can just type in the
desired value of X. Figure 25 is the result o
pressing   .
We will be asking the calcualtor to jump to the point on the line that has an X
coordinate of 20. To get the calculator to do this we press .
We will be asking the calcualtor to jump to the point on the line that has an X
coordinate of 20. To get the calculator to do this we press
 . .
|
Figure 26
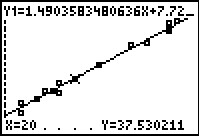 |
Now the trace is at the point X=20 and Y=37.530211, the
expected value. We might recall that when we used the rounded
linear regression equation our exected value, when X=20
was 37.52. The difference is that the graph here is using all 14 significant digits
of the equation and that causes a different, and more accurate, result.
|
Figure 27
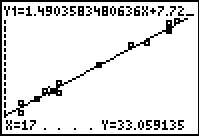 |
For Figure 27 we have moved the highlight directly to the
X value 17 by pressing
 . Now we see that the associated expected
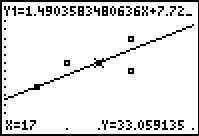
value is 33.059135. We know from the original table that for X=17 the
observed value is 33. This makes the associated residual
value 33-33.059135 = –0.059135. . Now we see that the associated expected
value is 33.059135. We know from the original table that for X=17 the
observed value is 33. This makes the associated residual
value 33-33.059135 = –0.059135.
|
Figure 28
 |
We can get a closer look at the data points and the line by changing the
WINDOW settigns. We move to the WINDOW menu via
 . Figure 28 shows the settings as determined
by the calculator back in Figure 6 when we used the ZoomStat command. . Figure 28 shows the settings as determined
by the calculator back in Figure 6 when we used the ZoomStat command.
|
Figure 29
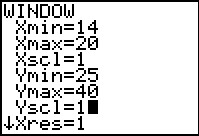 |
Figure 29 shows the modified WINDOW settings.
Here we 'have decided to only display X values
from 14 to 20 with an Xscl=1. The Y values range from
25 to 40.
Once these values are set we can return to the graph via
 . .
|
Figure 30
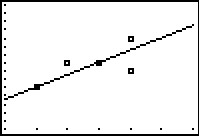 |
The new graph shows only the newly defined area.
|
Figure 31
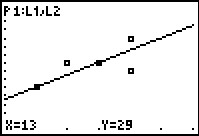 |
We reenter TRACE mode via  .
The top and bottom of the screen clearly show that we are
back in TRACE mode, but our highlighted point,
identified at the bottom as X=13 and Y=29 is not
highlighted on the screen.
This should be expected since we set the X values to range from 14 to 20,
leaving X=13 off the screen. .
The top and bottom of the screen clearly show that we are
back in TRACE mode, but our highlighted point,
identified at the bottom as X=13 and Y=29 is not
highlighted on the screen.
This should be expected since we set the X values to range from 14 to 20,
leaving X=13 off the screen.
|
Figure 32
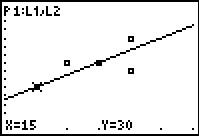 |
Still, we can use the  key to
move to another point of the data set. As it turns out, the next point,
X=15 and Y=30, is indeed on the screen. key to
move to another point of the data set. As it turns out, the next point,
X=15 and Y=30, is indeed on the screen.
|
Figure 33
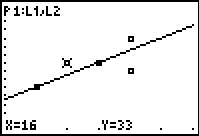 |
We can continue to look at the points on our plot. In Figure 33
we have moved to the thirteenth point of the plot,
X=16 and Y=33.
|
Figure 34
 |
We want to find the residual value at X=16. Therefore, we need to
find the value of the linear regression equation when
X=16. We use  to move from
tracing the plotted points to tracing the graph of the equation.
The calculator decides to put this trace at X=17. to move from
tracing the plotted points to tracing the graph of the equation.
The calculator decides to put this trace at X=17.
|
Figure 35
 |
We prepare to move to X=16
by typing   .
Then we can get the calcualtor to actually move thre by
pressing .
Then we can get the calcualtor to actually move thre by
pressing  to take us to Figure 36. to take us to Figure 36.
|
Figure 36
 |
Here the highlight is at X=16 and Y=31.56877.
This gives us the expected value. The residual
value is the (observed) – (expected), or in this case,
33-31.56877 = 1.43123.
|
Figure 37
 |
Earlier, in Figures 28 and 29, we brought the focus of the screen into a smaller
region than the original settings of the calculator. We can do the same thing, but in a slightly
diifferent fashion. To get to Figure 37 we press
 and then and then  .
THis highlights the Zoom In option. Then press .
THis highlights the Zoom In option. Then press
 to move to Figure 38. to move to Figure 38.
|
Figure 38
 |
The calculator has a flashing plus sign at the same place where we left the cursor in Figure 36.
One might note that we are no longer in TRACE mode here. We can tell
that because there is no tracing information at the top of the screen.
We can move the flashing plus sign anywhere we want on the screen to pick out
the center of our new screen. Once in place, we press  and the calculator will "zoom in", adjusting the WINDOW settings
so that the selected point in in the center of a new screen and the limits of the
new screen will be closer together than they are for the current screen.
and the calculator will "zoom in", adjusting the WINDOW settings
so that the selected point in in the center of a new screen and the limits of the
new screen will be closer together than they are for the current screen.
|
Figure 39
 |
Here is the new screen. We have narrowed the view to where we see only the one data point.
|
Figure 40
 |
Use  to return to TRACE mode.
Again, the calculator tries to trace the first data point,
but it is way off of this screen. to return to TRACE mode.
Again, the calculator tries to trace the first data point,
but it is way off of this screen.
|
Figure 41
 |
We press  to shift the TRACE to the
line. to shift the TRACE to the
line.
|
Figure 42
 |
We press  
 to force the calculator to move the the point on the
line where X=16. This shows the same expected
value that we had before. We do not get a better value by zooming in on the region. to force the calculator to move the the point on the
line where X=16. This shows the same expected
value that we had before. We do not get a better value by zooming in on the region.
|
Figure 43
 |
Residual values are so important that the calculator calculates them whenever it does a
LinReg(ax+b) command. There is one residual value generated for each
of the paired X and Y values. The calcualtor puts these values into a new list
that is named RESID. We can find that list by opening the
LIST menu, via   . .
|
Figure 44
 |
Then we need to sue the  key to move down the list
until we find the desired RESID name. key to move down the list
until we find the desired RESID name.
|
Figure 45
 |
We press  to select and paste that name onto the main screen.
Then we press to select and paste that name onto the main screen.
Then we press  again to perform that command. again to perform that command.
|
Figure 46
 |
The result is that the items in the list RESID are displayed.
Unfortunately, each item is so long that we really only get to see
the first item, in this case 1.90229727. We can use the
 key to scroll over to the right
to display more of the elements in the list named RESID. key to scroll over to the right
to display more of the elements in the list named RESID.
|
Figure 47
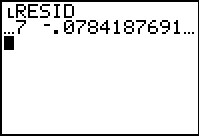 |
Figure 47 shows the start of the second number in RESID.
Clearly, this is an inefficient way to look at the residual values.
|
Figure 48
 |
As an alternative we could go back
and once again paste the RESID name onto the screen, but then follow it
with    as a command to take the values in RESID and copy them to the list
L3. At first this does not seem any better because the
calculator redisplays the list for us. However,
we recall that the StatEditor shows the contents of
L1, L2,
and L3.
as a command to take the values in RESID and copy them to the list
L3. At first this does not seem any better because the
calculator redisplays the list for us. However,
we recall that the StatEditor shows the contents of
L1, L2,
and L3.
|
Figure 49
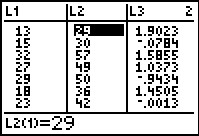 |
Press   to get to Figure 49. Here we can see the X values in
L1, the Y values in
L2, and now the residual
values in L3.
to get to Figure 49. Here we can see the X values in
L1, the Y values in
L2, and now the residual
values in L3.
|
Figure 50
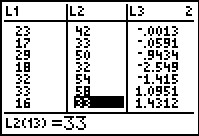 |
If we want to know the residual value associated with the
thirteenth data pair, X=16 and Y=33, then we can move
down the list to the 13th row
and see that the residual value is 1.4312.
We could safely exit the StatEditor via the 
 sequence. sequence.
|
Figure 51
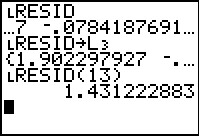 |
Back in the main screen, we see yet another way to look at the residual
values. Again, this uses the list of residual values named RESID.
We can get a display of any one of the values in that list
by pasting the name of the list onto the
main screen and tehn following it with the desired index value enclosed in
parentheses. Thus the command RESID(13) displays the value in the
thirteenth item of the list.
|


 to signal the calculator
to signal the calculator

 to open the STAT PLOT menu.
For the calculator used to generate these images the STAT PLOT
menu shows that Plot1 is On but it is set for a histogram,
to open the STAT PLOT menu.
For the calculator used to generate these images the STAT PLOT
menu shows that Plot1 is On but it is set for a histogram,
 . We need to
change this. Press
. We need to
change this. Press  to open the
Plot1 settings in Figure 4.
to open the
Plot1 settings in Figure 4.

 . Then we press
. Then we press
 to change that to
to change that to
 .
.


 to open the ZOOM menu and then
use the
to open the ZOOM menu and then
use the  key to move down the the
9th item, ZoomStat.
When we select this item, by pressing the
key to move down the the
9th item, ZoomStat.
When we select this item, by pressing the
 key,
the calculator will look at the data needed to complete the selected plot.
In our current case that will be the values in
L1 and L2.
Then, based on that data, the calculator will determine what it computes to
be the best values for the various WINDOW settings.
Having done that, the calculator moves directly to make and show the plot.
key,
the calculator will look at the data needed to complete the selected plot.
In our current case that will be the values in
L1 and L2.
Then, based on that data, the calculator will determine what it computes to
be the best values for the various WINDOW settings.
Having done that, the calculator moves directly to make and show the plot.



 .
Figure 8 shows the start of the CATALOG.
The CATALOG lists, in alphabetic order,
all of the commands that are available on the calculator.
We generally find most of those commands in the various menus.
DiagnosticOn is not in a menu. Therefore we need to look for it here
in the CATALOG.
.
Figure 8 shows the start of the CATALOG.
The CATALOG lists, in alphabetic order,
all of the commands that are available on the calculator.
We generally find most of those commands in the various menus.
DiagnosticOn is not in a menu. Therefore we need to look for it here
in the CATALOG.

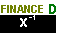 , the key tied to the alphabetic character D,
then the calculator will jump down to the start of the D entries in
the CATALOG. That saves us some scrolling, though we still need to scroll down to the
desired command, as shown in Figure 9.
, the key tied to the alphabetic character D,
then the calculator will jump down to the start of the D entries in
the CATALOG. That saves us some scrolling, though we still need to scroll down to the
desired command, as shown in Figure 9.
 to paste the command onto the main screen.
to paste the command onto the main screen.

 to have the calculator perform the command.
It responds with Done when it is finished.
to have the calculator perform the command.
It responds with Done when it is finished.

 to open the STAT menu.
Use
to open the STAT menu.
Use  to move to the CALC sub-menu.
Use
to move to the CALC sub-menu.
Use  to move the highlight down to
4:LinReg(ax+b), as shown in Figure 11.
to move the highlight down to
4:LinReg(ax+b), as shown in Figure 11.
 to select that highlighted option
and paste it to the main screen.
to select that highlighted option
and paste it to the main screen.

 to have the calculator perform the command.
to have the calculator perform the command.



 to open the VARS menu. Then
we
highlight the fifth item, Statistics... and press
to open the VARS menu. Then
we
highlight the fifth item, Statistics... and press 


 to return to the graph.
to return to the graph.


 key. The calculator starts by "tracing"
the plotted points. Note the P1:L1,L2 at the top of the screen. This indicates that
the calcualtor is ploting points from Plot1 and that Plot1 is based
on L1 and L2.
key. The calculator starts by "tracing"
the plotted points. Note the P1:L1,L2 at the top of the screen. This indicates that
the calcualtor is ploting points from Plot1 and that Plot1 is based
on L1 and L2.
 .
.



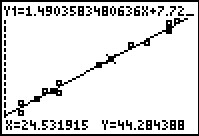


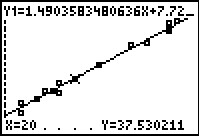
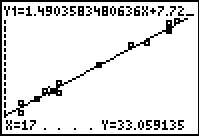









 .
Then we can get the calcualtor to actually move thre by
pressing
.
Then we can get the calcualtor to actually move thre by
pressing 













 as a command to take the values in RESID and copy them to the list
L3. At first this does not seem any better because the
calculator redisplays the list for us. However,
we recall that the StatEditor shows the contents of
L1, L2,
and L3.
as a command to take the values in RESID and copy them to the list
L3. At first this does not seem any better because the
calculator redisplays the list for us. However,
we recall that the StatEditor shows the contents of
L1, L2,
and L3.


 sequence.
sequence.
