This page is devoted to presenting, in a
step by step fashion, the keystrokes and the
screen images for obtaining values for a
Binomial Distribution on a TI-83 (TI-83 Plus, or TI-84 Plus)
calculator.
Figure 1
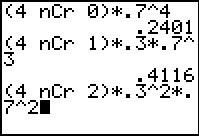
| The case we will examine here is to have `n` trials with a
probability of success `p=0.3`.
Using the equation `P(x) = quad_nC_xp^x(1-p)^(n-x)` we could realy
compute the probabilty of 0 successes.
The equation becomes `P(0) = quad_4C_0*.7^4`. We construct that on the main
screen, shown in Figure 1.
In that Figure we also see the value of `P(0)=.2401`,
the expression for `P(1) = quad_4C_1*.3*.7^3`, the value of `P(1)=.4116`
and the expression for `P(2) = quad_4C_2*.3^2*.7^2`.
|
Figure 1a
 |
We continue in Figure 1a with the value of `P(2)=.2646`, the
expression for `P(3) = quad_4C_3*.3^3*.7^1`,
and the value of `P(3)=.0756`.
|
Figure 1b
 |
We conclude all the possible results from `4` trials with the
expression for `P(4) = quad_4C_4*.3^4` and the value of `P(4)=.0081`.
Seeing that we can do this is nice, but it would be so much more convenient for
the calculator to help us on this. To that end the calculator
is designed to give us
certain probability distributions, one of which is the
binomial distribution.
|
Figure 1c
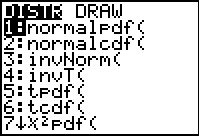 |
To get to the image in Figure 1c we press
  .
This takes us to the DIST (distribution) menu.
The operation that we want, binompdf(, is not shown here.
We need to move down the menu to find it. .
This takes us to the DIST (distribution) menu.
The operation that we want, binompdf(, is not shown here.
We need to move down the menu to find it.The pdf
in binompdf( stands for probability
distribution function.
|
Figure 2
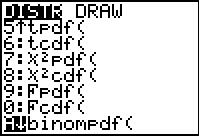 |
In FIgue 2 we have moved down the menu to
locate and highlight binompdf(.
We perss  to select and paste that item. to select and paste that item.
|
Figure 3
 |
Figure 3 shows the pasted text binompdf(.
That command will compute the binomial probability
for a case where, for we have a given number of trials and
a given probability
of success, we want the probability of a specific number of successes.
To do this we need to tell the calculator all three of those values:
- number of trials
- probability of a success on a single trial
- specific number of successes for which we want this computed
Our problem is to remember the
sequence in whch we are to supply these values.
|
Figure 4
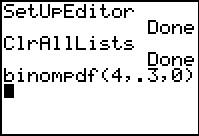 |
The binompdf( command wants the values in
exactly the order that we have listed them above.
In Figure 4 we have asked for the binomial
distribution probability
that in 4 trials with a probability of
a single success being 0.3
we find 0 successes.
Press  to have the
calculator perform the command. to have the
calculator perform the command.
|
Figure 5
 |
The result, shown in Figure 5, is .2401, exactly what we
computed in Figure 1.
We have gone further in Figure 5 by recalling the previous
command via   and then using the cursor keys to move back to the command and
to change the specification of the desired number of successes to 1.
Again, we perform the command via
and then using the cursor keys to move back to the command and
to change the specification of the desired number of successes to 1.
Again, we perform the command via
 and move to Figure 6 and move to Figure 6
|
Figure 6
 |
Here we see that the `P(1)=.4116`, that we have again recalled the command,
modified it to ask for the probability of exactly 2 successes,
and found that `P(2)=.2646`.
|
Figure 7
 |
In Figure 7 we complete the study
by finding the two remaining probabilities.
The values have not changed from our earlier calcualtions
but the process is a bit easier.
|
Figure 8
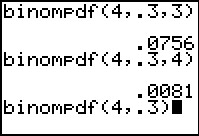 |
The binompdf( command has one other useful feature, namely,
if we omit the final field then the command computes
the probabilities for each of the possible
values for that field putting the answer in the form of a list of
values. At the bottom of Figure 8 we have formed and
performed the command binompdf(4,.3).
|
Figure 9
 |
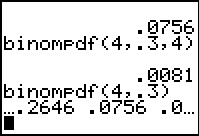
We perform the command via  .
The calcualtor displays the first portion of the answer, the list of values
for P(0), P(1), and the start of P(2). .
The calcualtor displays the first portion of the answer, the list of values
for P(0), P(1), and the start of P(2).
|
Figure 10
 |
We can scroll across this to see more of the values.
|
Figure 11
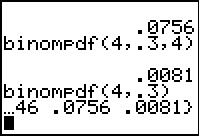 |
In Figure 11 we have finished scrolling and we now see
the last of the values.
|
Figure 12
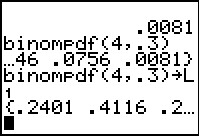 |
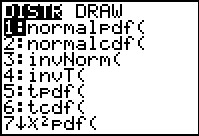
Because the binompdf(4,.3) command produces a
list we can assign that list to
a list in the calculator. For Figure 12 we have recalled
the command and appended the 
  action.
Then we performed the command via action.
Then we performed the command via .
The result seems to be the same as before, namely a display
of the computed values. .
The result seems to be the same as before, namely a display
of the computed values.
|
Figure 13
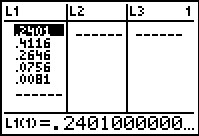 |
However, if we move to the StatEditor
we see the entire list of values has been stored in L1.
One major word of caution here. Note that index 1
of the list, that is L1(1)
holds the value for P(0), not P(1).
To find P(1) we need to look at index 2, namely,
L1(2).
Now that we have the values in L1
it would be easy for us to create the cumulative sum of
those values in L2. We could just move to the LIST
menu, then to the OPS sub-menu, select the cumsum( option
and formulate and execute the command cumsum(L1) L2. L2.
|
Figure 14
 |
Rather than do that, the calculator provides another command,
binomcdf(, that computes the cumulative probability distribution
for specified values. In fact, the values are in the
same order as we hade in the earlier binompdf( command. The
only difference is that for the binomcdf( command the interpretation of the result is
changed giving the sum of the probabilities of having the number of successes in
n trials with 0 up to and including
the specified number of successes. We use   to return to the DIST menu. Then we move down th menu to find binomcdf(.
to return to the DIST menu. Then we move down th menu to find binomcdf(.
|
Figure 15
 |
Having found and highlighted the option, press to paste it onto the main screen.
to paste it onto the main screen.
|
Figure 16
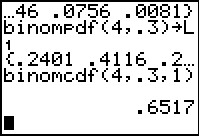 |
In Figure 16 we have completed the command by indicating that we are
looking at 4 trials where the probability of a single
success is 0.3, and we want the probability that the number of successes
in those four trials is less than or equal to 1.
The result, .6517 is just what we would expect since we know,
from Figure 13 that we expect the anser to be the sum .2401+.4116.
|
Figure 17
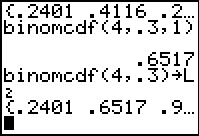 |
binomcdf( works the way binompdf( did in that if we omit the
final value then the result is a list of values,
one for each of the possible number of successes. In Figure 17 we
have made such a command and put the result into L2.
The start of the resulting list is shown on the screen.
|
Figure 18
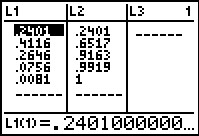 |
We return to the StatEditor and we see the new values in
L2. We could use these to solve a number of
different kinds of problems, but why use the table when the binompdf(
and
binomcdf( commands recompute the values any time we want them?
|
Binomial distribution probabilities lend themselves to just
six kinds of problems.
We will look at these, but we will pose them in the
setting of having 17 trials
with a 0.385 probability of success.
Here are the six types of questions, with specific values
for illustration:
Create the L1 and L2 lists
|
Figure 19
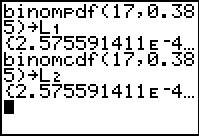 |
First we will generate the two lists, the proability valeus and the cumulative
probability values, in L1
and L2, respectively.
We note here that the P(0) is given as
2.575591411E–4,
meaning 2.575591411*10–4..
To express this number without the power of 10 we just need to move the
decimal point 4 places to the left to get 0.0002575591411.
|
Use the StatEditor to inspect the values in those lists.
|
Figure 20
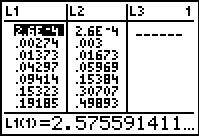 |
Then we move to the StatEditor to inspect those values.
Unfortunately, we can only see 7 values for each list at a time
in the editor.
Note that the value of L1(1),
which holds P(0) is given as 2.6E–4,
meaning 2.6**10–4. To express this without
using the power of 10 we just move the decimal
point four places to the left to get 0.00026.
We also note that the values in the table portion of the display have been rounded
to use only 5 characters (6 including the decimal point). We can still
see the full value for a specific item
by highlighting that item in the table.
It is also important to remember that the index for items in the
list corresponds to having one fewer than the index number of successes.
Thus, the seventh item in L1, namely
.19185, corresponds to P(6).
|
Figure 21
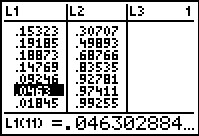 |
In Figure 21 we have moved down the list and then back up one iotem so that
the highlight is on L1(11) which
corresponds to P(10).
|
Figure 22
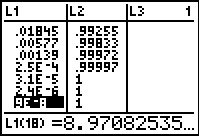 |
Moving down to the bottom of the list, the display is now
at L1(18) which corresponds to
P(17), showing a value there of 9E–8,
meaning 9*10–8 which
we would expand, by moving the decimal 8 places to the left, as
0.00000009. Of course, seeing the more accurate 8.97082535...
at the bottom of the screen, we realize that the 9 shown in
the table value 9E–8,
is just the rounded version of 8.97082535.... We have no
way on this screen to see the rest of
8.97082535.... Once we are back to the main screen we could
just type L1(18) to see the rest of this entry.
It would appear as 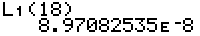 .
Thus, the more accurate expansion would be 0.0000000897082535,
not that we would ever need such accuracy in a real problem. .
Thus, the more accurate expansion would be 0.0000000897082535,
not that we would ever need such accuracy in a real problem.
|
Figure 23
 |
Q1:
To answer "What is the probability that we get exactly 10 successes?"
we just need to move back to see the
value in L1(11). Therefore, the
answer is 0.0463.
Q2:
To answer "What is the probability that we get 10 or fewer successes?
we read across to the value in
L2(11).
Therefore, the
answer is 0.97411.
Q3:
To answer "What is the probability of that we get 10 or more successes?"
we need to realize that the answer will be 1-P(x≤9), and that
the value of P(x≤9) is at
index 10 of L2.
Therefore, the
answer is 1 – 0.92781 or 0.07219.
|
Figure 24
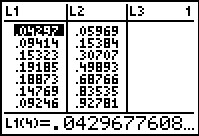 |
Q4:
To answer "What is the probability of getting
between 4 and 10 successes, inclusive of 4 and 10?"
we need to realize that the answer will be P(x≤10)-P(x≤3).
We saw above that P(x≤10) is 0.97411. We move back up the table
to find
the value of P(x≤3) is at
index 4 of L2,
namely, 0.05969.
Therefore, the
answer is 0.97411 – 0.05969 or 0.91442.
Q5:
To answer "What is the probabilty of getting 5, 8, or 11 successes?"
we need to realize that the answer will be the sum of
the probabilities or getting exactly 5, exactly 8, and exactly 11
successes. We have seen all of these in the various screens
in the L1 column.
The value of P(x=5) is at
index 6 of L1,
namely 0.15323.
The value of P(x=8) is at
index 9 of L1,
namely 0.14769.
The value of P(x=11) is at
index 12 of L1,
namely 0.01845 (see Figure 21).
Therefore, the
answer is 0.15323+0.14769+0.01845 or 0.31937.
Q6:
To answer "What is the probability of not getting 10 successes?"
we need to realize that the answer will be 1-P(x=10), and that
the value of P(x=9) is at
index 11 of L2.
Therefore, the
answer is 1 – 0.0463 or 0.9537.
(This is the same technique that we used in question type 3.
However, this is a more general statement. To get
the probability of not getting some value, or values,
take 1 minus the probability of
getting that value (or those values).
|
Use the direct reference to values in the lists.
|
Figure 25
 |
We will do all of the problems again, this time using direct references to
the values that we stored in L1 and
L2 back in Figure 19.
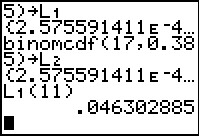
Q1:
To answer "What is the probability that we get exactly 10 successes?"
we want P(x=10) which is stored in
L1(11). The answer is
0.046302885.
|
Figure 26
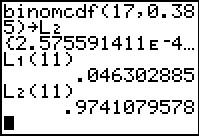 |
Q2:
To answer "What is the probability that we get 10 or fewer successes?"
we want P(x≤10) which is stored in
L2(11). The answer is
0.9741079578.
|
Figure 27
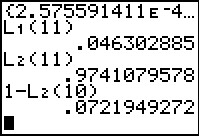 |
Q3:
To answer "What is the probability of that we get 10 or more successes?"
we need to realize that the answer will be 1-P(x≤9), and that
the value of P(x≤9) is at
index 10 of L2.
Therefore, we get the
answer from 1–L2(10)
which gives 0.0721949272.
|
Figure 28
 |
Q4:
To answer "What is the probability of getting
between 4 and 10 successes, inclusive of 4 and 10?"
we need to realize that the answer will be P(x≤10)-P(x≤3).
The value of P(x≤10) is
at L2(11).
The value of P(x≤3) is at
L2(4).
Therefore, we get the answer from
L2(11)–L2(4)
which gives 0.9144142597.
|
Figure 29
 |
Q5:
To answer "What is the probabilty of getting 5, 8, or 11 successes?"
we need to realize that the answer will be the sum of
the probabilities or getting exactly 5, exactly 8, and exactly 11
successes. We have all of these in
L1(6),
L1(9), and
L1(12), respectively.
Therefore, we get the answer from
L1(6)+L1(9)+L1(12)
which gives 0.31936849.
|
Figure 30
 |
Q6:
To answer "What is the probability of not getting 10 successes?"
we need to realize that the answer will be 1-P(x=10), and that
the value of P(x=9) is at
index 11 of L2.
Therefore, we get the answer
from 1–L1(11)
which gives 0.953697115.
(This is the same technique that we used in question type 3.
However, this is a more general statement. To get
the probability of not getting some value, or values,
take 1 minus the probability of
getting that value (or those values).
|
Just use binompdf( and binomcdf( directly.
|
Figure 31
 |
We will do all of the problems again, this time using direct references to
the binompdf( and binomcdf( commands. For thise we did not even
need to do the steps in Figure 19.
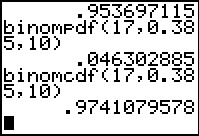
Q1:
To answer "What is the probability that we get exactly 10 successes?"
we want the binompdf(17,0.385,10) command. It produces
0.046302885.
|
Figure 32
 |
Q2:
To answer "What is the probability that we get 10 or fewer successes?"
we want the binomcdf(17,0.385,10) command. It produces
0.9741079578.
|
Figure 33
 |
Q3:
To answer "What is the probability of that we get 10 or more successes?"
we need to realize that the answer will be 1-P(x≤9).
The command
1- binomcdf(17,0.385,9)
produces 0.0721949272.
|
Figure 34
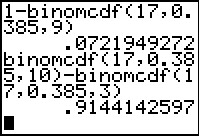 |
Q4:
To answer "What is the probability of getting
between 4 and 10 successes, inclusive of 4 and 10?"
we need to realize that the answer will be P(x≤10)-P(x≤3).
The command binomcdf(17,0.385,10)-binomcdf(17,0.385,3)
produces 0.9144142597.
|
Figure 35
 |
Q5:
To answer "What is the probabilty of getting 5, 8, or 11 successes?"
we need to realize that the answer will be the sum of
the probabilities or getting exactly 5, exactly 8, and exactly 11
successes. The command
binompdf(17,0.385,5)+binompdf(17,0.385,8)+binompdf(17,0.385,11)
produces 0.31936849.
|
Figure 36
 |
Q6:
To answer "What is the probability of not getting 10 successes?"
we need to realize that the answer will be 1-P(x=10).
The command 1-binompdf(17,0.385,10)
produces 0.953697115.
(This is the same technique that we used in question type 3.
However, this is a more general statement. To get
the probability of not getting some value, or values,
take 1 minus the probability of
getting that value (or those values).
|
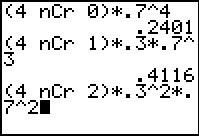




 .
This takes us to the DIST (distribution) menu.
The operation that we want, binompdf(, is not shown here.
We need to move down the menu to find it.
.
This takes us to the DIST (distribution) menu.
The operation that we want, binompdf(, is not shown here.
We need to move down the menu to find it.
 to select and paste that item.
to select and paste that item.


 to have the
calculator perform the command.
to have the
calculator perform the command.


 and then using the cursor keys to move back to the command and
to change the specification of the desired number of successes to 1.
Again, we perform the command via
and then using the cursor keys to move back to the command and
to change the specification of the desired number of successes to 1.
Again, we perform the command via
 and move to Figure 6
and move to Figure 6




 .
The calcualtor displays the first portion of the answer, the list of values
for P(0), P(1), and the start of P(2).
.
The calcualtor displays the first portion of the answer, the list of values
for P(0), P(1), and the start of P(2).





 action.
Then we performed the command via
action.
Then we performed the command via .
The result seems to be the same as before, namely a display
of the computed values.
.
The result seems to be the same as before, namely a display
of the computed values.

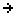 L2.
L2.


 to return to the DIST menu. Then we move down th menu to find binomcdf(.
to return to the DIST menu. Then we move down th menu to find binomcdf(.

 to paste it onto the main screen.
to paste it onto the main screen.







 .
Thus, the more accurate expansion would be 0.0000000897082535,
not that we would ever need such accuracy in a real problem.
.
Thus, the more accurate expansion would be 0.0000000897082535,
not that we would ever need such accuracy in a real problem.













