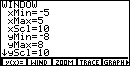The general graph of an Odd Degree Polynomial
The text uses the following graph, or one quite similar to it, as the graph of a
general odd degree polynomial with a positive leading coefficient.
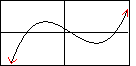 That particular graph was generated with a window setting of
That particular graph was generated with a window setting of
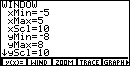 Unfortunately, the graph of the polynomial gives a number of erroneous
impressions. The only thing that we do know for sure is that the graph must go down to the
left and up to the right. We do not know what happens in the middle.
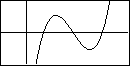
The image shown above implies that the graph crosses the x-axis in three places.
This is not necessarily so. It is true that the graph of an odd degree polynomial must
cross the x-axis in at least one place. But a general odd degree polynomial
may cross in many places, any number of which may be to the left or to the right of the origin.
We just do not know. The most we can say about the graph of
an odd degree polynomial with a leading positive coefficient is that it
will appear as
Unfortunately, the graph of the polynomial gives a number of erroneous
impressions. The only thing that we do know for sure is that the graph must go down to the
left and up to the right. We do not know what happens in the middle.
The image shown above implies that the graph crosses the x-axis in three places.
This is not necessarily so. It is true that the graph of an odd degree polynomial must
cross the x-axis in at least one place. But a general odd degree polynomial
may cross in many places, any number of which may be to the left or to the right of the origin.
We just do not know. The most we can say about the graph of
an odd degree polynomial with a leading positive coefficient is that it
will appear as
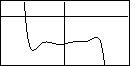
 where we do not know what happens inside the middle box and we do not know where the box is
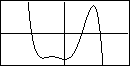
with respect to the coordinate axes. For example, each of the following is a graph of an
odd degree polynomial with a leading positive coefficient.
where we do not know what happens inside the middle box and we do not know where the box is
with respect to the coordinate axes. For example, each of the following is a graph of an
odd degree polynomial with a leading positive coefficient.
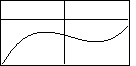
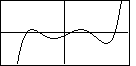
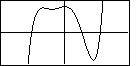
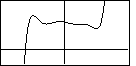
On the other hand, the text presents the graph of a general odd degree polynomial with
a negative leading coefficient as
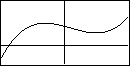
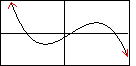 Again, this graph may give some wrong impressions. All that we
know for sure is that the graph must go up at the left and down at the right.
The general graph should be presented as
Again, this graph may give some wrong impressions. All that we
know for sure is that the graph must go up at the left and down at the right.
The general graph should be presented as
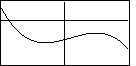
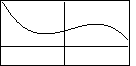
 where, again, we do not know what happens in side the middle box and we do not know where
that box is in relation to the coordinate axes.
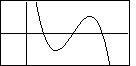
For example, each of the following is a graph of an
odd degree polynomial with a leading negative coefficient.
where, again, we do not know what happens in side the middle box and we do not know where
that box is in relation to the coordinate axes.
For example, each of the following is a graph of an
odd degree polynomial with a leading negative coefficient.

PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay