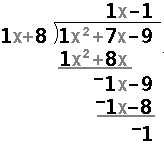
|

|
In order to show all of the work for the problem, the TI-89 uses a matrix to hold the divisor, the dividend, the quotient, the remainder, and all of the rest of the computations. For example consider the problem on the left, and its representation in polydiv on the right.
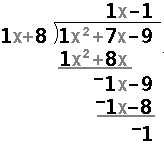
|

|
|
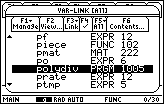
Figure 1 is the result of pressing
the   keys to
open the List of Variables. The TI-89 responds with a list of all variables.
We use the keys to
open the List of Variables. The TI-89 responds with a list of all variables.
We use the  key to move to successive variables that
start with the letter "P", remembering that the TI-89 is not case-sensitive.
We could also use the the key to move to successive variables that
start with the letter "P", remembering that the TI-89 is not case-sensitive.
We could also use the the  key
to move the highlight. In any case, Figure 1 demonstrates that we have
moved to highlight the polydiv name.
Once the polydiv program has been selected, we press the key
to move the highlight. In any case, Figure 1 demonstrates that we have
moved to highlight the polydiv name.
Once the polydiv program has been selected, we press the
 key to move to Figure 2. key to move to Figure 2.
|
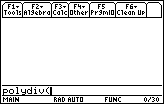
| The actions of Figure 1 have pasted the name of our program, polydiv, into the command line of the calculator. In addition, the calculator has appended the required left parenthesis. There are no parameters for the polydiv program. Therefore, we can complete the command by supplying the matching right parenthesis. |
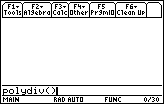
| In Figure 3 we have completed the command
by pressing the  key. key.
Now to begin the program we press the |
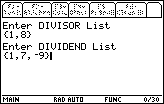
| The polydiv program prompts us for the DIVISOR LIST.
We respond by entering
 key to have the calculator accept our
list. Then the program moves on to prompt for the DIVIDEND LIST.
We respond with key to have the calculator accept our
list. Then the program moves on to prompt for the DIVIDEND LIST.
We respond with We press the |
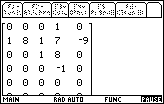
| The polydiv program displays the initial matrix in Figure 5.
At this point the initial division has been done. That is, the program
reflects the problem at the stage of completing the initial division, namely,
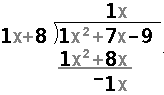  to continue
the division and move to Figure 6. to continue
the division and move to Figure 6.
|
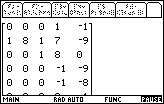
| In Figure 6 the program has taken another step, determining the
second coefficient in the quotient. In this case, that is really all that there is to the
problem. Again the program is in a paused state so that we can move around in the
matrix if need be.
And, indeed, we can not see the bottom row of the matrix.
Therefore, we press the
 key to shift the display to that of Figure 7. key to shift the display to that of Figure 7.
|
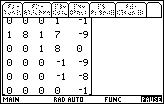
| Here we see the rest of the matrix.
Having seen all of the problem we press
 to continue, and move to Figure 8. to continue, and move to Figure 8.
|
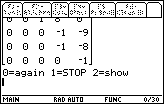
| Once the program has reached the end of the division,
the polydiv program displays
the menu shown in Figure 8. This allows us to
start a new problem by pressing 0 end the polydiv program by pressing 1 show the answer to the last problem by pressing 2. |
Let us look at another problem, namely,
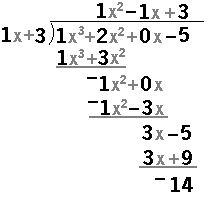
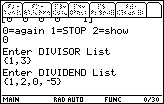
| We left Figure 8 by pressing the
 key to tell the calculator that we have a new problem to do.
The polydiv program again asks for the DIVISOR LIST, to
which we respond with key to tell the calculator that we have a new problem to do.
The polydiv program again asks for the DIVISOR LIST, to
which we respond with
 .
The program then asks for the DIVIDEND LIST.
Figure 9 shows that list as .
The program then asks for the DIVIDEND LIST.
Figure 9 shows that list as
|
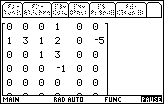
| Pressing  moves
the program from Figure 9 to Figure 10.
The program is paused. We can examine the output and note that the
first coefficient of the quotient is 1. Press moves
the program from Figure 9 to Figure 10.
The program is paused. We can examine the output and note that the
first coefficient of the quotient is 1. Press
 to move to Figure 11. to move to Figure 11.
|

| Figure 11 shows the calculator display after the second cycle
of the division algorithm. The second coefficient of the quotient
has been computed to be "– 1" and
the corresponding portion of the division algorithm has been completed.
Press
 to move to Figure 12. to move to Figure 12.
|

| Again, we can use the  key to move the display down to show the rest of the matrix, as it appears in
Figure 12.
key to move the display down to show the rest of the matrix, as it appears in
Figure 12.
Press
|

| Figure 13 shows the top portion of the final matrix.
Again, we can use the  key to move the display down to show the rest of the matrix, as it appears in
Figure 14.
key to move the display down to show the rest of the matrix, as it appears in
Figure 14.
|

| Here is the lower portion of the matrix. The problem is done. If we press the ENTER the program will display the options to do a new problem, quit, or re-display the current matrix. |
Here is one more example:
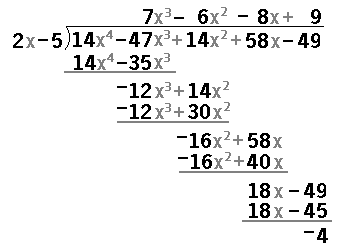
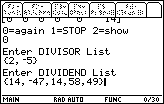
| In Figure 15 we have pressed  to ask for a new problem, and we have entered both
the DIVISOR LIST and the DIVIDEND LIST.
to ask for a new problem, and we have entered both
the DIVISOR LIST and the DIVIDEND LIST.
|

| Press  to move from Figure 15 to
Figure 16. Here we can see the matrix after the first step of the algorithm. to move from Figure 15 to
Figure 16. Here we can see the matrix after the first step of the algorithm.
|

| Press  to move from Figure 16 to
Figure 17. Here we can see the matrix after the second step of the algorithm. to move from Figure 16 to
Figure 17. Here we can see the matrix after the second step of the algorithm.
|

| Press  to move from Figure 17 to
Figure 18. Here we can see the matrix after the third step of the algorithm.
As in the earlier example, we can not see the bottom portion
of the matrix.
We press the to move from Figure 17 to
Figure 18. Here we can see the matrix after the third step of the algorithm.
As in the earlier example, we can not see the bottom portion
of the matrix.
We press the  key to move the
display down so that we can see the rest of the
matrix in Figure 19. key to move the
display down so that we can see the rest of the
matrix in Figure 19.
|

| In Figure 19 we can see the rest of the matrix. We press the
 key to continue the algorithm. key to continue the algorithm.
|

| Now we can see the matrix after the fourth and final step.
However, now we are missing both the bottom of the
matrix and the right side of the matrix.
We can use both the  key
and the key
and the  key to move down and to the
right to see the rest of the matrix, as shown in Figure 21. key to move down and to the
right to see the rest of the matrix, as shown in Figure 21.
|

| Figure 21 shows the rest of the matrix.
We can press the  key to return to
our menu. key to return to
our menu. |
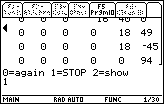
| In Figure 22 we see the conclusion of the
program. We have responded to the menu by pressing the
 key and
the key and
the  key.
The TI-89 remains in the Program IO screen that is Figure 21. We would have to press the key.
The TI-89 remains in the Program IO screen that is Figure 21. We would have to press the
 key to
return to the main screen. key to
return to the main screen. |
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay