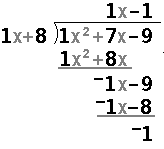
|

|
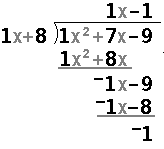
|

|

|
Figure 1 is the result of pressing
the  key to open the PROGRAM menu,
using the and then key to open the PROGRAM menu,
using the and then  key if need be to
shift the display to the point where the "polydi" option is visible, and then
using the appropriate key
to select the desired option. In the
case shown in Figure 1
we use the key if need be to
shift the display to the point where the "polydi" option is visible, and then
using the appropriate key
to select the desired option. In the
case shown in Figure 1
we use the  key to paste the name of the program onto the screen.
Once the polydiv program has been pasted onto the screen, we press the key to paste the name of the program onto the screen.
Once the polydiv program has been pasted onto the screen, we press the
 key to move to Figure 2. key to move to Figure 2.
|

| Figure 2 shows the program window after we havee responded to the
two prompts that the program gives us. First, the program asks us
for the DIVISOR VECTOR. We respond with
 key
to submit that response. The program
prompts us for the DIVIDEND VECTOR.
For our problem we respond with key
to submit that response. The program
prompts us for the DIVIDEND VECTOR.
For our problem we respond with
 key. key.
|
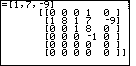
| The polydiv program displays the initial matrix in Figure 3.
At this point the initial division has been done. That is, the program
reflects the problem at the stage of completing the initial division, namely,
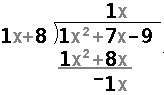  to continue
the division and move to Figure 4. to continue
the division and move to Figure 4.
|
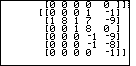
| In Figure 4 the program has taken another step, determining the
second coefficient in the quotient. In this case, that is really all that there is to the
problem. Again the program is in a paused state so that we can move around in the
matrix if need be.
For this problem we can see all of the answer on the screen.
Therefore, we do not need to look at any hidden values. We press
 to continue, and move to Figure 5. to continue, and move to Figure 5.
|
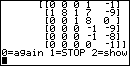
| Once the program has reached the end of the division, the polydiv
program displays
the menu shown in Figure 5. This allows us to
start a new problem by pressing 0 end the POLYDIV1 program by pressing 1 show the answer to the last problem by pressing 2. |
Let us look at another problem, namely,
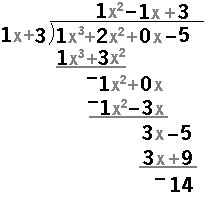

| We left Figure 5 by pressing the
 key to tell the calculator that we have a new problem to do.
The polydiv program again asks for the DIVISOR VECTOR, to
which we respond with key to tell the calculator that we have a new problem to do.
The polydiv program again asks for the DIVISOR VECTOR, to
which we respond with
 . The program then asks for the
DIVIDEND VECTOR.
Figure 6 shows that vector as . The program then asks for the
DIVIDEND VECTOR.
Figure 6 shows that vector as
|
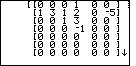
| Pressing  moves the program from Figure 6 to Figure 7.
The program is paused. We can examine the output and note that the
first coefficient of the quotient is 1. Press
moves the program from Figure 6 to Figure 7.
The program is paused. We can examine the output and note that the
first coefficient of the quotient is 1. Press
 to move to Figure 8. to move to Figure 8. |
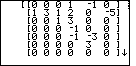
| Figure 8 shows the calculator display after the second cycle
of the division algorithm. The second coefficient of the quotient
has been computed to be "– 1" and
the corresponding portion of the division algorithm has been completed.
Press
 to move to Figure 9. to move to Figure 9. |
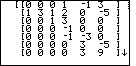
| In the earlier Figures we could see all that we needed to see on the
screen.
Now, in Figure 9, we can see some of the values but we are missing the
bottom numbers. Because the program is paused, we can use the cursor keys to
move around on the screen. For example,
we can press the  key to move down, as seen
in Figure 10. key to move down, as seen
in Figure 10.
|
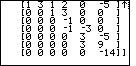
| Figure 10 displays the bottom of the matrix. Now that we can see the bottom of the matrix we note that the problem is done. If we press the ENTER the program will display the options to do a new problem, quit, or re-display the current matrix. |
Here is one more example:
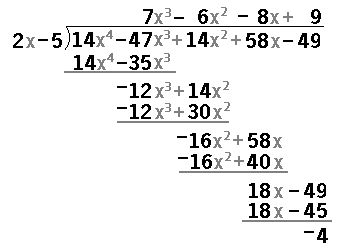

| In Figure 11 we have pressed  to ask for a new problem, and we have entered both
the DIVISOR LIST and the DIVIDEND LIST.
to ask for a new problem, and we have entered both
the DIVISOR LIST and the DIVIDEND LIST.
|
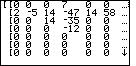
| Press  to move from Figure 11 to
Figure 12. Here we can see the matrix after the first step of the algorithm.
Unfortunately, we can only see the left side of the matrix.
We press the to move from Figure 11 to
Figure 12. Here we can see the matrix after the first step of the algorithm.
Unfortunately, we can only see the left side of the matrix.
We press the  key to move the
display to the right so that we can see the rest of the
DIVIDEND in Figure 13. key to move the
display to the right so that we can see the rest of the
DIVIDEND in Figure 13. |
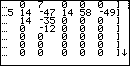
| Having seen the entire DIVIDEND,
we press  to continue the program. to continue the program.
|
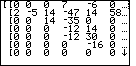
| Figure 14 shows the matrix after the second step of the division algorithm. The second coefficient of the quotient has been computed to be "– 6". |
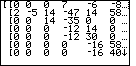
| To move from Figure 14 to Figure 15 we
press  to take the next step in the
algorithm. to take the next step in the
algorithm. |
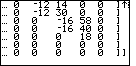
| Then, in Figure 16, we use the
 key to shift the display to the
right and the key to shift the display to the
right and the  key to shift the display down.
This allows us to look at all of the matrix. There is more to do for the problem.
Therefore, press the key to shift the display down.
This allows us to look at all of the matrix. There is more to do for the problem.
Therefore, press the  key to move to Figure 17. key to move to Figure 17.
|
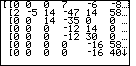
| At this point all of the updates from the program are happenning in matrix cells that are off the screen. We can use the cursor keys to move the display around so that we can see more of the matrix. |
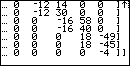
| Figure 18 shows the bottom right side of the matrix.
We press  one more time.
This will display the menu shown in Figure 19. one more time.
This will display the menu shown in Figure 19. |
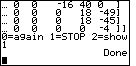
| Here we chose option 1 to end the program. Had we chosen option 2 the program would have re-displayed the matrix so that we could rove around it to see all of the values. |
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay