More on Graphing Parametrics
The textbook presents the following parametric equations.
x = 2 + t
y = 3 – t2
These equations are followed by a table that gives t values ranging from
– 3 to 3, in steps of 1.
| t | – 3 |
– 2 | – 1 |
0 | 1 | 2 |
3 |
| x | – 1 |
0 | 1 |
2 | 3 | 4 |
5 |
| y | – 6 |
– 1 | 2 |
3 | 2 | – 1 |
– 6 |
This is followed by the statement "The graph is a parabola",
along with a graph of a parabola.
However, the table only has seven sets of values, and a graph of those seven ordered pairs would appear as
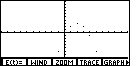 The seven points graphed above certainly lie on a parabola. We could generate
more points if we had expanded the table to have t increase in steps of 1/4,
thus generating 25 points. Such points are graphed as
The seven points graphed above certainly lie on a parabola. We could generate
more points if we had expanded the table to have t increase in steps of 1/4,
thus generating 25 points. Such points are graphed as
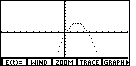 This is starting to look like a parabola. We could increase the number of points by
making t increase in steps of 0.05 to generate the graph
This is starting to look like a parabola. We could increase the number of points by
making t increase in steps of 0.05 to generate the graph
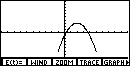 This graph has even more points, but it just
covers the x values between – 3
and 3. In order for us to have the calculator generate a parabola similar to the one shown in
the text we will need to have the value of t start at about – 4 and
increase up to about 4. Then, with the step increase set for 0.05,
the calculator would produce the graph
This graph has even more points, but it just
covers the x values between – 3
and 3. In order for us to have the calculator generate a parabola similar to the one shown in
the text we will need to have the value of t start at about – 4 and
increase up to about 4. Then, with the step increase set for 0.05,
the calculator would produce the graph
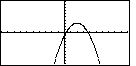 This is indeed similar to the graph given in the text.
This is indeed similar to the graph given in the text.
The text goes on to show that for the two parametric equations given above, we can
eliminate the parameter and produce the function
y = – x2 + 4x – 1
However, the graph of that function should be given as
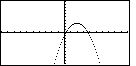 Note the difference between the last two graphs. The parametric equation graph seems thicker in some places,
and jagged at others. The graph of the function is the usual smooth, well-defined parabola, although
it appears here as a series of disconnected dots. Why is there a
difference?
Note the difference between the last two graphs. The parametric equation graph seems thicker in some places,
and jagged at others. The graph of the function is the usual smooth, well-defined parabola, although
it appears here as a series of disconnected dots. Why is there a
difference?
When graphing the function, the calculator uses the x-values associated with the
middle of each pixel moving across the entire screen. As a consequence, each column of pixels
has at most one pixel that is turned "black" because it is associated with the corresponding y-value.
The calculator used here was set to "DrawDot". Therefore, the graph is made up
of one dot per pixel-column for this
function.
On the other hand, the parametric graph lets t run from – 4 to 4 in steps of 0.05.
For each t-value the calculator produces an x-value and a y-value.
Then, the calculator identifies the appropriate pixel that contains the ordered pair (x,y).
In doing this it is entirely possible that two successive t-values would
produce x values that are associated with the same column of pixels, but where the
corresponding y-values are associated with different rows of pixels. Thus, in the
parametric graph, within a column of pixels we may find two pixels turned "black".
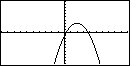
It is worth noting that this graph was also made with the "DrawDot" setting. The
large number of t-values means that the graph looks like a connected series of dots.
For completeness, the following graph was made for the function
y = – x2 + 4x – 1
but with the setting "DrawLine" turned on.
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay






