The ABC program on the TI-89

The Fall 1999, Section 06, precalculus class developed the following program as an aid in computing various quadratic characteristics from the coefficients, A, B, and C of the general quadratic equation y = Ax² + Bx + C We start with a listing of the program.

ABC program listing
for the TI-89

Right click abc.89p
for the TI-89 program

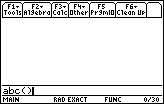
Then let us look at a few screens to show the program in action.

Figure 1	In Figure 1 we have entered abc() into the command line. We will need to press the key to start the program.
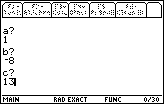
Figure 2	The program starts by asking for the values of A, B, and C, where it is understood that we are looking at the equation y = Ax² + Bx + C We press ENTER after each value.
Figure 3	Once the values have been entered, the program computes the y-coordinate of the y-intercept, and the coordinates of the vertex of the parabola. For the quadratic equation y = x² + ^–8x + 13 we have the y-intercept as (0,13) and the vertex at (4,^–3) The program is in a "paused" state at this point. We press the ENTER key to continue.
Figure 4	The ABC program continues by giving us the coordinates of the point symmetric to the y-intercept. In this case, that point is (8,13). Again the program is paused and we press ENTER to continue.
Figure 5	The program concludes by computing and displaying the value of the discriminant, 12, and then the x-coordinates of the x-intercepts. Because the discriminant in this case is positive, there are two real roots. Furthermore, because the value 12 is not a perfect square then those roots will be irrational. The program produces the values and Because the TI-89 used here was set to provide exact answers, these answers are given in radical form. The program has finished, but we are left in the ProgramIO screen.
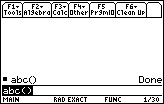
Figure 5a	In Figure 5a we return to the HOME screen by pressing the key. Note that the screen shows that the first run of the program completed. Now we need to press to run the program again.
Figure 6	Now we enter the coefficients for the equation y = 6x² + ^–13x + ^–70
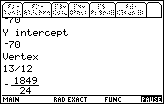
Figure 7	The program moves through the same steps and displays the appropriate values for the y-intercept and the vertex.
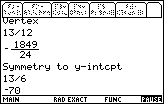
Figure 8	Figure 8 continues the output by showing the coordinates of the point symmetric to the y-intercept.
Figure 9	And, the program concludes by giving the value of the discriminant and the two x-intercepts, which in this case are rational values.
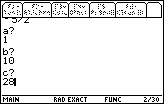
Figure 10	Figure 10 starts a new equations, namely, y = x² + 10x + 28
Figure 11	Figure 11 shows the y-intercept and the coordinates of the vertex.
Figure 12	Figure 12 gives the coordinates of the point symmetric to the y-intercept.
Figure 13	And, Figure 13 displays the discriminant, which in this case is –12, and, therefore, there are no real solutions, and no x-intercepts.