Figure 3

|
The only important point of this screen is that it shows the menu on the bottom line.
We would like
to check on the range of values, so we select the WIND
option by typing  .
This produces a screen similar to the following picture. .
This produces a screen similar to the following picture.
|
Figure 4
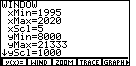
|
You may have different values. That is just fine because we will now set the values
to the ranges that we want.
Do this by using the cursor control keys to move up or down the list,
typing in new values where needed.
The following screen reflects a change of values that
will have x running from -1 to 20, and y going from -10 to 30.
|
Figure 4a
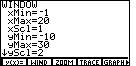
| Note that I chose the yMin to be -10,
even though our values do not go down that far.
The choice was made so that the y-axis would be elevated off the bottom of the
display. This helps later when the graph
is displayed and there are menus along the bottom of the screen
that cover up the graph.
By using -10 for yMin, the menus will be covering up areas that
are not important to the values being graphed.
There is one more value to display, as noted by the
down arrow at the left of "yScl".
That last value is "xRes" and it should be set to 1.
|
Figure 5

| Get out of the WIND display by using  .
This will take you back to a blank screen, as in Figure 2. Now use the .
This will take you back to a blank screen, as in Figure 2. Now use the
  buttons
to open the LIST menu.
This should produce a screen as seen to the left in Figure 5.
Note that the menu has the { and }
characters assigned to the buttons
to open the LIST menu.
This should produce a screen as seen to the left in Figure 5.
Note that the menu has the { and }
characters assigned to the  and and  keys,
repectively. Lists on the TI-86 are enclosed in curly braces.
There is no key assigned to the
curly brace. Thus, when we want to type a curly
brace we need to open the LIST menu so that we can use
the F1 and F2 keys. keys,
repectively. Lists on the TI-86 are enclosed in curly braces.
There is no key assigned to the
curly brace. Thus, when we want to type a curly
brace we need to open the LIST menu so that we can use
the F1 and F2 keys.
|
Figure 6

|
Now, use the  button to generate the left curly brace.
The screen shoud appear
as in Figure 6.
We will now complete the list which will hold our x values.
To do this
we type the elements of the list, separated by a comma.
In our example we want the values
5, 8, 9, 11, and 15.
So we enter button to generate the left curly brace.
The screen shoud appear
as in Figure 6.
We will now complete the list which will hold our x values.
To do this
we type the elements of the list, separated by a comma.
In our example we want the values
5, 8, 9, 11, and 15.
So we enter  
 
 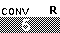
|
Figure 7
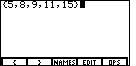
|
Then, to finish off the list, we will add the closing curly brace by typing
 . The result should be the screen to the left, in Figure 7.
Having created a list, we want to save it, or rather we want to STORE it in a variable.
The . The result should be the screen to the left, in Figure 7.
Having created a list, we want to save it, or rather we want to STORE it in a variable.
The  key generates the store arrow on the screen. key generates the store arrow on the screen.
|
Figure 8
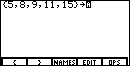
| Now we need to give the list a name. We will use L5 for this list.
The TI-86 has already moved into alphabetic mode as signaled by the
change in the cursor (the cursor was not captured in the image in Figure 8
but it appears as a flashing black box with a white uppercase A inside of it.
|
Figure 9

| To arrive at the name L5, press
 to produce the "L".
Then, to get out of alphabetic mode, press to produce the "L".
Then, to get out of alphabetic mode, press
 and follow that by
pressing and follow that by
pressing  .
This should leave the screen looking like Figure 9.
Finally, press .
This should leave the screen looking like Figure 9.
Finally, press  . .
|
Figure 10
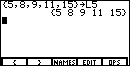
|
The TI-86 responds by displaying our L5
list as the answer, this time without the commas.
Now we need to enter the second list, the y values,
and store it in a variable we will call L6.
|
Figure 11
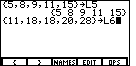
|
Use  to get the {, to get the {,
  
  and
and  to get the }.
Then, to get the }.
Then,
 
 
|
Figure 12
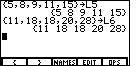
|
Use the  key to submit the new list. Again, the TI-86
responds by displaying the newly entered list, as in Figure 12. key to submit the new list. Again, the TI-86
responds by displaying the newly entered list, as in Figure 12.
|
Figure 13
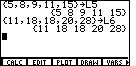
|
Now that the data has been entered, we need to use the statistical functions to do
the linear regression. Press   .
This will close the LIST menu of
Figure 12 and generate the STAT menu at the bottom of Figure 13. .
This will close the LIST menu of
Figure 12 and generate the STAT menu at the bottom of Figure 13.
|
Figure 13a
|
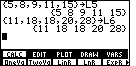
We want to do some calculations in the statistical area.
We use  to select CALC from the menu.
This will open a new menu, as in Figure 13a, that includes the
LinR command in the third position.
to select CALC from the menu.
This will open a new menu, as in Figure 13a, that includes the
LinR command in the third position.
|
Figure 14
|
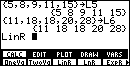
Press the  to generate the LinR
command. Figure 14 shows that "LinR" command on the screen,
just as if you had entered it
by keystrokes, which you could have done. to generate the LinR
command. Figure 14 shows that "LinR" command on the screen,
just as if you had entered it
by keystrokes, which you could have done.
|
The TI-86 wants to do statistical calculations using a list for
the
Figure 15
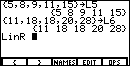
| We could type the names of the lists directly, or we could move back to the LIST
menu, select the NAMES sub-menu, and then select the lists from that display. We will
use this second approach. To get to the LIST menu press
  . This should produce the
screen in Figure 15. . This should produce the
screen in Figure 15.
|
Figure 16

|
To open the NAMES sub-menu, press  . Now there
should be two menus, as in Figure 16. Note that the particular arrangement
of lists in that bottom menu will change over time as new lists are created and
old ones are deleted. You may even need to use the . Now there
should be two menus, as in Figure 16. Note that the particular arrangement
of lists in that bottom menu will change over time as new lists are created and
old ones are deleted. You may even need to use the  key to look through a continuation of the menu if there are more than 5 LISTs.
Also, the TI-86 maintains 3 standard lists, xStat, yStat, and fStat.
key to look through a continuation of the menu if there are more than 5 LISTs.
Also, the TI-86 maintains 3 standard lists, xStat, yStat, and fStat.
|
Figure 17
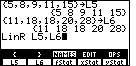
|
Press  
 to generate the L5,L6 as seen in Figure 17. to generate the L5,L6 as seen in Figure 17.
|
Figure 18
|
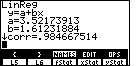
To do the specified linear regression, press  .
The TI-86 should respond with the screen shown in Figure 18. .
The TI-86 should respond with the screen shown in Figure 18.
|
For completeness, I have constructed the following table to show all of the
values that would have to be computed to use the formula given in the book.
 key to select the
desired option.
To get out of the review of modes, press the
key to select the
desired option.
To get out of the review of modes, press the  .
. 
 to display a screen similar to this.
to display a screen similar to this.

 key to select the
desired option.
To get out of the review of modes, press the
key to select the
desired option.
To get out of the review of modes, press the  .
. 
 .
This will bring up the graphing screen such as
.
This will bring up the graphing screen such as

 .
This produces a screen similar to the following picture.
.
This produces a screen similar to the following picture.
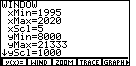
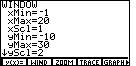

 .
This will take you back to a blank screen, as in Figure 2. Now use the
.
This will take you back to a blank screen, as in Figure 2. Now use the

 buttons
to open the LIST menu.
This should produce a screen as seen to the left in Figure 5.
Note that the menu has the { and }
characters assigned to the
buttons
to open the LIST menu.
This should produce a screen as seen to the left in Figure 5.
Note that the menu has the { and }
characters assigned to the  and
and  keys,
repectively. Lists on the TI-86 are enclosed in curly braces.
There is no key assigned to the
curly brace. Thus, when we want to type a curly
brace we need to open the LIST menu so that we can use
the F1 and F2 keys.
keys,
repectively. Lists on the TI-86 are enclosed in curly braces.
There is no key assigned to the
curly brace. Thus, when we want to type a curly
brace we need to open the LIST menu so that we can use
the F1 and F2 keys.

 button to generate the left curly brace.
The screen shoud appear
as in Figure 6.
We will now complete the list which will hold our x values.
To do this
we type the elements of the list, separated by a comma.
In our example we want the values
5, 8, 9, 11, and 15.
So we enter
button to generate the left curly brace.
The screen shoud appear
as in Figure 6.
We will now complete the list which will hold our x values.
To do this
we type the elements of the list, separated by a comma.
In our example we want the values
5, 8, 9, 11, and 15.
So we enter 





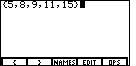
 . The result should be the screen to the left, in Figure 7.
Having created a list, we want to save it, or rather we want to STORE it in a variable.
The
. The result should be the screen to the left, in Figure 7.
Having created a list, we want to save it, or rather we want to STORE it in a variable.
The  key generates the store arrow on the screen.
key generates the store arrow on the screen.
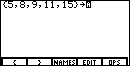

 to produce the "L".
Then, to get out of alphabetic mode, press
to produce the "L".
Then, to get out of alphabetic mode, press
 and follow that by
pressing
and follow that by
pressing  .
This should leave the screen looking like Figure 9.
Finally, press
.
This should leave the screen looking like Figure 9.
Finally, press  .
. 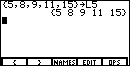
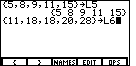
 to get the {,
to get the {,









 and
and  to get the }.
Then,
to get the }.
Then,




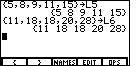
 key to submit the new list. Again, the TI-86
responds by displaying the newly entered list, as in Figure 12.
key to submit the new list. Again, the TI-86
responds by displaying the newly entered list, as in Figure 12.
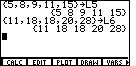

 .
This will close the LIST menu of
Figure 12 and generate the STAT menu at the bottom of Figure 13.
.
This will close the LIST menu of
Figure 12 and generate the STAT menu at the bottom of Figure 13.

 to select CALC from the menu.
This will open a new menu, as in Figure 13a, that includes the
LinR command in the third position.
to select CALC from the menu.
This will open a new menu, as in Figure 13a, that includes the
LinR command in the third position.

 to generate the LinR
command. Figure 14 shows that "LinR" command on the screen,
just as if you had entered it
by keystrokes, which you could have done.
to generate the LinR
command. Figure 14 shows that "LinR" command on the screen,
just as if you had entered it
by keystrokes, which you could have done.
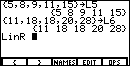

 . This should produce the
screen in Figure 15.
. This should produce the
screen in Figure 15.

 . Now there
should be two menus, as in Figure 16. Note that the particular arrangement
of lists in that bottom menu will change over time as new lists are created and
old ones are deleted. You may even need to use the
. Now there
should be two menus, as in Figure 16. Note that the particular arrangement
of lists in that bottom menu will change over time as new lists are created and
old ones are deleted. You may even need to use the  key to look through a continuation of the menu if there are more than 5 LISTs.
Also, the TI-86 maintains 3 standard lists, xStat, yStat, and fStat.
key to look through a continuation of the menu if there are more than 5 LISTs.
Also, the TI-86 maintains 3 standard lists, xStat, yStat, and fStat.



 to generate the L5,L6 as seen in Figure 17.
to generate the L5,L6 as seen in Figure 17.

 .
The TI-86 should respond with the screen shown in Figure 18.
.
The TI-86 should respond with the screen shown in Figure 18.
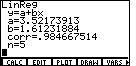

 will close the menu of Figure 18 and generate
the menu on Figure 18a.
will close the menu of Figure 18 and generate
the menu on Figure 18a.
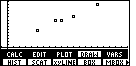
 . This will display the graph, as seen
in Figure 19.
. This will display the graph, as seen
in Figure 19.
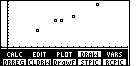
 to see more options.
This has been done to get to Figure 19a.
to see more options.
This has been done to get to Figure 19a.
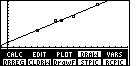
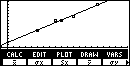
 to select DRREG. This draws the line described by the regression equation.
Now you can see the advantage of setting up the WIND values for
the graph back in Figure 4A, as well as setting the
yMin value to -10. The menu in Figure 19
covers the bottom of the graph, but we can still see the first quadrant. You might want to
look ahead at Figure 27, which corresponds to Figure 20, but with yMin set at 0.
to select DRREG. This draws the line described by the regression equation.
Now you can see the advantage of setting up the WIND values for
the graph back in Figure 4A, as well as setting the
yMin value to -10. The menu in Figure 19
covers the bottom of the graph, but we can still see the first quadrant. You might want to
look ahead at Figure 27, which corresponds to Figure 20, but with yMin set at 0.

 to
select the VARS option from the top menu of Figure 20, generating
Figure 21.
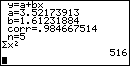
These variables represent such values as the mean of the x values, the
standard deviation of the x values (assuming x is a population), the
standard deviation of the x values (assuming x is a sample, and so on.
to
select the VARS option from the top menu of Figure 20, generating
Figure 21.
These variables represent such values as the mean of the x values, the
standard deviation of the x values (assuming x is a population), the
standard deviation of the x values (assuming x is a sample, and so on.

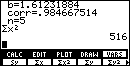
 to display more variables.
We want to see the sum of the x-square values. It is in this menu,
in position 3.
to display more variables.
We want to see the sum of the x-square values. It is in this menu,
in position 3.

 will select
that option, close the graph, and display
the symbol for the sum of the x-square values.
This is shown in Figure 23.
Press the
will select
that option, close the graph, and display
the symbol for the sum of the x-square values.
This is shown in Figure 23.
Press the  key to
perform the command, and move to Figure 24.
key to
perform the command, and move to Figure 24.

 .
Then, press
.
Then, press
 for the VARS, and then
for the VARS, and then
 to find more of the variables.
Now we can select any of the other variables.
to find more of the variables.
Now we can select any of the other variables.


 and
and