|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
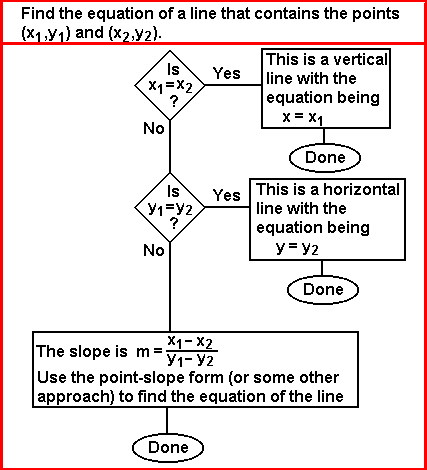
Such an algorithm can be programmed into the calculator. The SLOPE1 program on the TI-83 implements such an algorithm. Note that the SLOPE1 program uses the TOSTR program in order to generate nice looking output. The TI-83 version of the SLOPE1 program is available as slope1.83p. The version of TOSTR, presented in the 208304.htm page, is available as tostr.83p.
|
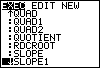
We can start by pressing the  key to open the PRGM menu.
Then we press the key to open the PRGM menu.
Then we press the  key to move the
highlight selector down to the SLOPE1 program.
The calculator used to generate Figure 1 holds a large
number of programs. Figure 1 shows the screen at the point where we have identified the SLOPE1 program. key to move the
highlight selector down to the SLOPE1 program.
The calculator used to generate Figure 1 holds a large
number of programs. Figure 1 shows the screen at the point where we have identified the SLOPE1 program.
|

| Once the SLOPE1 program was identified in Figure 1, we press the
 key to select that program and to paste
prgmSLOPE1 as a command on the screen, as shown in Figure 2. key to select that program and to paste
prgmSLOPE1 as a command on the screen, as shown in Figure 2.
We can execute the command and start running the program by
pressing the |
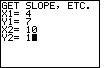
| In Figure 3, the program has started. The program clears the screen and
displays "GET SLOPE, ETC." on the top line, followed by a
prompt for the value of "X1" on the second line.
We are looking for the solution to "Find the equation of the line containing the points
  for X1.
The program accepts that value and continues by asking for the value
for Y1. for X1.
The program accepts that value and continues by asking for the value
for Y1.
  assigns 7 to Y1.
This is followed by assigns 7 to Y1.
This is followed by  
 to give X2 the value 10,
and to give X2 the value 10,
and  to leave the screen as it appears
in Figure 3. to leave the screen as it appears
in Figure 3.
|
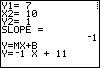
| We moved from Figure 3 to Figure 4 by
pressing the  key, and then waiting for the
calculator to do its work. In response the calculator computes the slope,
given as – 1 in Figure 4, and it then continues to generate the
slope-intercept form of the resulting equation. key, and then waiting for the
calculator to do its work. In response the calculator computes the slope,
given as – 1 in Figure 4, and it then continues to generate the
slope-intercept form of the resulting equation.
At that point the program is in a "paused" condition, waiting for us to press the ENTER key to continue. The "moving" line of dots in the upper right corner of the screen indicate that "paused" condition. We press |
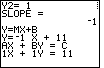
|
The program continues by computing and displaying the STANDARD form of the resulting equation.
Again, the program is "paused" at this point.
We press |
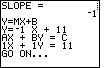
| Figure 6 again shows the program in a "paused" condition, where
the program has indicated that it is done with the current
problem and it is waiting to continue with the
next problem.
We press |
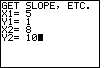
| The program has started over, from the beginning. The screen has been cleared,
the heading has been rewritten, and the program prompts for values of the coordinates of our
two points. In this case we are solving the problem:
"Find the equation of the line containing the points
 to accept the final value and move to Figure 8. to accept the final value and move to Figure 8.
|
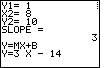
| The calculator has determined the slope and the slope-intercept form
of the solution. From the "paused" condition of Figure 8
we press the  key to move to Figure 9. key to move to Figure 9.
|
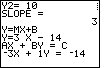
| Here the calculator has determined the standard form
of the solution equation.
Please note that the SLOPE1 program produces a standard form version of the equation that does not require the leading coefficient to be non-negative. Press the |
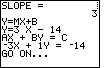
| The calculator has completed the problem, and it is ready to move on to the next
problem. Press the  key to move to Figure 11. key to move to Figure 11. |
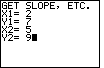
| Figure 11 represents the data input for yet another example:
"Find the equation of the line containing the points
|
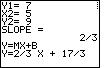
| The calculator has determined the slope between the two points to be
|
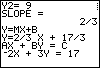
| Figure 13 contains the standard form of the solution equation. |
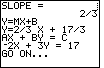
| The calculator has completed the problem, and it is ready to move on to the next
problem. Press the  key to move to Figure 15. key to move to Figure 15.
|
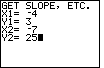
| Figure 15 represents the data input for yet another example:
"Find the equation of the line containing the points
|
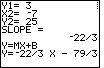
|
The calculator has determined the slope between the two points to be
|
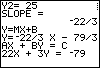
| Figure 17 contains the standard form of the solution equation. |

| The calculator has completed the problem, and it is ready to move on to the next
problem. Press the  key to move to Figure 19. key to move to Figure 19.
|
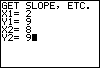
| Figure 19 represents the data input for yet another example:
"Find the equation of the line containing the points
|

| The SLOPE1 program correctly identifies the equation as the constant function,
with the solution equation being Y=9.
Note that we could write this as Y=0X+9 to produce the strict slope intercept form.
In addition we could write this as |
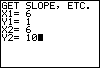
| Figure 21 represents the data input for yet another example:
"Find the equation of the line containing the points
|

| The SLOPE1 program correctly identifies the equation as a vertical line
with the solution equation being X=6.
Note that we could write this as |
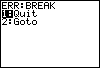
| If we want to stop the program we need to break out of it. We can press the
 key to break out of the program.
The result is shown in Figure 23.
There are only two options. Either we can GOTO or QUIT. We want to
QUIT, so we press the key to break out of the program.
The result is shown in Figure 23.
There are only two options. Either we can GOTO or QUIT. We want to
QUIT, so we press the  key to move to Figure 24. key to move to Figure 24.
|

| Figure 24 looks remarkably similar to Figure 22. However, in Figure 22 the calculator was in a "paused" condition. In Figure 24 we are out of the program and ready to do anything that we want to do. |
The SLOPE1 program is designed to generate an equation if we are given the coordinates of two points on the line. How can we use the SLOPE1 program to solve problems such as
| Find the equation of the line that has slope=4/7 and that contains the point (9,6). |
| M = | 4 | = | change in y |
| 7 | change in x |
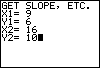
| Figure 25 shows that the program has been restarted.
Having broken out of the program in Figures 23 and 24, we only needed to
press the  key to re-issue the
the last command, namely prgmSLOPE1, and therefore restart the program.
In Figure 25 we have entered the two points derived from the discussion above.
We can press key to re-issue the
the last command, namely prgmSLOPE1, and therefore restart the program.
In Figure 25 we have entered the two points derived from the discussion above.
We can press  to accept the value for y2 and
to move to Figure 26. to accept the value for y2 and
to move to Figure 26. | |||||||||
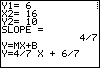
| The first thing to notice in Figure 26 is that the slope has been computed to be exactly the value given in the problem statement. This is verification that we have correctly computed the coordinates of the second point. Then we can look at the slope-intercept form for the desired equation. | |||||||||
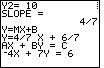
| Figure 27 gives the standard form of the equation. | |||||||||
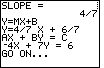
| The calculator has completed the problem, and it is ready to move on to the next
problem. Press the  key to move to Figure 29. key to move to Figure 29.
| |||||||||
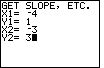
| The next problem to consider is
| |||||||||
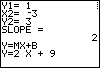
| Figure 30 confirms the second point by calculating the expected slope. Then, the SLOPE1 program produces the slope-intercept form of the desired equation. | |||||||||
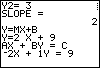
| Figure 31 gives the standard form of the equation. | |||||||||
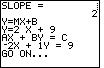
| The calculator has completed the problem, and it is ready to move on to the next
problem. Press the  key to move to Figure 33. key to move to Figure 33.
| |||||||||
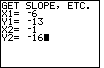
| The next problem to consider is
| |||||||||
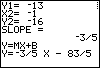
| Figure 34 confirms the second point by calculating the expected slope. Then, the SLOPE1 program produces the slope-intercept forms of the desired equation. | |||||||||
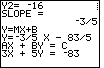
| Figure 35 gives the standard form of the equation. | |||||||||
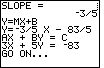
| The calculator has completed the problem, and it is ready to move on to the next problem. |
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay