|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
We need to pay attention to the use of irrational numbers on the TI-83. We will focus on the square root function.

|
To get the square root symbol, which is above the x2 key,
press the  key and then the key and then the 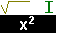 key.
Your screen should then appear as in Figure 1. key.
Your screen should then appear as in Figure 1.
|

| If we want the square root of 2 then we need to complete the problem by
pressing first the  and then
the and then
the  key.
Then we can submit the problem by pressing the key.
Then we can submit the problem by pressing the
 key to make the screen appear as in Figure 2. key to make the screen appear as in Figure 2.
Note that 1.414213562 is only an approximation to the square root of 2. Furthermore, as in the page about rational values, the calculator actually carries internally a few more digits to this approximation. |
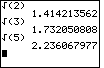
| Figure 3 duplicates the figure found in the text book for the roots of 2, 3, and 5. |

| Merely taking the square root does not ensure that we have
an irrational number. The square root of 4 is 2 (since 2*2 is 4), and 2 is a rational
number. Therefore the square root of 4 is merely another name for the rational
number 2.
Figure 4 concludes with a problem where we ask the calculator to multiply the square root of 5 times itself. Fortunately, the answer is 5. But how can this be? After all, we know that the calculator only approximates the square root of 5. The value that we found in Figure 3, namely 2.236067977, is not the square root of 5. It is just very close to the true value. So how does the calculator multiply the square root of 5 by itself and get an answer of 5? It does this because it kept those extra digits and because using those extra digits and then rounding the resulting answer off to 10 significant places yields the value 5. |

| We can check on the discussion of Figure 4 by multiplying the exact value 2.236067977
times itself.
We do this in Figure 5, and the result is definitely not 5. (It is also not 4.999999998.
After all, 2.236067977 has 9 places to the right of the decimal. If we really multiply it
by itself, the result will have 18 places to the right of the decimal and the rightmost
digit will be a 4, the result of 8*8.)
Figure 5 continues by recalculating the value of the square root of 5. Notice that the
closing parenthesis is not needed.
We merely used the keys |

| The answer from the last step in Figure 5 starts with the integer
value 2236. We subtract that from the answer. The new answer still has 10 digits, but the
four rightmost digits, 4998, are new. We have uncovered the extra digits from the calculation
of the value of the square root of 5. Let us repeat the process. Multiply the answer by 1000 to move the decimal point. |
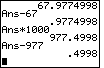
| Now subtract the resulting integer portion of the answer, in this case 67. There are no more hidden digits to expose so we only have 7 digits in the answer. We can do the process again, and we end up with a mere 4 digits in the answer. |
It is important to remember that the calculator is giving approximations to irrational values. The calculator maintains some extra digits of the answer, and uses those to help make it look like the calculator is really using the correct value.
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay