|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
|
Note that the TI-83 and the TI-83 plus have slightly different keys. This page uses the
keys associated with the TI-83. The differences are
that the TI-83 |
We need to pay attention to the use of rational numbers on the TI-83.
For one thing, unlike many less expensive calculators, the TI-83
does not have an ![]() key to deal with fractions.
This page presents the TI-83 approach to using rational numbers.
key to deal with fractions.
This page presents the TI-83 approach to using rational numbers.
We start by assuming that you have turned on the calculator. (Press
the ![]() key. If there is text on
the screen, you can clear the screen by pressing the
key. If there is text on
the screen, you can clear the screen by pressing the ![]() key.)
key.)

|
To generate the first screen, press the
|
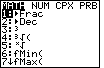
| Figure 2 shows the math menu. As it turns out,
the item that we want is the first item in the list. It is already highlighted.
Therefore, all we need to do is to press the  key to insert the
key to insert the |

| This figure shows the result of our efforts. We are asking the calculator to change
0.5 into a fraction. We press the  to signal that we are
done and that the calculator should carry out the instruction. to signal that we are
done and that the calculator should carry out the instruction.
|

| Figure 4 shows the calculator's response. |
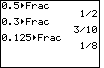
| We change Figure 4 into Figure 5 by using the keystrokes




 to produce the 0.3 to produce the 0.3


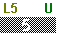


 to produce the 1/8 result. This is the screen that appears in the text.
to produce the 1/8 result. This is the screen that appears in the text.
|
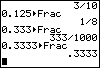
| The text goes on to point out that the
 the calculator responds with
333/1000, as seen in the middle of Figure 6. However, if we add one more digit so that we
enter .3333 the calculator responds with
333/1000, as seen in the middle of Figure 6. However, if we add one more digit so that we
enter .3333 then the
calculator refuses to convert to a fraction and instead displays the result as a decimal, as
shown in the bottom of Figure 6. then the
calculator refuses to convert to a fraction and instead displays the result as a decimal, as
shown in the bottom of Figure 6.
|
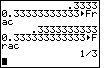
| Figure 7 demonstrates that we can fool the calculator. At the top of Figure 7 we have tried to convert 0.33333333333 to a fraction. The calculator refuses to do this and, instead, displays the value as a decimal. However, if we add one more digit, so that we have 12 three's, then the calculator incorrectly converts this to 1/3. Essentially, the calculator determines that it can not tell the difference between 0.333333333333 and 1/3. Therefore, the calculator has no problem making the conversion, even though it is wrong. The two values are close, in fact, very close, but they are not the same. |

| Figure 8 explores some more of the concepts of rational numbers. In this figure we look
at the decimal expansion of 5/11, 5/7, and 8/13. It is important to note a few things here.
First, these are all repeating decimals.
The problem that we saw with 5/11 shows up again in 5/7 and in 8/13. The true equality for the former is 8/13 produces a similar, incorrect, rounded answer. |

| Figure 9 demonstrates another problem caused by the limited number
of digits that the calculator uses. The change from Figure 8 to Figure 9 is the
addition of a new problem, namely, 2/17.
Back when we did 8/13 the calculator gave an approximation, but it was enough
for us to correctly guess that the true answer is
|
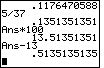
| Figure 10 starts a sequence of 5 frames that demonstrate how we can "see" the extra
digits that the calculator keeps. We start with 5/37, which the calculator displays
as the decimal .1351351351. Then we multiply this by 100. It is importnat to
note that we are not multiplying 0.1351351351
by 100, but rather that we are multiplying the previous answer by 100.
We can do this in two ways. For the first method, we can recall
the previous answer by using the keys

 . Then we use the keys . Then we use the keys

  
 .
Notice that the result has exactly the same number of digits showing. .
Notice that the result has exactly the same number of digits showing.
We can use the second method to do the next step, subtract 13 from the result.
For this we press the |
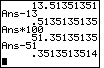
| In Figure 11 we will continue the process that we used in Figure 10, namely, multiply the old answer buy 100 to shift the decimal point two places to the right, and then subract the whole number part of the answer. Again, new values appear at the right end of the final answer in Figure 11, and those values are still part of the extra internal digits in the calculator. |

| In Figure 12, we apply the process yet another time, but this time we get different results. Multiplying by 100 accomplishes shifting the decimal point. However, when we subtract the 35 no new values are added to the right of our answer. We are now down to an 8 digit answer. |

| This new situation continues in Figure 13 where we drop down to a mere 6 digits in the answer. |

| And, for a last look, Figure 14 applies the technique one more time and we are down to a mere 4 digits. |

| Entering a mixed number into the calculator is a pain. In
Figure 15 we duplicate the steps from the text.
Specifically, to enter 41/2
we use the keys 

 
 .
Then we press the .
Then we press the  to accept our input and produce the answer,
"4.5". We can change this to a fraction by "recalling" the problem via the to accept our input and produce the answer,
"4.5". We can change this to a fraction by "recalling" the problem via the

 Then we can move to the math menu and select the
Then we can move to the math menu and select the
 and the and the  keys.
That results in the input line which we terminate via keys.
That results in the input line which we terminate via
 to produce the result 9/2. to produce the result 9/2.
Notice that we run into a problem if we try to do the same thing for -41/2. The calculator does exactly what we asked it to do, namely, add 1/2 to -4. The result is -3.5 or -7/2.
Be careful when entering -4! The appropriate key for the negative sign
is the |

| There are two methods for entering -41/2. First, we can recognize that we are really talking about -4 minus 1/2, and we enter the value in that fashion. Second, we can express the value as the negative of the quantity 4 and 1/2. Figure 16 shows both methods. |

Clearly the easiest way is to transfer the program between calculators.
The calculator that was used to prepare these figures has other programs in it. They are not needed and they do not affect the QUOTIENT program.
The QUOTIENT program was written to overcome the problem that we experienced in Figure 9. At that point we learned that the fraction 2/17 can not be displayed as a decimal value using the normal calculator functions. With 17 in the denominator, this fraction has a repeating sequence of digits that is 16 digits long. With the QUOTIENT program we will be able to look at the decimal representation of fractions that have long sequences of repeating digits.
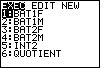
| To run a program on the TI-83 we enter the PRGM menu via the
 key. The resulting display depends upon the
programs that have been loaded into the calculator. Figure 17 identifies that there are
6 programs loaded into this particular calculator. The one we want is QUOTIENT, however,
in Figure 17, the first program, BAT1F, is selected. key. The resulting display depends upon the
programs that have been loaded into the calculator. Figure 17 identifies that there are
6 programs loaded into this particular calculator. The one we want is QUOTIENT, however,
in Figure 17, the first program, BAT1F, is selected.
|

| We can use the  key five times to
move the selection to the QUOTIENT program and then we can
use the key five times to
move the selection to the QUOTIENT program and then we can
use the  key to choose the selected program.
Alternatively, we could have simply pressed the key to choose the selected program.
Alternatively, we could have simply pressed the
 key to choose the program in position 6.
Either method results in Figure 19. key to choose the program in position 6.
Either method results in Figure 19.
|

| Figure 19 contans the cryptic command that the TI-83 uses
to start a program. Our response is the press the  key to actually start the program.
key to actually start the program. |

| At the start of the program, the screen clears and the user is prompted for a value for the numerator. |
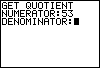
| For this example, we will choose the numerator to be 53. We then press
the  key and the program asks for a value for the denominator. key and the program asks for a value for the denominator. |
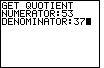
| We have chosen the denominator to be 37 so we are looking for the decimal representation of 53/37. Had we done this without the program the calculator would respond with 1.432432432, which we recognize from the earlier Figures to be the calculator's approximation to the true value. |
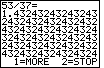
| We move to Figure 23 by pressing the  key.
The program reproduces the problem on the top line and then computes each digit of
the answer below. Since this is a repeating decimal, there is no nice place to stop.
When the calculator runs out of space, as it has done on the bottom of Figure 23,
the program asks if we want to get more of the answer, or do we want to stop? We
can see that the pattern just keeps going, so we will press the key.
The program reproduces the problem on the top line and then computes each digit of
the answer below. Since this is a repeating decimal, there is no nice place to stop.
When the calculator runs out of space, as it has done on the bottom of Figure 23,
the program asks if we want to get more of the answer, or do we want to stop? We
can see that the pattern just keeps going, so we will press the
 key to stop working on this problem. key to stop working on this problem.
|

| The program stops and returns to accept a new numerator and denominator. In Figure 24 those have been entered as 5 and 43, respectively. We might add that 5/43 on the calculator produces the approximate answer 0.1162790698. |

| Press  to leave Figure 24 and generate
Figure 25. Here we can see a more extended decimal representation of the value
5/43. We note that it repeats a pattern of digits, "116279069767441860465".
Since we do not need to see more of the value, we again select to leave Figure 24 and generate
Figure 25. Here we can see a more extended decimal representation of the value
5/43. We note that it repeats a pattern of digits, "116279069767441860465".
Since we do not need to see more of the value, we again select
 to stop working on this problem. to stop working on this problem. |
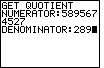
| Figure 26 starts yet another example. This time we have a denominator of 289. |
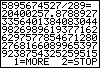
| The program gives the start of the decimal equivalent to 5895674527/289.
In examining the decimal version we can not pick out a repeating pattern. Therefore,
we can choose the  key at the bottom to let the process continue. key at the bottom to let the process continue. |

| Here we have move of the decimal expansion of our fraction. We still do not find the pattern repeating. Therefore, we can go on to look at more of the expansion. |

| More and more numbers. Can we find a repeating pattern? Possibly. The final seven digits on this screen, 8788927, are exactly the same as the digits immediately after the decimal point back in Figure 27. We will go on to another screen just to confirm that this is a repeating pattern. |

| Figure 30 essentially confirms that we have found the pattern. It took 272 digits before the pattern repeats. |
|
So far we have seen how to start the program, Figures 17-19, how to enter
values for the numerator and denominator, how to read the program
output and to ask for additional screens of output, and how to stop the
current problem and start over with a new numerator and denominator.
At some point, however, we want to end the program.
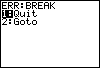
We break out of the program by pressing the
DANGER: if you choose the Goto command, then calculator will place you into the edit mode for changing the program QUOTIENT. This is fine if you know what you are doing. However, it is also a danger because any change that you make is automatically saved and there is no "undo" capability. In short, it is extremely easy to destroy a program once you are in edit mode. If you do destroy it, then the easiest fix is to reload the program from some other calculator. |
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay