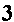 |
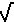  |
One of the topics in algebra, precalculus, and Calculus is rationalizing the denominator, or in some cases, rationalizing the numerator, of a fraction. For example, if we have a fraction such a
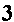 |
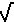  |
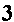 |
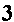 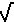  |
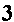 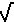  |
||
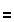 |
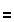 |
|||
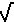  |
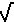  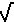  |
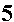 |
This skill seems a bit strange when we start using a calculator. After all, the calculator is just as happy to do the original problem as it is to evaluate the "rationalied" form. For example, the following screen image, from a TI-83, shows both fractions being evaluated to 1.341640786.
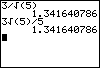
This skill is not just a new torture of mathemtics. There are actually some problems in Calculus that take advantage of the rationalizing the denominator or the numerator. However, the skill of rationalizing denominators used to be important long before we study and learn Calculus. We used to teach this skill because it greatly simplified evaluating expressions. This was at a time when we did not have calculators to do the arithmetic. At that time we had tables of square roots. We would look up the square root of 5 and find that 2.236 is a good approximation. If we were to try to evaluate the original problem we would have to divide 3 by 2.236, and that is an ugly, messy task. However, if we "rationalize" the denominator for the original problem to produce
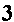
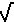

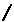
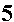
PRECALCULUS: College Algebra and Trigonometry
© 2000 Dennis Bila, James Egan, Roger Palay