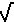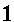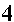One of the more common errors that students make in rationalizing higher roots is that the student applies the skills of rationalizing square roots without appreciating the real process being used. Thus, for the problem that requires us to rationalize the numerator of

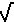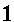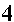we would multiply both numerator and denominator by 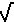to give

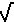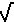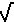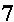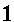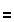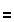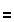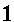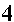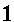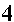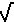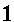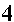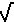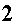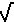Then, for the problem of rationalizing the numerator for

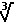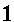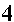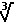
the temptation is to multiply both numerator and denominator by . However, this is not what we need to do.

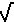
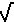
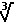
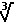
In the square root problem we needed to multiply by in order to get the square root out of the numerator. In this new cube root problem we need to multiply by something so that we can remove the cube root. We need to produce a numerator that is the cube root of 7 cubed. Thus, we need to multiply both the numerator and the denominator by , as in

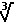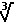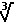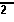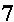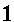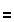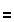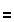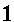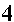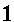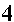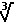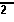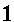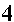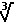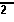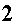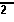The goal of the multipliction is to eliminate a root from the numerator (or from the denominator, as the problem dictates). We need to choose the value so that we end up with the n^th root of a value to the n^th power.