Remember that the TI-89 is case-insensitive. Although we may refer to the program as SM2,
on the TI-89 this is the same as sm2.
The problem that we will solve on the calculator is taken from page 233 of the text.
We need to give the program the constraints in matrix form. We can do this in two different ways.
First, we can merely type the matrix using the "[" and "]" characters. This is the
method that we used in Figure 3. Second, if we had stored the matrix
earlier under a name, then we could just enter the name. We will use that method for the
second problem, starting in Figure 22.
Right now, we need to remember how to create the augmented matrix for the constraints.
To do this we will re-write the constraints with each variable represented in the
inequality. (Note: we are not adding the "slack variables" here; the program will
do that for us. We are just making sure that each variable appears in each inequaltiy.]
Figure 4
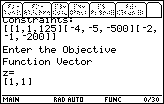
| We complete Figure 3 by pressing the  key.
The program now asks for the "Objective Function Vector".
We should note that on
the TI-89 there is no special form for a vector. A vector is treated as a single
row matrix, and, we do not need to put the extra set of brackets around that row.
For our problem, that objective function vector is
made up of the objective function coefficients. Since our objective function is
z = 1x1 + 1x2
the vector would be [1,1]. We enter this via the keys key.
The program now asks for the "Objective Function Vector".
We should note that on
the TI-89 there is no special form for a vector. A vector is treated as a single
row matrix, and, we do not need to put the extra set of brackets around that row.
For our problem, that objective function vector is
made up of the objective function coefficients. Since our objective function is
z = 1x1 + 1x2
the vector would be [1,1]. We enter this via the keys
 
  .
This produces the text seen in Figure 4. .
This produces the text seen in Figure 4.
|
Figure 5

| Pressing  to accept the
objective function vector of Figure 4 produces the
minimize vs. MAXIMIZE choice. We select the MAXIMIZE
option by pressing the to accept the
objective function vector of Figure 4 produces the
minimize vs. MAXIMIZE choice. We select the MAXIMIZE
option by pressing the  key to complete Figure 5. key to complete Figure 5.
|
Figure 6
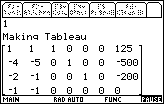
| After Figure 5 we have given the program all of the data
that it needs to do the problem. We press the  key to start the process. Along the way the calculator will display intermediate results.
At times it will pause to let us read those results. The first pause is shown in
Figure 6. Here, the calculator has created the TABLEAU and is displaying it
for us.
key to start the process. Along the way the calculator will display intermediate results.
At times it will pause to let us read those results. The first pause is shown in
Figure 6. Here, the calculator has created the TABLEAU and is displaying it
for us. |
Figure 7
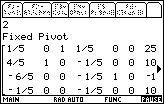
| The calculator was paused at Figure 6 to allow us to examine the TABLEAU.
We did so, and then we press the  key to continue the
program. The calculator entered the "Preprocessing" phase of the algorithm.
In that phase, the calcualtor identified the second row as the work row (not shown), and
within that second row, it identified the second column as the work column.
That means that the value that was in row 2 column 2, namely -5, becomes a
pivot point. Therefore, we use the second elementary row operation to
change it to a 1, and the third elementary
row operation to convert all remaining elements in the second column to be 0.
The calculator has done exactly that, and it has paused at that point to
display the resulting matrix, shown in Figure 7. This matrix corresponds
to the one in the middle of page 234 in the text.
Note that the entire matrix does not fit on the page. The heavy arrow
at the right side of the screen
indicates that there is more to be displayed. key to continue the
program. The calculator entered the "Preprocessing" phase of the algorithm.
In that phase, the calcualtor identified the second row as the work row (not shown), and
within that second row, it identified the second column as the work column.
That means that the value that was in row 2 column 2, namely -5, becomes a
pivot point. Therefore, we use the second elementary row operation to
change it to a 1, and the third elementary
row operation to convert all remaining elements in the second column to be 0.
The calculator has done exactly that, and it has paused at that point to
display the resulting matrix, shown in Figure 7. This matrix corresponds
to the one in the middle of page 234 in the text.
Note that the entire matrix does not fit on the page. The heavy arrow
at the right side of the screen
indicates that there is more to be displayed. |
Figure 8
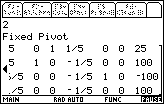
| We have moved from Figure 7 to Figure 8 by pressing the
right cursor key,  , to move over on the display.
Comparing Figure 8 with Figure 7 we can see the values that were cut off in Figure 7. , to move over on the display.
Comparing Figure 8 with Figure 7 we can see the values that were cut off in Figure 7. |
Figure 9

| We leave Figure 8 by pressing the  key
to continue the program. The calculator continues the preprocessing
phase, identifying the third row and first column as the work row and column.
It then changes the pivot point to a 1, and converts the remaining work column
values to 0. Again, we pause to examine the matrix, shown in Figure 9.
This matrix corresponds to the bottom matrix on page 234. key
to continue the program. The calculator continues the preprocessing
phase, identifying the third row and first column as the work row and column.
It then changes the pivot point to a 1, and converts the remaining work column
values to 0. Again, we pause to examine the matrix, shown in Figure 9.
This matrix corresponds to the bottom matrix on page 234.
|
Figure 10

| Figure 10 shows more of the matrix from Figure 9.
In this case, again, we used the cursor key to move to the
right. However, as we examine Figure 10 we note that part of the
top row of values has been cut off. |
Figure 11

| Figure 11 is the result of using the cursor up key,
 , and the , and the  key to move back to the upper left corner of the matrix.
key to move back to the upper left corner of the matrix.
|
Figure 12

| Figure 12 is the result of using the
 key to move to the next step. Unfortunately,
some of the output of the program has scrolled off the screen, and we have
no way to return to it.
The program has
looked at the matrix and determined that we are done with the preprocessing
phase. It indicated that fact in the message that is no longer visible,
and it displays the same matrix again, as in Figure 12. key to move to the next step. Unfortunately,
some of the output of the program has scrolled off the screen, and we have
no way to return to it.
The program has
looked at the matrix and determined that we are done with the preprocessing
phase. It indicated that fact in the message that is no longer visible,
and it displays the same matrix again, as in Figure 12. |
Figure 13

| The  key leaves Figure 12 and moves the
calculator into the basic algorithm. Here the calculator determines that the
fourth column is the work column, and that the first row is the work row.
The calculator makes the element in row 1 column 4 become 1 and the calculator
uses that 1 to change the other elements in that column to be 0.
Once this is done, the calculator displays the resulting matrix and pauses
to allow us to examine it, as shown in Figure 13. key leaves Figure 12 and moves the
calculator into the basic algorithm. Here the calculator determines that the
fourth column is the work column, and that the first row is the work row.
The calculator makes the element in row 1 column 4 become 1 and the calculator
uses that 1 to change the other elements in that column to be 0.
Once this is done, the calculator displays the resulting matrix and pauses
to allow us to examine it, as shown in Figure 13. |
Figure 14

| Pressing the  key continues the algorithm.
The calculator determines that we are done. It gives the message that the final
matrix is being displayed and it pauses as in Figure 14. key continues the algorithm.
The calculator determines that we are done. It gives the message that the final
matrix is being displayed and it pauses as in Figure 14. |
Figure 15

| Now we can get the calculator's best guess at the results by pressing the
 key. The program responds by indicating that the
maximum value for the objective function can be
found when x1 has the value 75.
This is exactly the value presented in the second sentence of the paragraph at the bottom
of page 234. The other values follow in Figures 16 and 17, with the value of the
objective function being given in Figure 18. key. The program responds by indicating that the
maximum value for the objective function can be
found when x1 has the value 75.
This is exactly the value presented in the second sentence of the paragraph at the bottom
of page 234. The other values follow in Figures 16 and 17, with the value of the
objective function being given in Figure 18.
|
Figure 16
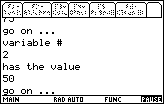
| We continue by pressing the  key,
to find, in Figure 16, that the
value of x2 needs to be 50. key,
to find, in Figure 16, that the
value of x2 needs to be 50. |
Figure 17

| Another  key shows us Figure 17, whcih gives us
s2, the second slack variable, having the value 50. key shows us Figure 17, whcih gives us
s2, the second slack variable, having the value 50. |
Figure 18

| Yet another  key moves us to Figure 18, which repeats
that the objective function value will be 125. key moves us to Figure 18, which repeats
that the objective function value will be 125. |
Figure 19

| For a convenience, the program continues, after a press of the
 key, to redisplay the matrix, as shown in Figure 19.
The program is paused at that point so that we can scroll over on the matirx if need be.
In this case the entire matrix is displayed on screen so we do not need to scroll
at all. However, notice the key, to redisplay the matrix, as shown in Figure 19.
The program is paused at that point so that we can scroll over on the matirx if need be.
In this case the entire matrix is displayed on screen so we do not need to scroll
at all. However, notice the  at the lower right
of the screen. This indicates that we are still in the sm2 program.
In addition, note that all of the menu items at the top of the screen
are unavailable in Figure 19. at the lower right
of the screen. This indicates that we are still in the sm2 program.
In addition, note that all of the menu items at the top of the screen
are unavailable in Figure 19. |
Figure 20
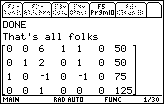
| Pressing of the
 key allows the program to end, as is
shown in Figure 20. However, we are still in the PROGRAM screen.
We do have a new option in that the F5 menu item is now available, as noted at the
top of the screen. key allows the program to end, as is
shown in Figure 20. However, we are still in the PROGRAM screen.
We do have a new option in that the F5 menu item is now available, as noted at the
top of the screen. |
Figure 21
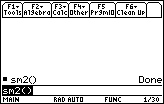
| We return to the HOME screen by pressing the
 key. Figure 21 shows that HOME screen with
The sm2() program marked as done, and with the sm2() item pre-loaded in the
command line. key. Figure 21 shows that HOME screen with
The sm2() program marked as done, and with the sm2() item pre-loaded in the
command line. |
One of the problems with the approach shown above is that
there is no asy recovery if you have made an error
in the original matrix, or in the objective function vector.
The program merely continues, and probably produces the wrong answers.
It is much safer for us to store the constraint matrix and the objective vector on
the calculator before we use SM2. That way, if an error is found, we can correct it
and rerun the program without having to re-enter all of the coefficients and constants.
We will demonstrate this in the remaining Figures.
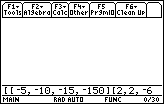
The next example is taken from page 238 of the text. In this case there are three
variables and two constraints. The problem is stated as:
Figure 22
|
The first step is to create the constraint matrix. The key strokes
 
 
 
 
  produce the command line shown in Figure 22. We stop here only to demonstrate
that as we add more to the input line, in Figure 23, part of the command
line scrolls off the left end as new characters are added to the right.
produce the command line shown in Figure 22. We stop here only to demonstrate
that as we add more to the input line, in Figure 23, part of the command
line scrolls off the left end as new characters are added to the right.
|
Figure 23
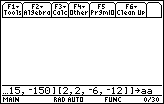
|
We complete the matrix via the keys 
 
  to complete the entry of the matrix. To
save it under a name we use the to complete the entry of the matrix. To
save it under a name we use the  key followed by
the desired name. In the example shown in Figure 23, that name is aa, and was created via the key followed by
the desired name. In the example shown in Figure 23, that name is aa, and was created via the
 
  key sequence. key sequence.
|
Figure 24
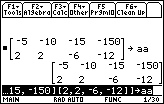
| Pressing the  key to accept the command causes the
display to change to that shown in Figure 24. key to accept the command causes the
display to change to that shown in Figure 24. |
Figure 25

| In Figure 25
we will enter the objective vector and save it under the name bb. Again, remember that on
the TI-89 a vector is just a single row matrix.
A small warning: this is not the right set of values, but we will enter them here,
use them, discover our error, correct them, and rerun the program with the correct
values. The keys
 
  produce the
vector. Note the single left and right square bracket. Then we
store the vector in bb via the keys produce the
vector. Note the single left and right square bracket. Then we
store the vector in bb via the keys

 
  and and  .
We finish Figure 25 by typing the name of the program including the parentheses,
using the key sequence: .
We finish Figure 25 by typing the name of the program including the parentheses,
using the key sequence:
 
 
  . .
|
Figure 26

| The program starts as before, asking for the number of variables, we respond with
  , and
the number of constraints, to which we respond with , and
the number of constraints, to which we respond with
 . . |
Figure 27

| We leave Figure 26 via the  key.
The program responds with a request for the matrix of constraint coefficients and constants.
In this case,
we have already entered that matrix and we have saved it under the name
aa. Therefore, we type the name of the matrix via the key.
The program responds with a request for the matrix of constraint coefficients and constants.
In this case,
we have already entered that matrix and we have saved it under the name
aa. Therefore, we type the name of the matrix via the
 
  keys.
We press keys.
We press  to accept that answer. The program asks for the Function Vector.
We respond with the name of the single row matrix that we saved earlier: to accept that answer. The program asks for the Function Vector.
We respond with the name of the single row matrix that we saved earlier:
 
  . This completes Figure 27. . This completes Figure 27.
|
Figure 28

| Having pressed  to accept the name of
the Function Vector, the program asks if we want to minimize or MAXIMIZE that
function. In this case we want ot "minimize" the result so we press the to accept the name of
the Function Vector, the program asks if we want to minimize or MAXIMIZE that
function. In this case we want ot "minimize" the result so we press the
 key. key.
|
Figure 29
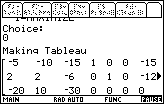
| Again we press the  keys to accept the 0 in Figure 28.
The program goes on to show the initial Tableau, as shown in Figure 29.
We can
compare this to the matrix on page 239. It is almost the same. However,
we note that the signs on the values in the bottom row are reversed. What happened? keys to accept the 0 in Figure 28.
The program goes on to show the initial Tableau, as shown in Figure 29.
We can
compare this to the matrix on page 239. It is almost the same. However,
we note that the signs on the values in the bottom row are reversed. What happened?
If we go back we will find that we created the objective function vector
using the equation
Z = -20x1 + 10x2 - 30x3
We created Z = -z as was done in the book. However, the program, SM2,
does this for us when we select the "minimize" option. Therefore, SM2
has undone our conversion, and the values in the final row of the TABLEAU have the wrong sign.
We need to stop the program, change the vector and then run the program again with the
new vector.
|
Figure 30
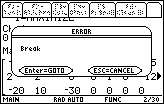
| We stop the program by pressing the  key.
The calculator responds with Figure 30. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the CANCEL menu item.
To do this we press the key.
The calculator responds with Figure 30. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the CANCEL menu item.
To do this we press the  key. key. |
Figure 31

| Figure 31 shows the Program IO screen, with the sm2 program ended.
There is no  at the lower right
corner and the only available option at the
top is the at the lower right
corner and the only available option at the
top is the  option.
We need to return to the HOME screen. Therefore, we
press the option.
We need to return to the HOME screen. Therefore, we
press the  key to select that option. Because we
are on the PROGRAM screen, the F5 option takes us back to the HOME screen. key to select that option. Because we
are on the PROGRAM screen, the F5 option takes us back to the HOME screen. |
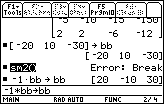
Figure 32
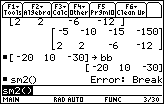
| Figure 32 has us back at the HOME screen. We can see that the former run of the
sm2 program ended in the "Error: Break" condition.
|
Figure 33
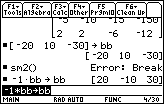
| We need to reverse the values stored in bb.
We do not need to re-enter those values. Instead, we can simply
multiply bb by -1 and store the results in bb.
The keys needed to do this are
 
 
  
 
 .
The calculator multiplies each element of the vector by -1 and stores the
resulting vector in bb, and displays the new bb. .
The calculator multiplies each element of the vector by -1 and stores the
resulting vector in bb, and displays the new bb. |
Figure 34
| Now we need to start the program again. We could re-type the sm2() command,
but we will take this opportunity to demonstrate moving back into the history to retrieve
an earlier command. We use the  key 4 times to move the
highlight up to the sm2() command on the screen, as is shown in Figure 34. key 4 times to move the
highlight up to the sm2() command on the screen, as is shown in Figure 34. |
Figure 35

| Having highlighted the command that we wnat to recall, we press
the  key to actually paste
that command into the command line, shown in Figure 35.
At this point, we could edit tht line if we desired.
Howver, in this case, we simply want to repeat the command
to start the program again. Therefore,
we press key to actually paste
that command into the command line, shown in Figure 35.
At this point, we could edit tht line if we desired.
Howver, in this case, we simply want to repeat the command
to start the program again. Therefore,
we press  to leave Figure 35 and start running the
program in Figure 36. to leave Figure 35 and start running the
program in Figure 36. |
Figure 36

| Again we answer the initial questions of the program. |
Figure 37

| In Figure 37 we supply the name of the Constraint matrix, aa,
and the name of the Function Vector, bb. |
Figure 38

| We again choose to minimize the function. |
Figure 39
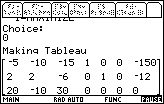
| In Figure 39 we have a new version of the initial TABLEAU.
This time it corresponds exactly with the example on page 239 in the text. |
Figure 40

| We press the  key to move further through the
program, comparing the program output with the values given in the text at each step. key to move further through the
program, comparing the program output with the values given in the text at each step. |
Figure 41
| We press the  key to move further through the
program, comparing the program output with the values given in the text at each step. key to move further through the
program, comparing the program output with the values given in the text at each step. |
Figure 42
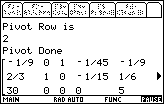
| We press the  key to move further through the
program, comparing the program output with the values given in the text at each step. key to move further through the
program, comparing the program output with the values given in the text at each step. |
Figure 43

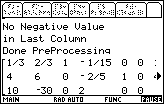
| The program announces, in Figure 43, that we are done, and it redisplays the
matrix. |
Figure 44

| The program now steps through what it believes to be the solution. In Figure
44 we have the statement that x2 is 8. |
Figure 45

| Figure 45 has x3 being 4 2/3, or 14/3 |
Figure 46

| And, Figure 46 shows the objective value to be 60. |
Figure 47

| A final display of the matrix shows up in Figure 47. The program is still running. It is
just PAUSED. Therefore we can use the cursor key to move around in the matrix. |
Figure 48
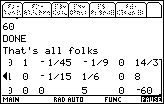
| In fact, we use the  key to move to the right side of
the matrix in Figure 48. key to move to the right side of
the matrix in Figure 48. |
Figure 49
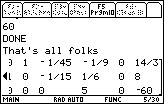
| We press  to allow the program to end, in Figure 49.
This leaves us in the PROGRAM IO screen. to allow the program to end, in Figure 49.
This leaves us in the PROGRAM IO screen. |
Figure 50
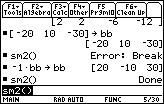
| We return to the HOME screen in Figure 50 by pressing the  key.
Note that the line above the command line indicates that the just finished run of the
sm2 program terminated with the "Done" condition. key.
Note that the line above the command line indicates that the just finished run of the
sm2 program terminated with the "Done" condition. |
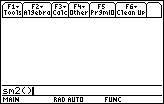





 keys to generate Figure 1. Note that the name of the program, sm2, must be followed by the set
of parentheses.
Now press the
keys to generate Figure 1. Note that the name of the program, sm2, must be followed by the set
of parentheses.
Now press the  key to actually start the program.
key to actually start the program.

 . Then
the program asks for the number of constraints. Our problem has 3 constraints.
Therefore, press
. Then
the program asks for the number of constraints. Our problem has 3 constraints.
Therefore, press  . This should leave the screen as in FIgure 2.
. This should leave the screen as in FIgure 2.
 to accept the number of constraints.
Now the program asks for the constraints in matrix form. Figure 3 has our response
to this request, entered via the bracket notation for a matrix. Read the material immediately below
this table to understand the origin of that matrix.
to accept the number of constraints.
Now the program asks for the constraints in matrix form. Figure 3 has our response
to this request, entered via the bracket notation for a matrix. Read the material immediately below
this table to understand the origin of that matrix.











 , to move over on the display.
Comparing Figure 8 with Figure 7 we can see the values that were cut off in Figure 7.
, to move over on the display.
Comparing Figure 8 with Figure 7 we can see the values that were cut off in Figure 7.


 , and the
, and the  key to move back to the upper left corner of the matrix.
key to move back to the upper left corner of the matrix.










 key. Figure 21 shows that HOME screen with
The sm2() program marked as done, and with the sm2() item pre-loaded in the
command line.
key. Figure 21 shows that HOME screen with
The sm2() program marked as done, and with the sm2() item pre-loaded in the
command line. 
 produce the command line shown in Figure 22. We stop here only to demonstrate
that as we add more to the input line, in Figure 23, part of the command
line scrolls off the left end as new characters are added to the right.
produce the command line shown in Figure 22. We stop here only to demonstrate
that as we add more to the input line, in Figure 23, part of the command
line scrolls off the left end as new characters are added to the right.

 key followed by
the desired name. In the example shown in Figure 23, that name is aa, and was created via the
key followed by
the desired name. In the example shown in Figure 23, that name is aa, and was created via the


 key to accept the command causes the
display to change to that shown in Figure 24.
key to accept the command causes the
display to change to that shown in Figure 24. 





 key.
The calculator responds with Figure 30. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the CANCEL menu item.
To do this we press the
key.
The calculator responds with Figure 30. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the CANCEL menu item.
To do this we press the  key.
key. 



















 key.
Note that the line above the command line indicates that the just finished run of the
sm2 program terminated with the "Done" condition.
key.
Note that the line above the command line indicates that the just finished run of the
sm2 program terminated with the "Done" condition.