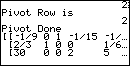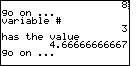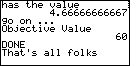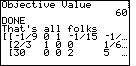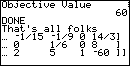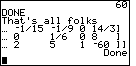Figure 1 (TI-85 Memory Check)

|
Before we even begin to use the SM2 program on the TI-85,
and perhaps even before we load the SM2 program onto the TI-85,
we need to make sure that there is sufficient space for the
program and the storage it requires. To do this we look at
the memory status of the TI-85. The keystrokes 
 Open the window shown in Figure 1. Open the window shown in Figure 1.
|
Figure 2 (TI-85 Memory Check)
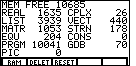
| The first thing that we need to do is to see the current Random Access Memory (RAM)
allocations. To do this, from Figure 1, press the  key.
This will display a version of Figure 2. key.
This will display a version of Figure 2.
Note that the values in Figure 2 are from a particular calculator at a particular time;
they will be different from the values on your calculator screen.
In Figure 2 we see, for example, that we have 10,685 free cells, that we have used 3939 cells
to store LISTs, and that we have used 10,041 cells to store programs. The 10,685 free cells
are quite enough for us. However, let us take this opportunity to examine and possibly
remove an old program to create more open space.
|
Figure 3 (TI-85 Memory Check)

| We leave Figure 2 by pressing the  key to select the DELET option from the menu. The result is shown in Figure 3.
key to select the DELET option from the menu. The result is shown in Figure 3.
Now we need to decide what kinds of things we want to delete.
We want to examine, and possibly delete, a program, but programs are
not listed in the menu shown in Figure 3.
|
Figure 4 (TI-85 Memory Check)

| We press the  key to show additional commands in
the menu option line. This results in Figure 4. Now the fifth option is PRGM.
This is the option we want, so we press the key to show additional commands in
the menu option line. This results in Figure 4. Now the fifth option is PRGM.
This is the option we want, so we press the  key to move to
Figure 5. key to move to
Figure 5. |
Figure 5 (TI-85 Memory Check)
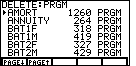
| Figure 5 displays the start of the list of programs that are installed on this calculator.
each program is listed along with the size of the program. A small arrow, at the left of the
screen, points to one program. In Figure 5, that arrow is pointing to the
AMORT program. Extreme care should be taken here. The selected program
will be deleted if the ENTER key is pressed. The cursor keys can be used
to move the
selection arrow tro another program. And the first two function keys, F1 and F2,
can be used to move the display a page at a time.
We will press the  key to move down to the
next page of the display, shown in Figure 6. key to move down to the
next page of the display, shown in Figure 6. |
Figure 6 (TI-85 Memory Check)
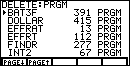
| Figure 6 shows more of the programs currently installed on this calculator.
Note the size of the programs. The smallest program, EFFRAT, takes all of 13
locations. The largest one on Figure 6 is DOLLAR, taking 415 locations.
A review of these programs does not indicated any particular one that we would want to
eliminate. Therefore, we press  to move to
yet another page of the display, in Figure 7. to move to
yet another page of the display, in Figure 7. |
Figure 7 (TI-85 Memory Check)
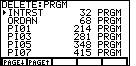
| Here we have more programs, but none that we want to eliminate.
Press  to move to the last programs, shown in Figure 8. to move to the last programs, shown in Figure 8. |
Figure 8 (TI-85 Memory Check)
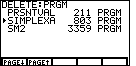
| The final programs on this calculator appear in Figure 8. The selection
arrow, at the extreme left of the screen, was pointing to the PRSNTVAL program,
which we want to keep. The next program, SIMPLEXA, taking up 803 locations, is not needed. We will
pressed the  key to moved the selection arrow to point to
the SIMPLEXA program. This is the condition shown in Figure 8. key to moved the selection arrow to point to
the SIMPLEXA program. This is the condition shown in Figure 8.
Our next step will be to press the  key to DELETE the
selected program, in this case, SIMPLEXA. This will move us to Figure 9. key to DELETE the
selected program, in this case, SIMPLEXA. This will move us to Figure 9.
|
Figure 9 (TI-85 Memory Check)

| Figure 9 shows the result of DELETING the SIMPLEXA program. It has disappeared
from the list and from the calculator. It can not be retrieved.
|
Figure 10 (TI-85 Memory Check)
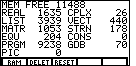
| We leave Figure 9 via the  key. This will return
us to the normal calculator screen. However, we will press the key. This will return
us to the normal calculator screen. However, we will press the
  keys to re-examine the memory
status, and then press keys to re-examine the memory
status, and then press  to display the RAM allocations.
The Figure 10 display can be compared to the Figure 2 display. PRGM memory has decreased
from 10,041 to 9,238 and the FREE memory has increased from 10,685 to 11,488.
We conclude our memory inspection by pressing the to display the RAM allocations.
The Figure 10 display can be compared to the Figure 2 display. PRGM memory has decreased
from 10,041 to 9,238 and the FREE memory has increased from 10,685 to 11,488.
We conclude our memory inspection by pressing the  key
to return to the normal calculator screen. key
to return to the normal calculator screen. |
The problem that we will solve on the calculator is taken from page 233 of the text.
We need to give the program the constraints in matrix form. We can do this in two different ways.
First, we can merely type the matrix using the "[" and "]" characters. This is the
method that we will use immediately below. Second, if we had stored the matrix
earlier under a name, then we could just enter the name. We will use that method for the
second problem, starting in Figure 30.
Right now, we need to remember how to create the augmented matrix for the constraints.
To do this we will re-write the constraints with each variable represented in the
inequality. (Note: we are not adding the "slack variables" here; the program will
do that for us. We are just making sure that each variable appears in each inequaltiy.]
Figure 13

| For Figure 13, we enter the constraints as a matrix via the keys
 
 
 

 
 
  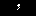
  

 
 
  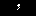
  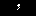
  

 
 
|
Figure 14

| We complete Figure 13 by pressing the  key.
The program now asks for the "Objective Function Vector".
A vector is somewhat like a list, but it has different operations and
properties from a list. On the calculator, a vector is created using
the square braces. For our problem, that objective function vector is
made up of the objective function coefficients. Since our objective function is
z = 1x1 + 1x2
the vector would be [1,1]. We enter this via the keys key.
The program now asks for the "Objective Function Vector".
A vector is somewhat like a list, but it has different operations and
properties from a list. On the calculator, a vector is created using
the square braces. For our problem, that objective function vector is
made up of the objective function coefficients. Since our objective function is
z = 1x1 + 1x2
the vector would be [1,1]. We enter this via the keys
 
 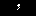

  .
This produces the text seen in Figure 14. .
This produces the text seen in Figure 14.
|
Figure 15

|
Pressing  to accept the
objective function vector of Figure 14 produces the
minimize vs. MAXIMIZE choice. We select the MAXIMIZE
option by pressing the to accept the
objective function vector of Figure 14 produces the
minimize vs. MAXIMIZE choice. We select the MAXIMIZE
option by pressing the  key to complete Figure 15. key to complete Figure 15.
|
Figure 16
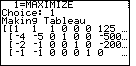
| After Figure 15 we have given the program all of the data
that it needs to do the problem. We press the  key to start the process. Along the way the calculator will display intermediate results.
At times it will pause to let us read those results. The first pause is shown in
Figure 16. Here, the calculator has created the TABLEAU and is displaying it
for us. Note that the entire matrix does not fit on the page. The three dots (...)
at the right side of lines indicates that there is more to be displayed.
key to start the process. Along the way the calculator will display intermediate results.
At times it will pause to let us read those results. The first pause is shown in
Figure 16. Here, the calculator has created the TABLEAU and is displaying it
for us. Note that the entire matrix does not fit on the page. The three dots (...)
at the right side of lines indicates that there is more to be displayed. |
Figure 17
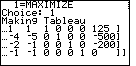
| We have moved from Figure 16 to Figure 17 by pressing the
right cursor key,  , to move over on the display.
The resulting TABLEAU should be compared to the one in the text at
the top of page 234. , to move over on the display.
The resulting TABLEAU should be compared to the one in the text at
the top of page 234. |
Figure 18
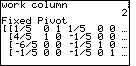
| The calculator was paused at Figure 17 to allow us to examine the TABLEAU.
We did so, and then we press the  key to continue the
program. The calculator entered the "Preprocessing" phase of the algorithm.
In that phase, the calcualtor identified the second row as the work row (not shown), and
within that second row, it identified the second column as the work column.
That means that the value that was in row 2 column 2, namely -5, becomes a
pivot point. Therefore, we use the second elementary row operation to
change it to a 1, and the third elementary
row operation to convert all remaining elements in the second column to be 0.
The calculator has done exactly that, and it has paused at that point to
display the resulting matrix, shown in Figure 18. This matrix corresponds
to the one in the middle of page 234 in the text. key to continue the
program. The calculator entered the "Preprocessing" phase of the algorithm.
In that phase, the calcualtor identified the second row as the work row (not shown), and
within that second row, it identified the second column as the work column.
That means that the value that was in row 2 column 2, namely -5, becomes a
pivot point. Therefore, we use the second elementary row operation to
change it to a 1, and the third elementary
row operation to convert all remaining elements in the second column to be 0.
The calculator has done exactly that, and it has paused at that point to
display the resulting matrix, shown in Figure 18. This matrix corresponds
to the one in the middle of page 234 in the text. |
Figure 19
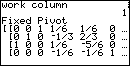
| We leave Figure 18 by pressing the  key
to continue the program. The calculator continues the preprocessing
phase, identifying the third row and first column as the work row and column.
It then changes the pivot point to a 1, and converts the remaining work column
values to 0. Again, we pause to examine the matrix, shown in Figure 19.
This matrix corresponds to the bottom matrix on page 234. key
to continue the program. The calculator continues the preprocessing
phase, identifying the third row and first column as the work row and column.
It then changes the pivot point to a 1, and converts the remaining work column
values to 0. Again, we pause to examine the matrix, shown in Figure 19.
This matrix corresponds to the bottom matrix on page 234.
|
Figure 20

| The  key continues the process. The program
looks at the matrix and determines that we are done with the preprocessing
phase. It indicates that fact in the message on Figure 20,
and it displays the same matrix again. key continues the process. The program
looks at the matrix and determines that we are done with the preprocessing
phase. It indicates that fact in the message on Figure 20,
and it displays the same matrix again. |
Figure 21
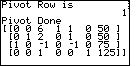
| The  key leaves Figure 20 and moves the
calculator into the basic algorithm. Here the calculator determines that the
fourth column is the work column, and that the first row is the work row.
The calculator makes the element in row 1 column 4 become 1 and the calculator
uses that 1 to change the other elements in that column to be 0.
Once this is done, the calculator displays the resulting matrix and pauses
to allow us to examine it, as shown in Figure 21. key leaves Figure 20 and moves the
calculator into the basic algorithm. Here the calculator determines that the
fourth column is the work column, and that the first row is the work row.
The calculator makes the element in row 1 column 4 become 1 and the calculator
uses that 1 to change the other elements in that column to be 0.
Once this is done, the calculator displays the resulting matrix and pauses
to allow us to examine it, as shown in Figure 21. |
Figure 22
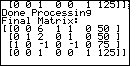
| Pressing the  key continues the algorithm.
The calculator determines that we are done. It gives the message that the final
matrix is being displayed and it pauses as in Figure 22. key continues the algorithm.
The calculator determines that we are done. It gives the message that the final
matrix is being displayed and it pauses as in Figure 22. |
Figure 23

| Now we can get the calculator's best guess at the results by pressing the
 key. The program responds by indicating that the
maximum value for the objective function can be
found when x1 has the value 75.
This is exactly the value presented in the second sentence of the paragraph at the bottom
of page 234. The other values follow in Figures 24 and 25, with the value of the
objective function being given in Figure 26. key. The program responds by indicating that the
maximum value for the objective function can be
found when x1 has the value 75.
This is exactly the value presented in the second sentence of the paragraph at the bottom
of page 234. The other values follow in Figures 24 and 25, with the value of the
objective function being given in Figure 26.
|
Figure 24

| We continue by pressing the  key,
to find, in Figure 24, that the
value of x2 needs to be 50. key,
to find, in Figure 24, that the
value of x2 needs to be 50. |
Figure 25

| Another  key shows us Figure 25, whcih gives us
s2, the second slack variable, having the value 50. key shows us Figure 25, whcih gives us
s2, the second slack variable, having the value 50. |
Figure 26

| Yet another  key moves us to Figure 26, which repeats
that the objective function value will be 125. key moves us to Figure 26, which repeats
that the objective function value will be 125. |
Figure 27
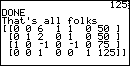
| For a convenience, the program continues, after a press of the
 key, to redisplay the matrix, as shown in Figure 27.
The program is paused at that point so that we can scroll over on the matirx if need be.
In this case the entire matrix is displayed on screen so we do not need to scroll
at all. key, to redisplay the matrix, as shown in Figure 27.
The program is paused at that point so that we can scroll over on the matirx if need be.
In this case the entire matrix is displayed on screen so we do not need to scroll
at all. |
Figure 28
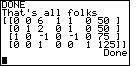
| And, finally, another  key sends the program to
its end. This leaves the screen as in Figure 28. key sends the program to
its end. This leaves the screen as in Figure 28. |
One of the problems with the approach shown above is that
there is no asy recovery if you have made an error
in the original matrix, or in the objective function vector.
The program merely continues, and probably produces the wrong answers.
It is much safer for us to store the constraint matrix and the objective vector on
the calculator before we use SM2. That way, if an error is found, we can correct it
and rerun the program without having to re-enter all of the coefficients and constants.
We will demonstrate this in the remaining Figures.
The next example is taken from page 238 of the text. In this case there are three
variables and two constraints. The problem is stated as:
Figure 29
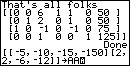
| The first step is to create the constraint matrix. The key strokes
 
 
  

 
 
 

 
  enters the matrix. To
save it under a name we use the enters the matrix. To
save it under a name we use the  key followed by
the desired name. In the example shown in Figure 29, that name is AA and was created via the key followed by
the desired name. In the example shown in Figure 29, that name is AA and was created via the
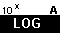  key sequence. key sequence.
|
Figure 30

| Press the  key to accept the matrix of Figure 29. In Figure 30
we will enter the objective vector and save it under the name BB.
A small warning: this is not the right set of values, but we will enter them here,
use them, discover our error, correct them, and rerun the program with the correct
values. The keys key to accept the matrix of Figure 29. In Figure 30
we will enter the objective vector and save it under the name BB.
A small warning: this is not the right set of values, but we will enter them here,
use them, discover our error, correct them, and rerun the program with the correct
values. The keys
 
  
  produce the
vector. Note the single left and right square bracket. Then we
store the vector in BB via the keys produce the
vector. Note the single left and right square bracket. Then we
store the vector in BB via the keys

  and and  .
We finish Figure 30 by typing the name of the program, using the key sequence: .
We finish Figure 30 by typing the name of the program, using the key sequence:
 
 
 . .
|
Figure 31

| The program starts as before, asking for the number of variables,
  ,
the number of constraints, ,
the number of constraints,
  ,
and then the matrix of constraint coefficients and constants. In this case,
we have already entered that matrix and we have saved it under the name
AA. Therefore, we type the name of the matrix via the ,
and then the matrix of constraint coefficients and constants. In this case,
we have already entered that matrix and we have saved it under the name
AA. Therefore, we type the name of the matrix via the
 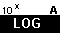 keys. After
that we should have a display identical to Figure 31. keys. After
that we should have a display identical to Figure 31.
|
Figure 32

| We leave Figure 31 by pressing  .
The program asks for the Objective Function Vector.
Again, we have entered this and saved it under the name BB.
Therefore, press .
The program asks for the Objective Function Vector.
Again, we have entered this and saved it under the name BB.
Therefore, press  
  and and
 . The program moves on to ask if we want
to minimize or maximize? We respond with . The program moves on to ask if we want
to minimize or maximize? We respond with  for minimize.
All of this should produce Figure 32. for minimize.
All of this should produce Figure 32.
|
Figure 33
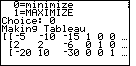
| We press  to start the process.
The program creates the TABLEAU and displays it, as in Figure 33. We can
compare this to the matrix on page 239. It is almost the same. However,
we note that the signs on the values in the bottom row are reversed. What happened? to start the process.
The program creates the TABLEAU and displays it, as in Figure 33. We can
compare this to the matrix on page 239. It is almost the same. However,
we note that the signs on the values in the bottom row are reversed. What happened?
If we go back we will find that we created the objective function vector
using the equation
Z = -20x1 + 10x2 - 30x3
We created Z = -z as was done in the book. However, the program, SM2,
does this for us when we select the "minimize" option. Therefore, SM2
has undone our conversion, and the values in the final row of the TABLEAU have the wrong sign.
We need to stop the program, change the vector and then run the program again with the
new vector.
|
Figure 34

| We stop the program by pressing the  key.
The calculator responds with Figure 34. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the QUIT menu item.
To do this we press the key.
The calculator responds with Figure 34. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the QUIT menu item.
To do this we press the  key. key. |
Figure 35
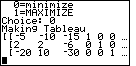
| Figure 35 demonstrates that we are out of the program and
back to the normal calculator screen. |
Figure 36
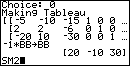
| In the middle of Figure 36 you can see the steps taken to reverse the signs
on the values stored in BB. Namely, we multiply -1 times BB and store the result in BB.
The keys needed to do this are
  
 
 
  
 .
The calculator multiplies each element of the vector by -1 and stores the
resulting vector in BB, and displays the new BB. Now all we need to do is to
start the program again. We use the .
The calculator multiplies each element of the vector by -1 and stores the
resulting vector in BB, and displays the new BB. Now all we need to do is to
start the program again. We use the
 
 
 keys to generate SM2 to complete Figure 36. keys to generate SM2 to complete Figure 36.
|
Figure 37

| The program restarts. We answer the questions again. |
Figure 38

| Figure 38 shows more answers. |
Figure 39
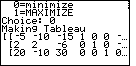
| With Figure 39 we have returned to the spot where we found our original error.
Now we look at the initial TABLEAU and verify that it has exactly the values
that we expect. |
Figure 40

| The  key moves us to Figure 40, which shows the
matrix after having made row 1 column 3 the pivot element. The matrix now checks with the
one in the middle of page 239. key moves us to Figure 40, which shows the
matrix after having made row 1 column 3 the pivot element. The matrix now checks with the
one in the middle of page 239. |
Figure 41

| In Figure 41 we find that the program has determined that we are done
with the preprocessing. |
Figure 42
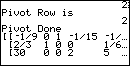
| Figure 42 shows the matrix after the next step. It now corresponds to the
matrix at the bottom of page 239. |
Figure 43

| The program announces, in Figure 43, that we are done, and it redisplays the
matrix. |
Figure 44

| Figure 44 continues the display from Figure 44, except that we use the
 key a number of times so that we can see the
right side of the matrix. key a number of times so that we can see the
right side of the matrix. |
Figure 45

| The program now steps through what it believes to be the solution. In Figure
45 we have the statement that x2 is 8. |
Figure 46
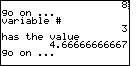
| Figure 46 has x3 being 4 2/3, or 14/3. |
Figure 47
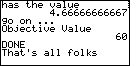
| And, Figure 47 shows the objective value to be 60. |
Figure 48
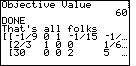
| A final display of the matrix shows up in Figure 48. The program is still running. It is
just PAUSED. Therefore we can use the cursor key to move around in the matrix. |
Figure 49
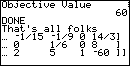
| Here, in Figure 49, we have moved again to the right side of the matrix. |
Figure 50
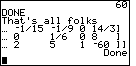
| One last  key finishes off the program and returns us to the
normal calculator mode. key finishes off the program and returns us to the
normal calculator mode. |


 Open the window shown in Figure 1.
Open the window shown in Figure 1.

 key.
This will display a version of Figure 2.
key.
This will display a version of Figure 2. 
 key to select the DELET option from the menu. The result is shown in Figure 3.
key to select the DELET option from the menu. The result is shown in Figure 3.

 key to show additional commands in
the menu option line. This results in Figure 4. Now the fifth option is PRGM.
This is the option we want, so we press the
key to show additional commands in
the menu option line. This results in Figure 4. Now the fifth option is PRGM.
This is the option we want, so we press the  key to move to
Figure 5.
key to move to
Figure 5. 
 key to move down to the
next page of the display, shown in Figure 6.
key to move down to the
next page of the display, shown in Figure 6. 
 to move to
yet another page of the display, in Figure 7.
to move to
yet another page of the display, in Figure 7. 
 to move to the last programs, shown in Figure 8.
to move to the last programs, shown in Figure 8. 
 key to moved the selection arrow to point to
the SIMPLEXA program. This is the condition shown in Figure 8.
key to moved the selection arrow to point to
the SIMPLEXA program. This is the condition shown in Figure 8.  key to DELETE the
selected program, in this case, SIMPLEXA. This will move us to Figure 9.
key to DELETE the
selected program, in this case, SIMPLEXA. This will move us to Figure 9.


 key. This will return
us to the normal calculator screen. However, we will press the
key. This will return
us to the normal calculator screen. However, we will press the

 keys to re-examine the memory
status, and then press
keys to re-examine the memory
status, and then press  to display the RAM allocations.
The Figure 10 display can be compared to the Figure 2 display. PRGM memory has decreased
from 10,041 to 9,238 and the FREE memory has increased from 10,685 to 11,488.
We conclude our memory inspection by pressing the
to display the RAM allocations.
The Figure 10 display can be compared to the Figure 2 display. PRGM memory has decreased
from 10,041 to 9,238 and the FREE memory has increased from 10,685 to 11,488.
We conclude our memory inspection by pressing the  key
to return to the normal calculator screen.
key
to return to the normal calculator screen. 



 keys to generate Figure 11.
Now press the
keys to generate Figure 11.
Now press the  key to actually start the program.
key to actually start the program.















 , to move over on the display.
The resulting TABLEAU should be compared to the one in the text at
the top of page 234.
, to move over on the display.
The resulting TABLEAU should be compared to the one in the text at
the top of page 234. 


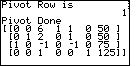





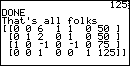
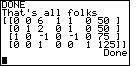
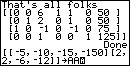

 key followed by
the desired name. In the example shown in Figure 29, that name is AA and was created via the
key followed by
the desired name. In the example shown in Figure 29, that name is AA and was created via the






 key.
The calculator responds with Figure 34. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the QUIT menu item.
To do this we press the
key.
The calculator responds with Figure 34. We know what we need to do, and that does not
involve changing the program. Therefore, we want to select the QUIT menu item.
To do this we press the