Finding the Inverse of a square matrix

This page is devoted to presenting, in a step by step fashion, the keystrokes and the screen images for finding the inverse of a square matrix on a TI-83. The square matrix used is

This particular matrix was chosen because its inverse is in fact a matrix of integer values.

Figures 1 through 34 demonstrate using the calculator to perform the elementary row operations on an augmented matrix. Within this pattern, at Figure 24 there is a decision to use some less than obvious steps so that we do not need to use any fractions.
Figures 35 through 37 demonstrate that the resulting portion of the matrix is indeed the inverse of the initial matrix.
Figures 38 returns to the process, essentially picking up the task at Figure 24, but this time uses fractions in some of the subsequent steps. This produces, in Figures 48 and 49, the same answer that we achieved in Figures 33 and 34.
Figure 50 shows the one step process for finding the inverse using the inverse key on the calculator.
Figures 51 through 53 demonstrate the more usual case where, still starting with a matrix of integer values, the inverse matrix has fractional entries.
Figures 54 through 56 demonstrate a matrix that does not have an inverse. In this case we start with a matrix that has a zero as one of the entries. This, by itself, certainly does not cause the matrix to be singluar, i.e., not have an inverse.
Figures 56 and 57 show another singular matrix, this time it is one without a zero entry.

Figure 1	This demonstration starts with a calculator that has no defined matrices. We have used the keystrokes to open the MATRIX window. Then we use the twice to move to the EDIT option. Finally we press to move to edit the highlighted matrix, matrix [A].
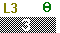Figure 2	Here we have already pressed 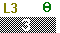to set the dimensions of the matrix so that it has 3 rows and three columns.
Figure 3	In Figure 3 we have entered all of the elements of the desired matrix although we have yet to press the key to accept the final value, namely 5, for the third row third column entry. We move to Figure 4 by pressing the key and then we exit the MATRIX EDIT window by pressing .
Figure 4	Again, this calculator started with nothing on it so we are back at a blank screen. We would like to see the contents of [A] so we will return to the MATRIX window via the keys .
Figure 5	Not to belabor the point, but to get the name of a matrix onto the main screen we need to use the MATRIX menu to select the name of the matrix. The calculator does not recognize [A] as the name of a matrix if we type it as three separate characters. Given that our desired matrix is already highlighted in Figure 5 we need only press to select the name of that matrix.
Figure 6	In FIgure 6 we have the result, the name of [A] pasted ontot he screen. We press to tell the calculator to evaluate the command, which it does and displays in Figure 7.
Figure 7	Here we see the original matrix. Unfortunately for us, the algorithm for determining the inverse of this matrix requires that we start with a matrix that has this as its first three columns and the identity matrix as its last three columns. what we really want is We can use the original matrix and a pair of matrix commands to create this desired matrix.
Figure 8	The first command that we want is the augment( command, found in the MATRIX MATH screen. Press and to get to the screen on Figure 8. The desired command is at the bottom of the screen.
Figure 9	We use the key to move the highlight to the desired command. Then use the key to select that command and paste it to the screen.
Figure 10	The augment( command takes two arguments, both matrices, and it produces a new matrix by "pasting" the two matrices together. We return to the MATRIX menu to select the name [A] from the list of the matrices (Figure 5 has the screen that we would use).
Figure 11	Now, the second argument needs to be a 3x3 identity matrix. We can manufacture such a matrix by using the identity( command. Return to the MATRIX MATH menu to find that command.
Figure 12	Figure 12 shows the MATRIX MATH menu and has the correct function highlighted. Press to past the command onto the main screen.
Figure 13	The command is almost complete. We still need to tell the identity( command the size of the desired identity matrix.
Figure 14	Figure 14 has the completed command. The 3 indicates that we want a 3x3 identity matrix. The first right parenthesis, ), ends the identity( command. The final right parenthesis ends the augment( command.
Figure 15	Pressing the key to perform the command produces the matrix shown in Figure 15. This is the matrix that we want. It is stored in the Ans location. The goal, for the next number of steps, will be to use the elementary row operations to convert the first three columns of the augmented matrix into the identity matrix. There are many ways to do this. In this case we will start the process by swapping the first two rows.
Figure 16	To do this we return to the MATRIX MATH menu, and move down to the rowSwap( command. Then press to select that command.
Figure 17	The syntax of the rowSwap command is to specify the matrrix to use, followed by the numbers of the two rows to use.
Figure 18	We use the key sequence to generate the Ans name, and then follow that by the rest of the command.
Figure 19	The row swap is complete. Now, to generate a 1 in row 1 column 1 we want to multiply row 2 by -1 and add it to row 1. The command to do this is the *row+( command.
Figure 20	Figure 20 is a return to the MATRIX MATH menu were we have moved to highlight the *row+( command.
Figure 21	Press to past the command ontop the screen. The syntax of the *row+( command is to specify the number to use to multiply the row, then the name (location) of the matrix to use, and finally, the numbers of the rows to use.
Figure 22	Figure 22 shows both the completed and the executed command. We now have the desired 1 in row 1 column 1. The next step is to get a 0 in row 2 column 1. We can do this by multiplying -3 times row 1 and adding the result to row 2.
Figure 23	Figure 23 shows the needed command and the result of executing it. Now that there is a 0 in row 2 column 1, the next step is to get a 0 into row 3 column 1. We do that by multiplying -8 times row 1 and adding the result to row 3.
Figure 24	Figure 24 shows the desired command and the result. Our next step is to generate a 1 in row 2 column 2. As before, there are many ways to do that. We will spend the next few steps doing this without generating any fractions. (If you want to do this in a more direct way, using fractions, skip down to Figure 38.) To do this without generating fractions we need to find a multiple of 23, the value in row 2 column 2, and a multiple of 59, the value in row 3 column 2, that are different from each other by 1. We observe (after a lot of examination) that 18*23 is 414 and 7 times 59 is 413. We can use these to get our desired result. First we multiply row 2 by -18 to generate a 414 in row 2 column 2.
Figure 25	The command that we want to use is *row( command. We return to the MATRIX MATH menu to find that command.
Figure 26	The syntax for the *row( command is to give the value used to multiply, the name of the matrix to use, and finally the number of the row to multiply. You can see the completed command and the result of the command in Figure 26.
Figure 27	Having performed the command in Figure 26 we are ready to multiply 7 times row 3 and add it to row 2. Figure 27 shows that command and the result. As you cn see, our objective, to get a 1 in row 2 column 2 has been accomplished. The next stepis to get a 0 into row 3 column 2.
Figure 28	Multiplying row 2 by 59 and adding the result to row 3 generates the desired 0. The next step is to generate a 1 in row 3 column 3. This time we have no choice but to multiply row 3 by 1/18.
Figure 29	The command to multiply row 3 by 1/18 is shown in Figure 29. The result has the desired 1 in row 3 column 3. At this point we have generated 1's down the main diagonal and we have 0's below that diagonal. In the process of generating this situation, we have also generated new values in columns 4, 5, and 6. We can see some of those values in Figure 29, but we might want to examin the rest of the matrix.
Figure 30	To do this we use the key repeatedly to move the display to the right. The result appears in Figure 30.
Figure 31	Our next phase will be to generate 0's above the diagonal, starting in column 3. However, since we already have 1's on the main diagonal, this is a straight forward task. We start by working up column 3. Multiplying 1 times row 3 and adding it to row 2 will generate the desired 0 in row 2 column 3.
Figure 32	Multiplying 9 times row 3 and adding it to row 1 will generate the desired 0 in row 1 column 3.
Figure 33	Having completed column 3, we move back to column 2. Multiplying -8 times row 2 and adding it to row 1 will generate the desired 0 in row 1 column 2. After performing the command, the right side of the matrix holds the desired inverse of the original matrix. In Figure 33 we can only see part of that answer.
Figure 34	To get to Figure 34 we have used the cursor control key to move the display to the right. There is our answer. The inverse matrix is
Figure 35	Unfortunately, there is no easy way to chop apart a matrix the way we assembled on, back in Figures 14 and 15. We will have to re-enter the matrix, this time as [B]. To do this we return to the MATRIX EDIT menu and highlight option 2, [B]. Then press to start the editor for [B].
Figure 36	In Figure 36 we have entered the desired dimensions and values for the inverse matrix. Once wew are done we press to exit the editor.
Figure 37	Figure 37 reflects our construction of *[A][B]** along with the result of pressing the key to perform the multiplication. As you see, the result is indeed the 3x3 identity matrix.
Figure 38	For the sake of completeness, Figures 38 through 49 redo some of the work that we already did, but this time avoiding the strange multiplication that we did in Figure 26. Figure 38 shows the matrix as it existed before that multiplication. Our task, at this point in the proces was to get row 2 colum 2 to be a 1 instead of its current value of -23.
Figure 39	The most straight forward command to do this is to multiply row 2 by -1/23. The command to do this is shown at the bottom of Figure 39. This will work, but it will also generate fractional values which will be displayed as decimal values if we perform the command as written.
Figure 40	We open the MATH menu by pressing the key. The first option is the one we want. Press to paste that option to the end of the command that we started in Figure 39.
Figure 41	Here is the complete comamnd. Press to perform the comamnd and move to the next Figure.
Figure 42	Indeed, we have created the 1 in row 2 column 2, but we have introduced fractions in the rest of row 2.
Figure 43	Figure 43 shows the right sidee of the matrix, displaying more of the fractional values.
Figure 44	Having the 1 in row 2 column 2, the next step is to generate a 0 in row 3 column 2. The command to do this and the result of performing that command is shown in Figure 44.
Figure 45	To convert the -1/23 in row 3 column 3 to a 1, we multiply that row by 23.
Figure 46	To convert the -30/23 in row 2 column 3 to a 0, we multiply row 3 by 30/23 and add the result to row 2.
Figure 47	To convert the -9 in row 1 column 3 to a 0, we multiply row 3 by 9 and add the result to row 1.
Figure 48	To convert the 8 in row 1 column 2 to a 0, we multiply row 2 by -8 and add the result to row 1. Having done all of this we have achieved our goal with teh identity matrix now in columns 1-3 and the inverse in columns 4-6. In Figure 48 we can see just part of the inverse matrix.
Figure 49	For Figure 49 we use the cursor control key to move the display to the right.
Figure 50	As much fun as is the process for finding the inverse, it really is a bit tedious. Fortunately, the calculator is willing to do all of this behind the scenes. If we use the MATRIX menu to paste [A] onto our main screen, and follow that by using the key to generate ^-1 and then put the command to display the result in fractional form after that, then press , the calculator respondes directly with Figure 50 giving the inverse matrix.
Figure 51	All of the work that has been done so far has been on our original matrix. That matrix is a somewhat special case in that its matrix does not have fractional values. A more common case is that when all of the elements in the origianl matrix are integers, then the inverse matrix will contain fractional values. To demonstrate this, Figure 51 returns to the MATRIX EDIT screen to change the value of just one element of our original matrix. Originally, the value in row 1 column 1 was a 3. We have used the editor to change that value to be 4. Press the sequence to exit the editor.
Figure 52	To generate the command on Figure 52 it was enough to recall the last command via the sequence. Then, use the key to perform the command. The result, shown in Figure 52 has many fractional values in the inverse.
Figure 53	Figure 53 merely shows the rest of the inverse from Figure 52.
Figure 54	Finding the inverse is not always so easy. In Figure 54 we have created a new matrix, this time stored in [D].
Figure 55	Here we have displayed the matrix and formulated the command to find the inverse matrix. Press the to move to Figure 56.
Figure 56	Figure 56 shows that there is an error here. The error is designated as SINGULAR MAT. This means that there is no inverse. We have the same situation with numbers, namely that there is no inverse for the number 0. With matrices, however, it is possible for a matrix such as [D] that is not the zero matrix to still not have an inverse.
Figure 57	We conclude this page by showing yet another matrix, this one not having any 0 in it, that has no inverse.
Figure 58	Indeed, the calculator reports that our matrix [E] is SINGULAR, and therefore has no inverse.