Solving for Linear Equations

Here is a list of the various types of questions that ask you to deerive a linear equation:
  1. You are given the slope and the y-intercept, find the equation of the line;
  2. You are given the slope and a point on the line, but not the intercept, find the equation of the line;
  3. You are given two points on the line, find the equation of the line;
  4. You are told that the line is horizontal and given a point on the line, find the equation of the line;
  5. You are told that the line is vertical and given a point on the line, find the equation of the line;
  6. You are told that the line is parallel to a line given in slope-intercept form, and that the new line contains a point, find the equation of the line;
  7. You are told that the line is perpendicular to a line given in slope-intercept form and that the line contains a point, find the equation of the line;
  8. You are told that the line is parallel to a line given in standard form and that the new line contains a point, find the equation of the line;
  9. You are told that the line is perpendicular to a line given in standard form and that the new line contains a point, find the equation of the line.
Many of these become quite mechanical solutions, some to the point of just writing out the answer, others lending themselves to a straight forward program of steps.

Now we will repeat the list but with a discussion of how to go about solving such a problem.
1. You are given the slope and the y-intercept, find the equation of the line
 Since we know the slope-intercept form of a linear equation looks like y = mx + b, where m is the slope and b is the second coordinate of the y-intercept, we have been given everything that we need to just write the equation. We just plug in the given values. So, if we are given that the slope is 2/3 and the y-intercept is (0,6) then the equation is y=(2/3)x + 6.
2. You are given the slope and a point on the line, but not the intercept, find the equation of the line
 Knowing the slope but not the y-intercept means tht we could write a portion of the desired equation, but not all of it. We start with the slopeintercept form of the equation, y = mx + b, and we substitute the given value of the slope for m. So, if we are given that the slope is (-3/4) and that the line contains the point (8,1), then we know that we could at least write the equation as y = (-3/4)x + b. The other piece of information is that the point (8,1) is on the line. But that means that the values x=8 and y=1 must make the equation work. Replacing x and y in the equation
y = (-3/4)x + b
with 8 and 1 respectively we now have the equation
1 = (-3/4)8 + b
but this is an equation in one variable, b and we can solve for that variable:
1 = -6 + b
7 = b
which means that we now know the second coorcinate of the y-intercept and the problem has become identical to the first one; we can just write the answer
y = (-3/4)x + 7
3. You are given two points on the line, find the equation of the line
 In this case we are not given the slope and we are not given the y-intercept. However, if we have two points, we can find the slope of the line between them. The slope between points (x1,y1) and (x2,y2) is defined as
  y2 - y1
slope = m =   
 x2 - x1
This means that we can compute the slope and therefore change this problem into the one we solved above. The steps are
  1. look at the coorcdinates of the two points
  2. figure out the numberator and the denominator of the fraction that is the slope
  3. if the denominator is zero, then this is a vertical line and the equation will be of the form 1x+0y=C, where C is the x-coordinate of either point that we are given (the two points must have the same x-coordinate if the denominator, x2 - x1 is zero). And, in this case, wqe are done.
  4. IF the denominator is not zero then we can reduce the fraction that is the slope by dividing the numerator and the denominator by the greatest common factor of the numerator and the denominator.
  5. now we have the slope and we can take either of the two given points, substitute the slope for m and the coordinates of that point for x and y in the equation y = mx + b and solve for b. After that, we know the slope m and the value of b which means that we can write the equation using those values.

The process becomes so straight forward that we can write a program to do this. Such a program, slope.83p for the TI-83 family, is given below.

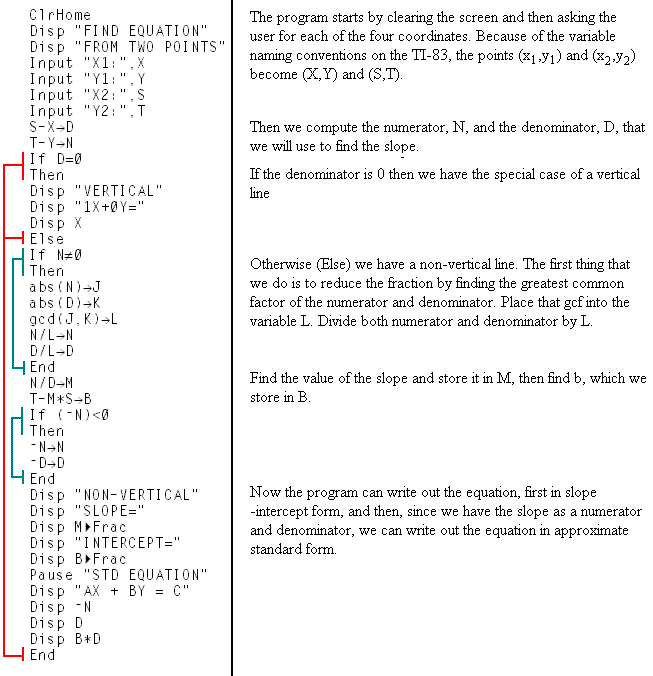A sample run of the program follows, finding the equation of the line through the two points (5,9) and (7,-1).
Screen 1
 Move to the program listing by pressing the key. Then use the arrow keys to move down the list to select (highlight) the SLOPE program. To leave this screen, press the key.
Screen 2
 Start the program by pressing the key.
Screen 3
 The program asks for each of the coordinates of the two points. Be sure to enter them in the correct order. Here the calculator has been given the points (5,9) and (7,-1). Press the key after each coordinate value.
Screen 4
 The program calculates and displays the SLOPE (in this case -5) and the second coordinate of the Y-INTERCEPT, in this case 34. Thus, the slope-intercept form of the equation would be
y = -5x + 34
The program then goes into a "pause" mode, indicated by the line of dots in the upper right corner of the screen. This gives you a chance to read the screen before more information is displayed Press the key to continue.
Screen 5
 The program now displays the calculated values of A, B, and C in the standard form Ax + By = C. In this case that would be 5x + 1y = 34

The program is pretty good, though the output is a bit unpleasant. It is slightly more difficult to obtain nicer looking output on the TI-83 family of calculators. If your calculator has the program TOSTR on it then the program SLOPE1, listed below in three parts, produces better output.

Part 1Part 2Part 3

A comparison of the two programs will show that the SLOPE1 program is merely an extension of the SLOPE program with the added lines merely making the output nicer. A sample run of the SLOPE1 program follows:

Screen 1
 Move to the program listing by pressing the key. Then use the arrow keys to move down the list to select (highlight) the SLOPE1 program. To leave this screen, press the key.
Screen 2
 Start the program by pressing the key.
Screen 3
 The program asks for each of the coordinates of the two points. Be sure to enter them in the correct order. Here the calculator has been given the points (5,9) and (7,-1). Press the key after each coordinate value.
Screen 4
 The program calculates and displays the SLOPE (in this case -5) and the second coordinate of the Y-INTERCEPT, in this case 34. In this program the general slope-intercept form is given, Y=MX+B, and that is followed by the actual equation:
y = -5x + 34
The program then goes into a "pause" mode, indicated by the line of dots in the upper right corner of the screen. This gives you a chance to read the screen before more information is displayed Press the key to continue.
Screen 5
 The program now displays the standard form Ax + By = C and follows that with the desired equation 5x + 1y = 34 in standard form.
4. You are told that the line is horizontal and given a point on the line, find the equation of the line
 A horizontal line ahas a slope of 0 so the slope-intercept equation becomes y = 0x + +b which we can simplify to y = b. The value of b has to be the same value as the second coordinate of the given point. [If it were not the smae then the slope between the y-intercept and the given point could not be 0.] Therefore, we can use that second coordinate in place of the constant b and just write the equation. Thus, the equation of the horizontal line through (5,7) must be y = 7.
5. You are told that the line is vertical and given a point on the line, find the equation of the line
  Vertical lines have undefined slope. In this case, the first coordinate of everypoint on the line is some constant value. If we are given a point on the line then the first coordinate of that point is the value of x that defines the line. We can write the equation in standard form as x 0y = C where C is the first coordinate of the given point. [We make the coefficient of y be 0 so that the value of the y-coordinate for any point is immaterial to the equation. Also, note that since the slope is undefined, we cannot write the equation in slope-intercept form.] Thus, the equation of the vertical line through (5,7) must be x = 5.
6. You are told that the line is parallel to a line given in slope-intercept form, and that the new line contains a point, find the equation of the line
 This is just a wordy version of an earlier problem. Parallel lines have the same slope. We are given the slope-intercept form of a line, therefore must be given the desired slope for our new line. Thus, we know the slope and a point on the line, a problem we already addressed.

To find the equation of a line parallel to y=(-2/3)x + 8 and that contains the point (-6,5) we really want to find the equation of a line with slope (-2/3) and containing the point (-6,5). As before, the slope intercept form of the answer can be partially filed out as y = (-2/3)x + b. We know that (-6,5) must make the equation valid. Substituting -6 for x and 5 for y we get 5 = (-2/3)(-6) + b which simplifies to 5 = 4 + b and that becomes 1 = b. Finally, we fill out the slope-intercept form with the the known values and have y = (-2/3)x + 1.

7. You are told that the line is perpendicular to a line given in slope-intercept form and that the line contains a point, find the equation of the line
  With the exception of horizontal and vertical lines, two lines are perpendicula if and only if the product of their slopes is -1. This means that a line with slope (3/5) is perpendicular to a line with slope (-5/3). Thus, given a slope-intercept equation for a line we can find the slope of that line and from that value we compute its negative reciprocal which becomes the slope of our new line. And, again, we have changed this problem into an earlier one since we now know the slope of the line and a point on the line.

For example, to find the equation of a line that is perpendicular to the line y = (3/5)x + 7 and contains the point (-9,-7) we know that we want to find the equation of a line with slope (-5/3) and containing (-9,-7). The partially completed slope-intercept form of the answer will be y = (-5/3)x + b. We know that (-9,-7) must make the equation valid. Substituting -9 for x and -7 for y we get -7 = (-5/3)(-9) + b which simplifies to -7 = 15 + b and that becomes -22 = b. Finally, we fill out the slope-intercept form with the the known values and have y = (-5/3)x - 22.

8. You are told that the line is parallel to a line given in standard form and that the new line contains a point, find the equation of the line
 A short answer to this kind of problem is to change the standard form of the given equation into slope-intercept form, thus changing the problem into one we have examined already. That will work! However, if we do this using the standard form we see that:
Ax + By = C
By = (-A)x + C
y = (-A/B)x + (C/B).
In particular, the slope is completely determined by the values of A and B. Therefore, a new line that is parallel to the given line will have the same slope, which means that A and B will be the same for the new line. All we have to do is to find C. The one extra piece of information is that some point is on the new line. But that means that the equation of the new line must work if we substitute the coordinates of the new point for x and y in the equation. From that we can find the value of C.

For example, to find the equation of a line that is parallel to 3x + 7y = -12 and that goes through (4,5) we know that the answer will look like 3x + 7y = C, and we know that we can substitute 4 for x and 5 for y. This gives us 3(4) + 7(5) = C, but that simplifies to 12 + 35 = C which resolves to 47 = C. Therefore, the desired answer is 3x + 7y = 47.

9. You are told that the line is perpendicular to a line given in standard form and that the new line contains a point, find the equation of the line
 Just as in the previous section, a short answer to this kind of problem is to change the standard form of the given equation into slope-intercept form, thus changing the problem into one we have examined already. That will work! However, if we do this using the standard form we see that:
Ax + By = C
By = (-A)x + C
y = (-A/B)x + (C/B).
In particular, the slope is completely determined by the values of A and B. Therefore, a new line that is perpendicular to the given line will have a slope which is the negative reciprocal of (-A/B), which means that A and B will swap places for the new line and we need to change the sign of one of them. All we have to do is to find C. The one extra piece of information is that some point is on the new line. But that means that the equation of the new line must work if we substitute the coordinates of the new point for x and y in the equation. From that we can find the value of C.

For example, to find the equation of a line that is perpendicular to 3x + 7y = -12 and that goes through (4,5) we know that the answer will look like 7x - 3y = C, and we know that we can substitute 4 for x and 5 for y. This gives us 7(4) - 3(5) = C, but that simplifies to 28 - 15 = C which resolves to 13 = C. Therefore, the desired answer is 7x - 3y = 13.

©Roger M. Palay
Saline, MI 48176
August, 2010