In order to tie comments to specific locations in the book, I have used the available page ruler sheet to
identify lines in the text. A copy of that page ruler sheet can be printed from
The Index Sheet. Even so, the line numbers are approximate and depend on
everything from the printer you use to the way you position the index sheet.
Still, this is better than saying top, middle, or bottom of the page.
Chapter 0: Precalculus Review |
| 0.1 Real numbers |
| Page | Line # | Notes |
| 2 | 12 |
Although it is nice to just jump into the real numbers, it
is better to start with
- Natural or Counting numbers: 1, 2, 3, 4, 5, ... These allow for addition and
multiplication, some subtraction and some division.
- Whole numbers: 0, 1, 2, 3, 4, 5, ... These also allow for the operations of addition and
multiplication, and some subtraction and some division. The inclusion of 0 is actually
a big deal. Although we often teach kids to count with the
Counting or Natural numbers, it is the concept of zero that makes the system more complete and
facilitates computation. The concept of zero as a numeral comes to us from the Arabs.
- Integers: ..., -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, ...
These allow for addition, subtraction, and multiplication, along with some division.
- Rational numbers: There are two equivalent definitions of rational numbers. First, we could say that
rational numbers are the quotient of two integers (excluding division by 0). Thus, any number
that can be expressed in the form p/q where both p and q
are integers and q is not 0 is a rational number. This means that all fractions
are rational numbers and even values such as 7 which could be written as 7/1 or 28/4 are
rational numbers.
For the second definition of a rational number we could say that a rational number is
any number whose decimal representation either ends in all 0's or ends with an infinitely repeating
pattern of some number of digits. Using this definition, the values 7, 45.23, and 3.1416 are all rational
numbers because we understand each of them to have infinitely many 0's
after the final digit following the decimal point. At the same time, a number
such as 7.34343434... where it is understood
that the 34 pattern continues forever fits the definition of
a rational number.
- Irrational numbers: These are decimal numbers that are infinitely long but that do not have a repeating
sequence of digits. There are many irrational numbers but it is harder to write out examples since they
are infinitely long and yet do not repeat a set sequence of digits. We can construct some examples, such as
34.01002000300004... where we understand that pattern repeats (but the pattern is not a fixed group of
digits) so that we know that the next digits will be 000005 and that will be followed by 0000006 and so on.
There are other, more famous examples of irrational numbers, for example the square root of 2 but here all we
can do is to represent that number by a symbol,
 . .
- Real numbers: These are a combination of rational and irrational numbers, so they are all
of the decimal numbers.
- Imaginary numbers: These arise from taking the square root of a negative real number. The most important of
these is the square root of negative 1 which is called
 , so we really have the definition that , so we really have the definition that

- Complex numbers: These are numbers of the form
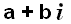 where a and b are real numbers. Interestingly, although we often write complex
numbers in the form
where a and b are real numbers. Interestingly, although we often write complex
numbers in the form 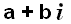 there is another convention that
expresses complex numbers in the form (a,b), again with
a and b being real numbers. there is another convention that
expresses complex numbers in the form (a,b), again with
a and b being real numbers.
|
| 2 | 22 |
The association of real numbers with distance is important. We use this first for the
number line and then for the coordinate plane and then for coordinates in three-space.
|
| 2 | 34 |
The use of text such as "Set of numbers x
with a 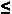 x x 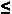 b
should have been given in the more formal b
should have been given in the more formal
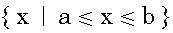
|
| 2 | 36 |
It is somewhat unfortunate, but mathematics, which is often praised for being so exact in its meanings, uses the
same notation for multiple things. Thus, (4,7) could indeed be the open interval on the number line
between 4 and 7. However, as noted above, it could also be the complex number that could have been
written as 4+7i. And, as we will see later, it could mean the point (4,7),
that is over 4 and up 7 from the origin
on the coordinate plane. The precise meaning has to be understood in the context of the
symbols. [Note that the symbols (7,4) could not mean an open interval since we always have the
left point of the interval on the left and the right point on the right. However, (7,4) could be either
the complex number 7+4i or the coordinate plane point that is over 7 and up 4 from the origin.]
|
| 5 | whole page |
It is important to go over each example. Also, point out that the square root function is not
addressed here. The book does get to it later, but we could also point out that the square root function is the same
as raising the value to the ½ power.
|
| 6 | 4 |
When the book gives the area as 2.0 sq. ft. they are sneaking in the significant digit argument.
They should have pointed out the difference between the math world and the real
world where measurement is always approximate.
|
| 6 | 38 |
There is little explanation of rounding, not to mention scientific notation. Both should be covered in the
lecture. Also, this would have been a good place to talk about how the calculator rounds.
Two web pages that give some help on this are TI-83 and rational numbers and
TI-83 and irrational numbers.
|
| 0.2 Exponents and Radicals |
| Page | Line # | Notes |
| 8-14 | all |
This is a ton of material to throw at students especially given that most of them will not need almost any of this in real life situations.
We will use some of this to derive a few formulae that we want for a specific purpose,
but once the work has been done once we can use the
result in the calculator without having to go back to all this math verbiage.
|
| 17 | 23 |
Presenting the distributive law is fine, but it should be accompanied
by the commutative and associate laws.
First, the distributive law is more precisely the
distributive property of multiplication over addition and/or subtraction.
The Commutative property of addition states that
a + b = b + a
for any real numbers a and b.
This means that we can commute, i.e., move, the
values being added so that the first becomes the second. This may seem trivial but we note that
there is no such property for subtraction. We know that
3 - 7  7 - 3
There is also a Commutative property of multiplication, using "*" to denote multiplication,
a * b = b * a
for any real numbers a and b. 7 - 3
There is also a Commutative property of multiplication, using "*" to denote multiplication,
a * b = b * a
for any real numbers a and b.
The Associative property of addition states that
a + (b + c) = (a + b) + c
for any real numbers a, b, and c.
Notice that the order of a, b, and c do not change. what changes is the association or grouping of the
values so that on the left side we need to add b and c first and then add a to that result while
on the right side we need to add a and b first and then add that sum to c. Again, there is no such rule for
subtraction and the example
12 - (9 - 1)  (12 - 9) - 1
demonstrates this. (12 - 9) - 1
demonstrates this.
There is an Associative property for multiplication stated as
a * (b * c) = (a * b) * c
for any real numbers a, b, and c.
|
| 0.3. Multiplying and Factoring Algebraic Expressions |
| Page | Line # | Notes |
| 18 | 18 |
The special forms are not a big deal for this course, but they are important if you are ever going to take a
standardized math test such as the SAT, ACT, or GRE. Recognizing these, along with 2 more,
can make a significant difference in your score on such tests. The other two are
a³ + b³ = (a + b)(a² - ab + b²) Sum of two cubes
a³ - b³ = (a - b)(a² + ab + b²) Difference of two cubes
|
| 20 | 3 |
There is nothing wrong with the "Trial and Error" method given in the book, but factoring a
trinomial of the form ax² + bx + c
does not have to be such a hit and miss operation. There is another
method, called "splitting the middle term" that gives you an orderly
set of steps to arrive at the correct answer.
See the SplitTheMiddle page for details.
|
| 0.4 Rational Expressions |
| Page | Line # | Notes |
| 22 | 38 |
Generally, cancellation is not a recognized rule. It is just the
popular term used when we really should be using the multiplicative property of 1.
The statement of the property is that
1*a = a*1 = a for any real number a.
The "rule" given should have been

|
| 25 | 40 |
The quadratic formula, again, is more useful on standardized tests than it is in real world situations.
Your will find some help in using the formula on the following pages: the
real number evaluation of a quadratic formula,
the real number symbolic evaluation of a quadratic formula, and
the complex number symbolic evaluation of a quadratic formula.
|
| 0.5 Solving Polynomial Expressions |
| Page | Line # | Notes |
| 27 | 30 |
Here, in the discussion of finding rational roots of a cubic equation of the form
ax³ + bx² + cx + d = 0
where a, b, c, and d are integers and a 0,
the book slips in the idea of factoring the cubic formula if we know or can find one of the roots, and
the books suggest we divide the cubic by the ()x-s) term to find the remaining
quadratic which may or may not be solvable over the real numbers. This is well beyond the rest of the material
in this book. It may be interesting to some, but you will not see it on any test or exam. 0,
the book slips in the idea of factoring the cubic formula if we know or can find one of the roots, and
the books suggest we divide the cubic by the ()x-s) term to find the remaining
quadratic which may or may not be solvable over the real numbers. This is well beyond the rest of the material
in this book. It may be interesting to some, but you will not see it on any test or exam.
However, one can use the calculator to find real roots, or at least great approximations
to real roots for any polynomial equation and this might be on a test or exam. The trick here is to
move to the more general
y = ax³ + bx² + cx + d
enter that into the calculator and then use the CALC:Zero option to find roots. A demonstration of this
may be done in class, especially if it is requested.
|
| 0.6 Solving Miscellaneous Equations |
| Page | Line # | Notes |
| 30-34 | all |
Hopefully, we can go over this in class and never see it again.
|
| 0.7 The Coordinate Plane |
| Page | Line # | Notes |
| 34-36 | all |
This is perhaps the most important section of this chapter.
We will use the coordinate plane
and later the coordinate space in a number of places in this course.
|
| 36 | 40 |
The distance formula is important! I believe that the authors of the book sneak in the delta notation here
without explaining it. It is not explained until page 76. We use 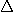 symbol,
the Capital delta character in the Greek alphabet,
to represent "change". So symbol,
the Capital delta character in the Greek alphabet,
to represent "change". So 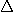 x means "the
change in x which is x2 - x1. x means "the
change in x which is x2 - x1.
|
| Page | Line # | Notes |
| 36 | 40 |
The Battleship program and problem will be presented in class to reinforce the
coordinate plane and the distance formula. There is a special web page devoted to
to go through a logical solution to the Battleship problem. You will find that page at
battleexplain.htm.
|
 .
.
 , so we really have the definition that
, so we really have the definition that

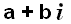 where a and b are real numbers. Interestingly, although we often write complex
numbers in the form
where a and b are real numbers. Interestingly, although we often write complex
numbers in the form 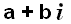 there is another convention that
expresses complex numbers in the form (a,b), again with
a and b being real numbers.
there is another convention that
expresses complex numbers in the form (a,b), again with
a and b being real numbers.
