Chapter 4, Section 1, Example 25

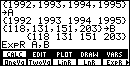
This problem is particularly interesting for a couple of reasons. The problem is to do an exponential regression on the data

Year	1992	1993	1994	1995
Heroin Deaths	118	131	151	203

We can do this on the TI-86 calculator by creating two lists, one for the year and one for the number of heroin deaths. Figure 1 shows two such lists, A and B, respectively. In addition, Figure 1 demonstrates the command that we need to create to do an exponential regression on the TI-86, namely, ExpR A,B

Figure 1

We formed the command in Figure 1, but the results of the command are shown in Figure 2.

Figure 2

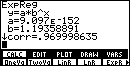
Note that the value of "a" in Figure 2 is 9.097*10^-152, the value of the base, "b", is given as 1.19358892, and that the correlation coefficient is given as 0.969998635. Of these values, the correlation coefficient is close to 1, indicating a "good" fit between the exponential model and the data that we have. Also, the base, "b" is essentially the same value given in the book, namely 1.2, in the solution. However, the book gives the constant value as 113 which is nowhere close to the value 9.097*10^-152 given in Figure 2. This difference between the book and the calculator is the first interesting aspect of the problem.

Before we had calculators that could do the computations to find the exponential regression equation we had to do the computations by hand. If you need to do computations by hand, you want to do them with small, reasonable, numbers. If we expect to find an equation of the form

y = a*b^x that will model our data, then we certainly do not want x to be values such as 1992, 1993, 1994, or 1995. It would be much easier for us to be using values of x such as 0, 1, 2, and 3. In fact, we would transpose the data to produce a new chart, such as

Year	1992	1993	1994	1995
Year number	0	1	2	3
Heroin Deaths	118	131	151	203

and then we would compute the regression equation for the "Year number" and the "Heroin Deaths". Then, if we want to use the regression equation to predict the deaths in 1996, we would recognize that 1996 corresponds to "Year number" 4 and we would use the value 4 for the exponent.

Figure 3 shows the creation of a new list, C, that has these "Year number" values, along with a new command to do an exponential regression, but this time using the lists C and B.

Figure 3

Figure 4 shows the result of the ExpR C,B command.

Figure 4

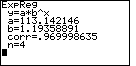
Note that the correlation coefficient has not changed, and that the base, b, has not changed. However, in Figure 4, we have a new value for the constant, a, namely, 113.142146, which is essentially the value given in the book for the soltuion.

We can go a step further and plot the points and the regression equation. Figure 5 displays the screen used to set up the scatter plot of the data points.

Figure 5

And, Figure 6 gives both that scatter plot and the plot of the regression equation.

Figure 6

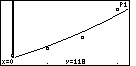
Now that we can see the plot of the points and the plot of the exponential regression equation, we might even want to question the original decision to use an exponential model for our data. The four data points might be just as linear as they are exponential. This is the second interesting aspect of the problem. For whatever reason, we made the choice to do an exponential regression. What are the consequences of that decision?

We can return to the main screen and give the command LinR C,B to do a linear regression. The result is shown in Figure 7.

Figure 7

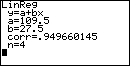
Note that the correlation coefficient for the linear regression is 0.949660145, which is just slightly lower than was the correlation coefficient for the exponential regression.

We can plot the new linear regression on the same plot that we had before. This produces Figure 8.

Figure 8

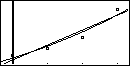
There is not much difference between the two graphs. We can magnify and enhance that difference, however, by changing the WINDOW settings. New settings are shown in Figure 9.

Figure 9

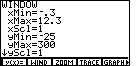
Figure 10 shows the scatter plot of the data values and a graph of the exponential regresssion equation. The new WINDOW settings give us a more clear impression of the exponential nature of the equation.

Figure 10

Figure 11 shows the data points and the linear regression equation.

Figure 11

And finally, Figure 12 contains both regression equations.

Figure 12

The difference in the equations is much more evident in Figure 12. If we use the equations to extrapolate new values, values for years beyond year number 3, then the exponential regression is going to predict much higher values for Heroin Deaths than will the linear regression.

We note that both forms of regression provide a "good" fit for the existing data. That is, both the linear and the exponential models do a good job of predicting the data that we do have. However, by choosing the exponential model we are ensuring that the prediction of Heroin Deaths for subsequent years will climb by larger and larger jumps.