
gnrnd4( key1=967170506, key2=6121050612, key3=8600004 ) L1 L2 lm_L2L1 <- lm(L2~L1) lm_L2L1 cor(L1,L2)These produce the console text in Figure 1.

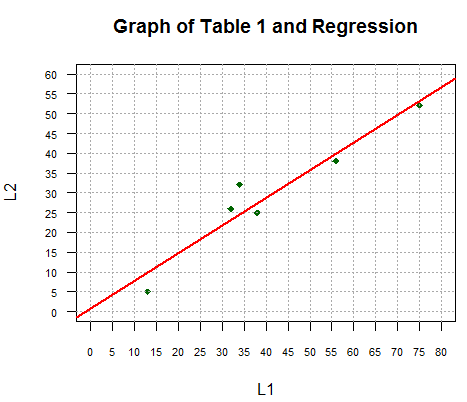
plot(L1,L2,xlim=c(0,80),xaxp=c(0,80,16),
ylim=c(0,60),yaxp=c(0,60,12),
main="Graph of Table 1 and Regression",
las=1, cex.axis=0.7, pch=18, col="darkgreen")
abline(v=seq(0,80,5), col="darkgray", lty=3)
abline(h=seq(0,60,5), col="darkgray", lty=3)
abline(lm_L2L1, col="red", lwd=2)
That plot is shown in Figure 2.
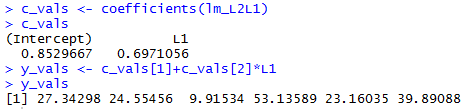
coefficients() function to pull those two values
out of the linear model.
The commands c_vals <- coefficients(lm_L2L1) c_vals y_vals <- c_vals[1]+c_vals[2]*L1 y_valsfirst retrieve the intercept and slope, i.e, the coefficient of x, from our model and store them in the variable c_vals. The intercept is stored in
c_vals[1]
and the slope is stored in c_vals[2].
Then we display the values in c_vals, noting that they are the
slightly longer versions of the values we saw in Figure 1. The statement
y_vals<-c_vals[1]+c_vals[2]*L1 uses those values, along with the
observed x values stored in L1, to implement the regression
equation and, therefore, to compute all of the expected y values.
Those are stored in the variable y_vals. The last line, y_vals,
then displays the values. We use this just so that we can see those values.
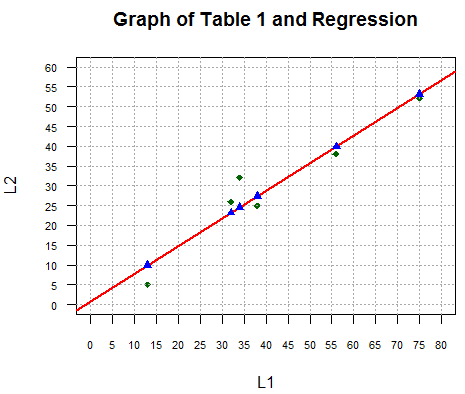
Those expected y values are the y coordinates for the associated x values of points on the regression line. We add the plot of these points to our graph via the command
points(L1,y_vals,pch=17,col="blue")with the result shown in Figure 4.
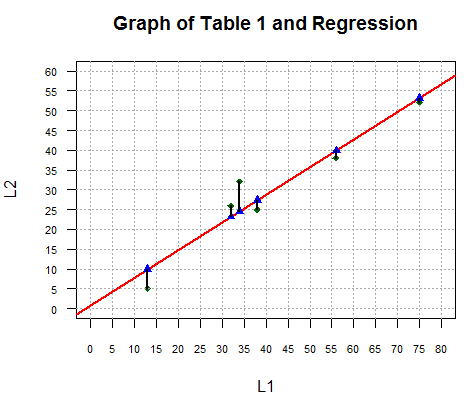
for(i in 1:length(L1))
{ lines(c(L1[i],L1[i]),c(L2[i],y_vals[i]),lwd=2)}
accomplishes this as we see in Figure 5.
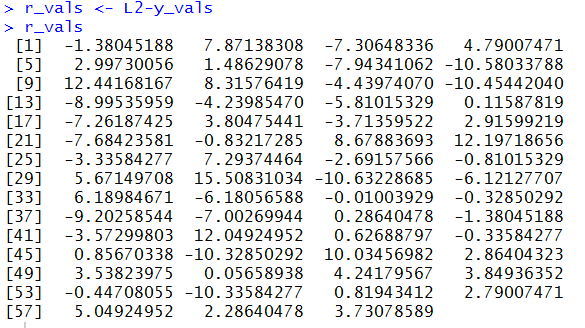
r_vals <- L2-y_vals r_valsfind those differences, store the differences in r_vals and then display those residual values. The console result is shown in Figure 6. [When matching the values shown in Figure 6 with the line segments shown in Figure 5 remember that the values in Figure 6 are associated, in order, with the values in L1. Looking back at Table 1 we see that those values in L1 were not given in ascending order. Therefore, we need to check the x value in Table 1 to determine which of the line segments in Figure 5 matches which of the values shown in Figure 6.]

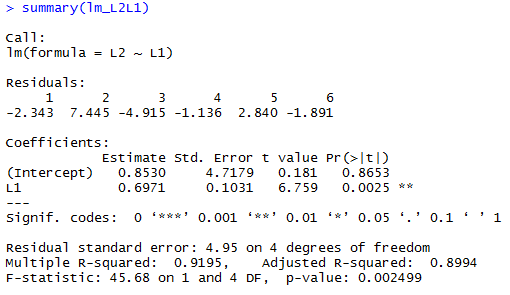
lm_resid<-residuals(lm_L2L1)
as shown in Figure 8.

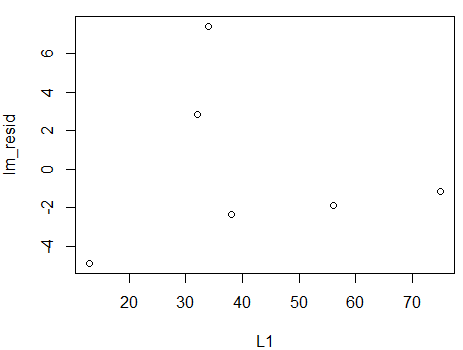
plot(L1,lm_resid)
will produce such a graph, in this case the gaph in Figure 9.
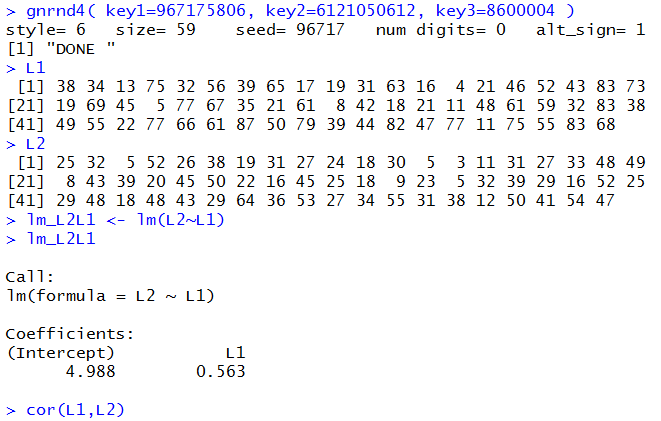
gnrnd4( key1=967175806, key2=6121050612, key3=8600004 ) L1 L2 lm_L2L1 <- lm(L2~L1) lm_L2L1 cor(L1,L2)to generate and display (just for verification) the data, as well as to create and display a new linear model. Console output is shown in Figure 10.
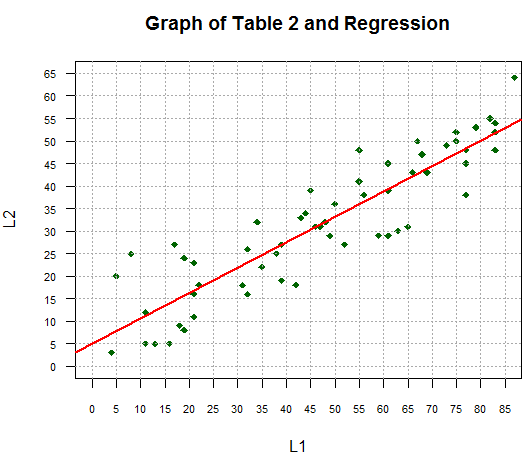
plot(L1,L2,xlim=c(0,85),xaxp=c(0,85,17),
ylim=c(0,65),yaxp=c(0,65,13),
main="Graph of Table 2 and Regression",
las=1, cex.axis=0.7, pch=18, col="darkgreen")
abline(v=seq(0,85,5), col="darkgray", lty=3)
abline(h=seq(0,65,5), col="darkgray", lty=3)
abline(lm_L2L1, col="red", lwd=2)
produce a graph, as shown in Figure 11.
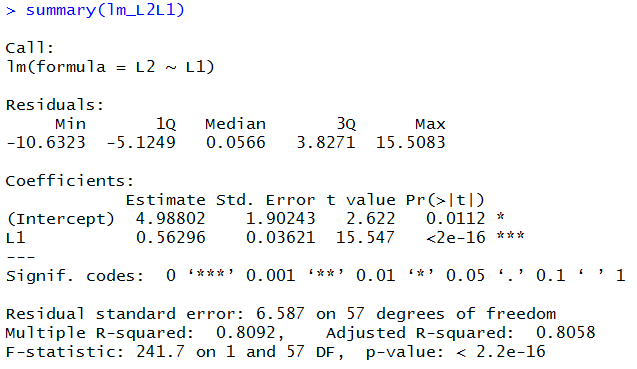
c_vals <- coefficients(lm_L2L1) c_vals y_vals <- c_vals[1]+c_vals[2]*L1 y_valswith the console output in Figure 12.

points(L1,y_vals,pch=17,col="blue")
for(i in 1:length(L1))
{ lines(c(L1[i],L1[i]),c(L2[i],y_vals[i]),lwd=2)}
changing the graph to that in Figure 13.
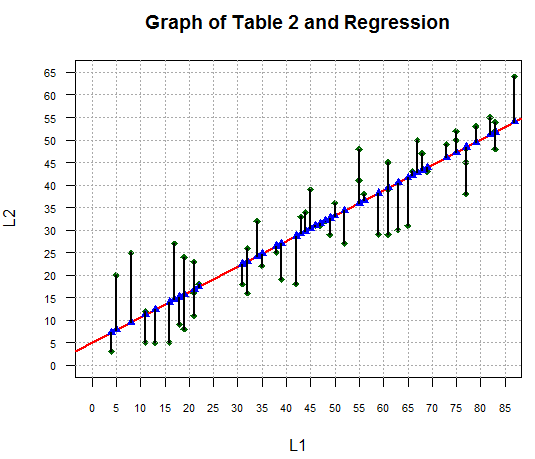
r_vals <- L2-y_vals r_valsas shown in Figure 14.
lm_resid <- residuals(lm_L2L1) lm_residto retrieve the residual values from our model and to display those values, as shown in Figure 16.

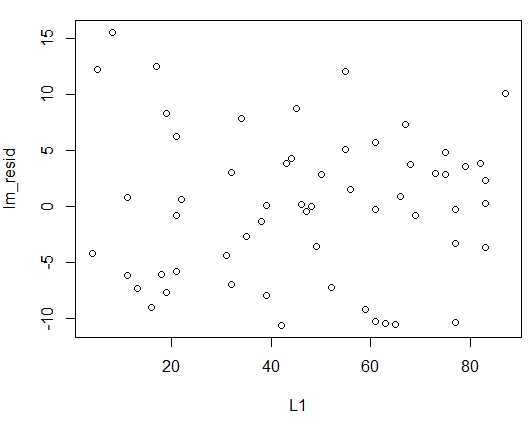
plot(L1,lm_resid) to plot
the residuals so that we can see that there is no real pattern to them.
The plot appears in Figure 17.
#This is a look at residuals in a linear regression
# first load gnrnd4 so that we can generate some numbers
source( "../gnrnd4.R")
# then here is a set of values to examine
gnrnd4( key1=967170506, key2=6121050612, key3=8600004 )
L1 # the x-values
L2 # the y-values
# how about a small plot of those values
plot( L1, L2 )
# now we will find the linear regression for those values
lm_L2L1 <- lm(L2~L1) # and save it in lm_L2_l1
# we can look at that model
lm_L2L1 # thus the linear equation is y=0.8530 + 0.6971*x
# we could get even more information about our
# linear model by using the summary function
summary( lm_L2L1 ) # you can find the same values in this
# and we can find the correlation coefficient
cor(L1,L2)
# take a moment here to generate a fancier plot
plot(L1,L2,xlim=c(0,80),xaxp=c(0,80,16),
ylim=c(0,60),yaxp=c(0,60,12),
main="Graph of Table 1 and Regression",
las=1, cex.axis=0.7, pch=18, col="darkgreen")
abline(v=seq(0,80,5), col="darkgray", lty=3)
abline(h=seq(0,60,5), col="darkgray", lty=3)
abline( h=0,v=0,col="black", lwd=2 ) # shade in the two axes
# then add the linear regression line
abline(lm_L2L1, col="red", lwd=2)
# L2 holds all of the observed y values
# Let us compute all of the expected y values
# rather than type in the coefficients, we will
# pull them out of our stored model
c_vals <- coefficients(lm_L2L1)
c_vals # and look at them again
# then we can use those coefficients to generate
# all of the expected y values
y_vals <- c_vals[1]+c_vals[2]*L1
# and here they are
y_vals
# we can add those to the plot. Of course they will
# all be on the regression line.
points(L1,y_vals,pch=17,col="blue")
# We can get a little fancy and draw in the
# difference between the observed and expected y values
for(i in 1:length(L1))
{ lines(c(L1[i],L1[i]),c(L2[i],y_vals[i]),lwd=2)}
# Or, we could find the length of those line segments
# by looking at the observed - expected y-values
r_vals <- L2-y_vals
r_vals # these are the residual values
# we actually saw those same residual values in the
# output of the summary command above.
# Let us do that command again to see the residual
# values that it displays.
summary( lm_L2L1 )
# The summary command, in this case, displayed the
# actual residual values. It did that because there were
# so few points and therefore there are only a small
# number of residual values. If there were more points,
# as we will see in the next example, then the summary
# function would not show the residuals.
# Our last concern with the residuals is that
# a plot of our x-values and the corresponding
# residual values does not show a pattern.
plot(L1,r_vals)
# However, we can still pull the residual values out of
# the model using the residuals function
lm_resid<-residuals(lm_L2L1)
lm_resid
##################################################
##################################################
# let us look at a problem with more data points
gnrnd4( key1=967175806, key2=6121050612, key3=8600004 )
L1 # the x-values
L2 # the y-values
# how about a small plot of those values
plot( L1, L2 )
# now we will find the linear regression for those values
lm_L2L1 <- lm(L2~L1) # and save it in lm_L2_l1
# we can look at that model
lm_L2L1 # thus the linear equation is y=4.988 + 0.563*x
# we could get even more information about our
# linear model by using the summary function
summary( lm_L2L1 ) # you can find the same values in this
# and we can find the correlation coefficient
cor(L1,L2)
# take a moment here to generate a fancier plot
plot(L1,L2,xlim=c(0,85),xaxp=c(0,85,17),
ylim=c(0,65),yaxp=c(0,65,13),
main="Graph of Table 2 and Regression",
las=1, cex.axis=0.7, pch=18, col="darkgreen")
abline(v=seq(0,85,5), col="darkgray", lty=3)
abline(h=seq(0,65,5), col="darkgray", lty=3)
abline( h=0,v=0,col="black", lwd=2 ) # shade in the two axes
# then add the linear regression line
abline(lm_L2L1, col="red", lwd=2)
# L2 holds all of the observed y values
# Let us compute all of the expected y values
# rather than type in the coefficients, we will
# pull them out of our stored model
c_vals <- coefficients(lm_L2L1)
c_vals # and look at them again
# then we can use those coefficients to generate
# all of the expected y values
y_vals <- c_vals[1]+c_vals[2]*L1
# and here they are
y_vals
# we can add those to the plot. Of course they will
# all be on the regression line.
points(L1,y_vals,pch=17,col="blue")
# We can get a little fancy and draw in the
# difference between the observed and expected y values
for(i in 1:length(L1))
{ lines(c(L1[i],L1[i]),c(L2[i],y_vals[i]),lwd=2)}
# Or, we could find the length of those line segments
# by looking at the observed - expected y-values
r_vals <- L2-y_vals
r_vals # these are the residual values
# The output of the summary command above did not
# give the actual residuals.
# Let us do that command again to see the residual
# values that it displays.
summary( lm_L2L1 )
# The summary command, in this case, displayed the
# Min, Q1 Median Q2 and Max values of the residuals.
# It did that because there were so many points
# and therefore there are so many residual values.
# However, we can still pull the residual values out of
# the model using the residuals function
lm_resid<-residuals(lm_L2L1)
lm_resid
# Our last concern with the residuals is that
# a plot of our x-values and the corresponding
# residual values does not show a pattern.
plot(L1,lm_resid)