Interpolation and Extrapolation

Return to Topics page
In the context of linear regressions, interpolation and extrapolation both involve finding the expected value(s), derived from the regression equation, based on independent variable values(s). [We will distinguish between interpolation and extrapolation below.] For example, if we have the equation y = 7.3633 + 0.5685*x, what is the expected value of y if the value of x is15?

To illustrate this, we will use the data in Table 1.
Here is one version of some commands that will generate that data and do a linear regression on it.

gnrnd4( key1=789321006, key2=6120480812, key3=5500010 )
L1
L2
summary(L1)
summary(L2)
lm_L2L1 <- lm(L2~L1)
lm_L2L1
cor(L1,L2)

Figure 1 holds the image of the console after running those commands.

Figure 1

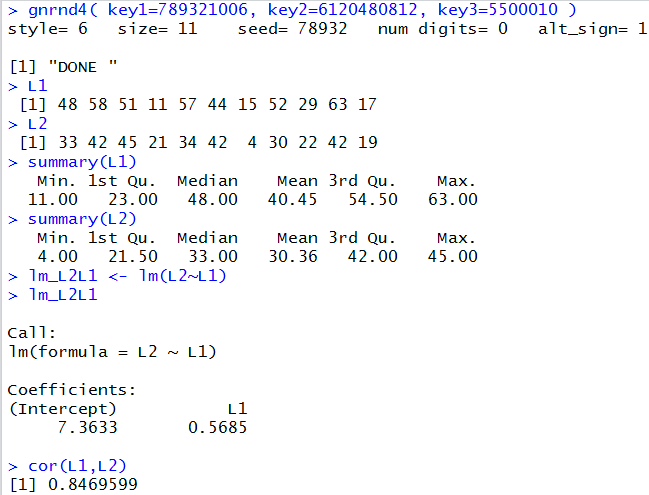
From the information in Figure 1 we see that the regression equation is y = 7.3633 + 0.5685*x.

The following commands generate the plot of the points and the regression line shown in Figure 2.

plot(L1,L2, xlab="x values", ylab="y values",
     main="Linear Regression Line for Table 1 Values",
     xlim=c(0,80), ylim=c(0,60),
     xaxp=c(0,80,16), yaxp=c(0,60,12),
     pch=19, col="green", las=1, cex.axis=0.7
     )
abline( v=seq(0,80,5),col="darkgray", lty=3)
abline( h=seq(0,60,5),col="darkgray", lty=3)
abline(lm_L2L1, col="green", lwd=2)

Figure 2

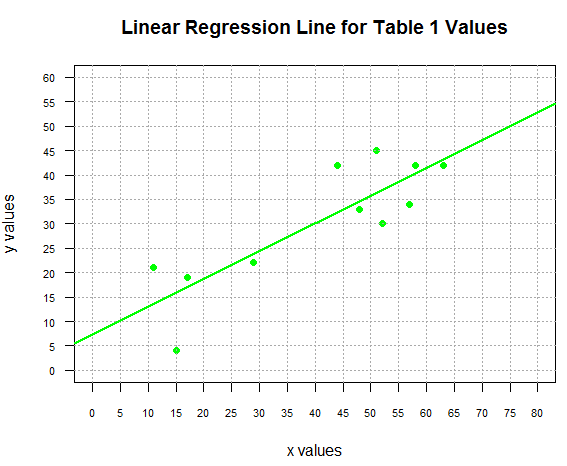
Let us return to our question. We have the equation y = 7.3633 + 0.5685*x, what is the expected value of y if the value of x is15?

Clearly, we just need to evaluate 7.3633 + 0.5685*15. We could do this by hand, on a calculator, or on the computer. Using R, we could just give the command 7.3633+0.5685*15 and get the results, as shown in Figure 3.

Figure 3

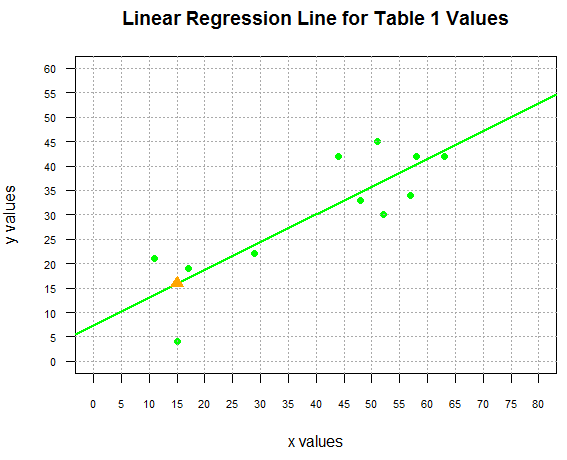
What we have found is that the point (15,15.8908) is on our regression line. We can add that point to our plot by giving the command points(15,15.8908, pch=5, col="orange", cex=1.5) and we can see this in Figure 4.

Figure 4

In Figure 3 we saw how to find one point on the line, but what if we want to find a number of points, say all of the points with x values from 20 to 55 in steps of 5? One solution, just to find the dependent y values, would be to use the command 7.3633+0.5685*seq(20,55,5) shown in the console image in Figure 5

Figure 5

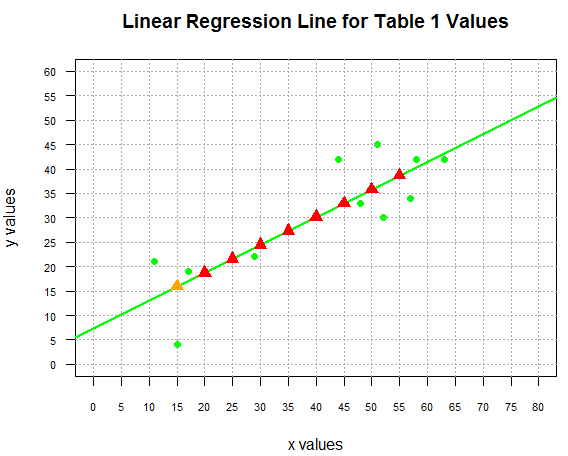
Now that we know those values we could create a points() command for each of them. But that seems a bit much.

A more efficient approach is to put all of the independent x values into a variable, use that variable to create a corresponding sequence of dependent y values and then plot the two sequences in one points() command. We could do this with

x_vals <- seq(20,55,5)
y_vals <- 7.3633+0.5685*x_vals
points(x_vals,y_vals, pch=17, col="red", cex=1.5)

with the result being shown in Figure 6.

Figure 6

Of course, part of the process that we just went through involved reading the output of the lm() command, shown back in Figure 1, to find the values for the intercept and coefficient of x. Then we had to transcribe those values to form our commands, such as y_vals<-7.3633+0.5685*x_vals. It might have been better if we could have R find and use those values directly. The following commands do just that

c_vals <- coefficients(lm_L2L1)
c_vals
x_vals <- seq(22.5,57.5,5)
y_vals <- c_vals[1]+c_vals[2]*x_vals
points(x_vals,y_vals, pch=17, col="blue")

In an earlier page we had seen the use of the coefficients() command to extract the desired values from the model. In the commands above, we follow that with a command that just displays the extracted values. We use that command, in this example, just to confirm the values. This is shown in Figure 7.

Figure 7

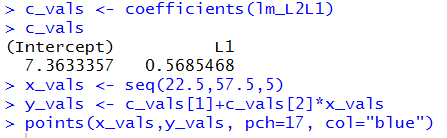
The values shown in Figure 7 have more significant digits than what we saw in Figure 1. By using the coefficients() function to extract those values we will be able to use the slightly more exact representation of the true value (remember that even our new values are just rounded to 7 secimal places).

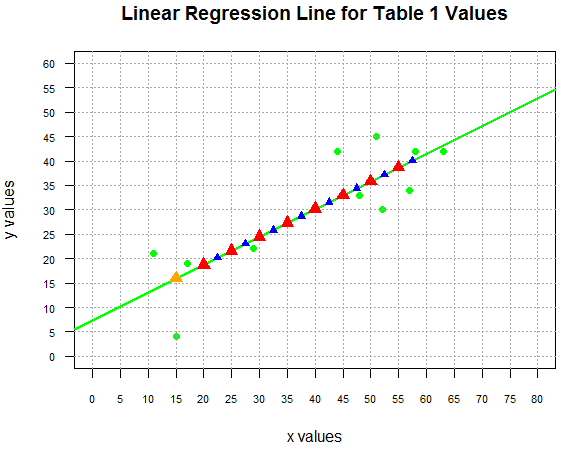
Returning our attention to the commands listed above, to demonstrate using the extracted values we create a new sequence of independent x values and use them to compute, via the two values in c_vals, the corresponding dependent y values. These new values are then used to plot the new points, shown in Figure 8.

Figure 8

Of course, if we had actually wanted to know those dependent values, rather than trying to read them from the graph we could just use the command y_vals to get the values displayed in the console pane, shown in Figure 9.

Figure 9

Interpolation

All of the values that we have computed above are examples of interpolation because all of those values fell within the range of the x values. Notice, back in Figure 1, when we displayed the summary(L1) that the minimum value was 11 and the maximum value was 63. In each instance above, the x values that we used fell between the minimum and maximum values in L1. We feel somewhat safe in interpolating values within this range because we have observed values that surround the values we are interpolating.

This particular example does provide us with a region where we have a gap in the x values in the original data, namely, we jump from 29 to 44. That means that we do not have any observed values in that region. Nonetheless, we have values around the gap and therefore, we still feel comfortable doing the interpolation.

Extrapolation

We have not seen any examples of extrapolation to this point. We extrapolate when we use the regression equation to produce a y value from an x value that is outside the range of the observed x values. Thus, in our example, if we were to ask for the expected value when x=80 we would be doing an extrapolation. The mathematics is the same. We could just use the command 7.3633+0.5685*80 to compute the value, finding that it is 52.8433 and we could plot that point via points(80,52.8433, pch=25, col="brown", cex=1.5) as shown in Figure 10.

Figure 10

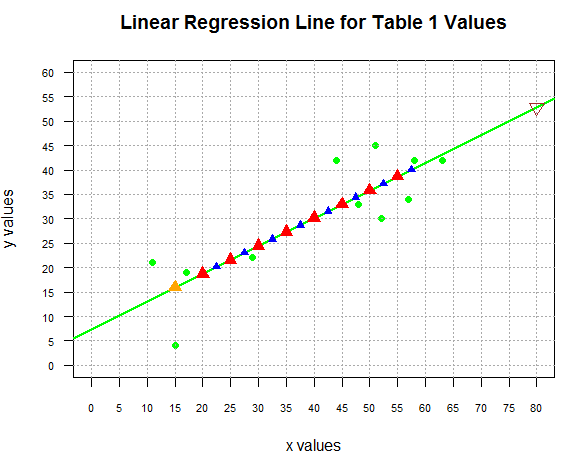
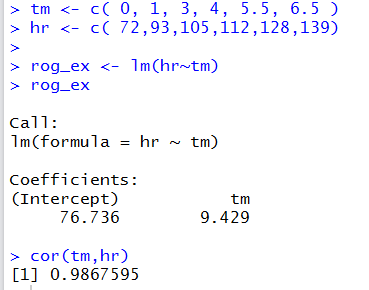
Although we "can" do the extrapolation we should be quite cautious about doing so. The model that we have, the straight line model, is derived from the observed points. We feel somewhat confident that the model is a good one though not a great one since the correlation coefficient shown back in Figure 1 was 0.8469599. However, we have no particular indication that the model will hold beyond (on either the low or the hgh side) the observed data range.

Let us explore this with some real life data. As it turns out, I have been keeping track of my heart rate during exercise. I have the following table of values.
We can use the following commands

tm <- c( 0, 1, 3, 4, 5.5, 6.5 )
hr <- c( 72,93,105,112,128,139)

rog_ex <- lm(hr~tm)
rog_ex
cor(tm,hr)

to create our model of this data. The result is shown in Figure 11.

Figure 11

We can use the following commands

plot( tm,hr, xlab="Time in minutes",
      ylab="Heart Rate in beats per minute",
      main="Roger's Exercise Record",
      xlim=c(0,10), xaxp=c(0,10,10),
      ylim=c(0,220), yaxp=c(0,220,22),
      pch=19, col="red", las=1, cex.axis=0.7
      )
abline( v=seq(0,10,1), col="darkgray", lty=3)
abline( h=seq(0,220,10), col="darkgray", lty=3)
abline( rog_ex, col="blue", lwd=2)

to generate the plot in Figure 12.

Figure 12

From Figure 11 and Figure 12 it seems that our linear model is quite good. We can get interpolated values for minutes 1 through 6 by performing the following commands:

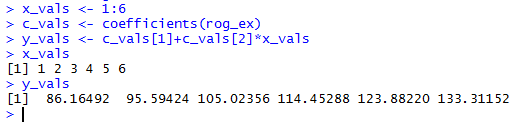
x_vals <- 1:6
c_vals <- coefficients(rog_ex)
y_vals <- c_vals[1]+c_vals[2]*x_vals
x_vals
y_vals

and the results of those commands are shown in Figure 13.

Figure 13

Then we can add those points to the graph via the command points(x_vals, y_vals, pch=6, col="darkgreen") to produce the image shown in Figure 14.

Figure 14

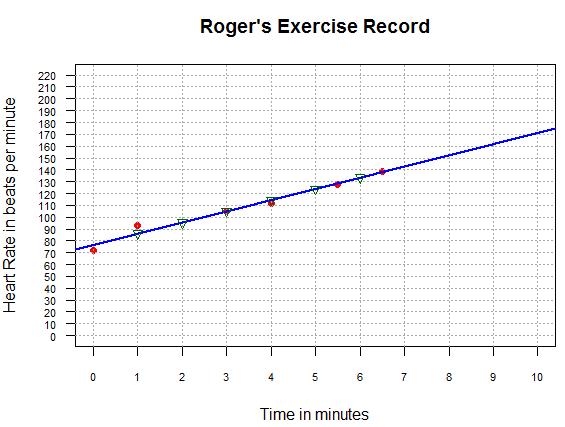
The values that we found for time equal to 2, 5, and 6 minutes, namely, about 96, 124, and 133, are quite likely to be really close to the actual values that I experienced in that exercise session.

On the other hand, we could follow the similar steps to extrapolate valeus for time equal to 10, 20, and 30 minutes. The commands that we use would be

x_vals <- seq(10,30,10)
c_vals <- coefficients(rog_ex)
y_vals <- c_vals[1]+c_vals[2]*x_vals
x_vals
y_vals

and the results of those commands are shown in Figure 15.

Figure 15

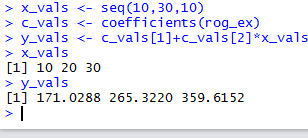
These results demonstrate the danger of extrapolation. We can certainly compute the values but a quick examination of the results shows that they cannot be accurately predicing my heart rate at those times. For those of you who are not familiar with human heart rates I will merely point out that at my age my expected maximum heart rate is about 150. Or, to put it more bluntly, if I were to exercise hard enough to try to get my heart rate to 170 I would certainly pass out before reaching that goal. Getting my heart rate to 265 or 360 is just not going to happen.

What we see here is that the recorded data, the original data in Table Roger's Exercise Record, represents a pattern of increasing heart rate over time. That pattern just cannot be sustained over a longer period of time. The model for the first 6 minutes cannot be the model for the following 24 minutes.

The absurdity of blindly applying the model to values outside the observed range is even more evident if we were to extrapolate to predict my hear rate ten minutes before I started to exercise. That computation, which we could do, would produce a negative heart rate at time -10 minutes.

Return to Topics page
©Roger M. Palay Saline, MI 48176 November, 2015