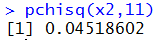Hypothesis Test for Population Standard
Deviation for normal population
Return to Topics page
The situation is:
- We have a population
that is normally distributed.
For this situation it is important that the population
has a normal distribution but we do not
need to know, ahead of time,
the mean or standard deviation of that distribution.
- We are interested in the standard deviation,
σ, of the population.
- We have a hypothesis about the "true" value of
the population standard deviation.
That is, someone (perhaps us) claims that
H0: σ = a,
for some value a.
- We will consider an alternative
hypothesis which is one of the following
- H1: σ > a,
- H1: σ < a, or
- H1: σ ≠ a.
- We want to test
H0 against
H1.
- We have already determined
the level of significance that we will use for this test.
The level of significance, α,
is the chance that we are willing to take that
we will make a Type I error,
that is, that we will reject H0
when, in fact, it is true.
|
Immediately, we recognize that samples
of size n drawn from this population
will have a distribution of the ratio
of n-1 times the
sample variance to the population variance that is a
χ² with n-1 degrees of freedom.
Thus, if H0 is true and the population
standard deviation is a, then for samples of size n
the statistic  will have a χ² distribution with n-1 degrees
of freedom.
will have a χ² distribution with n-1 degrees
of freedom.
At this point we proceed via
the critical value approach
or by the attained significance approach.
These are just different ways to
create a situation where we can finally make a decision.
The critical value approach tended to be used
more often when everyone needed to use the tables.
The attained significance approach is more commonly
used now that we have calculators and computers
to do the computations. Of course either approach can be done
with tables, calculators, or computers.
Either approach gives the same final result.
|
- We determine a sample size n.
This will set the number of degrees of freedom
as we use the χ² distribution.
|
Critical Value Approach
- Find the value or values (depending upon if we are
looking at a one-tailed or a two-tailed test)
of χ² that have the level of significance area
outside of the value or values. For a two-tailed
test (H1: σ ≠ a)
we need to split the level of significance so that half is at
the low end and half is at the right end. [This is
made somewhat more complex if you are using a table since most tables
only give the upper tail value and because χ² is
not a symmetric distribution.]
Use that value or those values as the critical values.
- Take the random sample of size n and compute the
sample standard deviation, s, from that sample.
- Compute the value
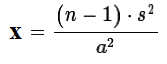 . .
- If that value is beyond the critical value(s)
then we say that
"we reject H0 in favor of
the alternate H1". If that
value
is not more extreme than the critical value(s)
then we say "we have insufficient
evidence to reject H0".
| |
Attained significance Approach
- We compute the sample standard deviation, s.
- Compute
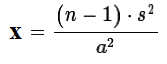 . .
- Using the χ² distribution,
and taking into account the alternative hypothesis,
H1, so that we know
if we are doing a one-tail or two-tail
test,
we compute the probability of getting the value
χ2 or a value more extreme than that.
- If the resulting probability is smaller than or equal to the
predetermined level of significance then we say that
"we reject H0 in favor of
the alternate H1". If the
resulting
probability is not less than the predetermined level of significance
then we say "we have insufficient evidence to reject H0".
|
We will work our way through an example to see this.
Assume that we have a normal population of values.
I claim that the true standard deviation, σ
of those values is 8.5. You suspect that the true
standard deviation is not 8.5 but rather some value less than that.
We agree to test the null hypothesis
H0: σ = 8.5
against the alternative hypothesis
H1: σ < 8.5
at the 0.05 level of significance.
To do this we agree to take a random sample of size 12 from
the population and then compute the sample standard deviation, s.
If s is far enough below 8.5 we will reject
H0 in favor of
H1.
The question is, how far below 8.5 is far enough so that
if the null hypothesis is true then we will reject it
no more than 5% of the time based upon a sample of size 12?
The critical value approach has us look
to the χ² distribution
for n-1, that is 11 degrees of freedom and to find the
χ² value that has 5% of the area under the curve to the left of
that value.
We could use a table, a calculator, or the computer to get this.
The result is the value 4.575, rounded to 3 decimal places.
Remember, 4.575 is the χ² value.
We need to compute the test statistic from
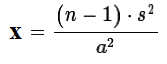 and
compare that value against 4.575.
and
compare that value against 4.575.
We take a sample, shown in Table 1.
If we assign that value to s then we can compute
our test statistic as 11*s*s/(8.5^2), which turns out to be about
4.451, a value that is less than our
critical value of 4.575. Therefore, based on that sample,
we reject H0 in favor of
H1 at the 0.05 level of significance.
The computations that we did above are shown in Figure 1.
Figure 1
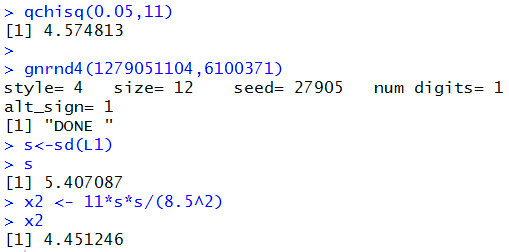
To do the same problem using the attained significance
approach, we take our sample of size 12 shown in Table 1, we find the
sample standard deviation which we found to be s=5.407087,
we compute our test statistic, x2=4.451246 and then we
find the area under the curve to the left of that value for 11 degrees
of freedom. The R command to do this is
pchisq(x2,11). If that value is less than
our predetermined level of significance, in this
case 5%, then we reject H0.
The console view of the command is shown in Figure 2.
Figure 2
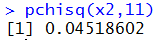
Indeed, the result is 0.045 which is less than the 5% significance level
for the problems. Therefore, we reject H0
just as we did using the critical value approach.
In all fairness, I wanted to demonstrate such a rejection.
As such, I created a call to gnrnd4() that I knew woud
produce the result that I wanted to use as an example.
Table 2 gives more a more fair sample. It really is drawn
from a population that has a standard deviation of 8.5.
Of course, each time this page is reloaded we get a new sample
in Table 2. Therefore, you could repeatedly refresh this
page and see how the values of the
sample standard deviation, s, and the test statistic, x2,
change with each new sample. Furthermore, using the critical value
approach, we know that we will reject H0
about 5% of the time.
A second example:
We assume that we have a normal population of values and
that the
null hypothesis is that the standard deviation of the population is
24.38. The alternative hypothesis is that
the true population standard deviation is greater than 24.38.
We want to test the null hypothesis,
H0: σ = 24.38,
against the alternative hypothesis,
H1: σ > 24.38,
at the 0.025 level of significance.
We decide to take samples of size 22.
For the critical value approach we use the fact
that if we take samples of size 22, compute the sample standard deviation, s,
for each sample, then compute 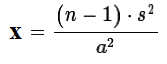 for each such sample, the value x will have a χ²
distribution with 21 degrees of freedom.
From the χ² tables or from a calculator or from the computer
we determine that at 21 degrees of freedom the
χ² value 35.479 has
2.5% of the area under the curve to its right.
Therefore, we set our critical value at 35.479.
for each such sample, the value x will have a χ²
distribution with 21 degrees of freedom.
From the χ² tables or from a calculator or from the computer
we determine that at 21 degrees of freedom the
χ² value 35.479 has
2.5% of the area under the curve to its right.
Therefore, we set our critical value at 35.479.
Next we take a random sample. Our sample is shown in Table 3.
A third example:
We assume that we have a normal population of values and
that the
null hypothesis is that the standard deviation of the population is
3.25. The alternative hypothesis is that
the true population standard deviation is not equal to 3.25 .
We want to test the null hypothesis,
H0: σ = 3.25,
against the alternative hypothesis,
H1: σ ≠ 3.25,
at the 0.0333 level of significance.
Note that this is a two-tailed test.
We will reject H0 if our sample standard deviation is either
too high or too low. We will need χ² values that
give us 1.6666% of the area below the low value and 1.6666% of the area above to high value.
We decide to take samples of size 15.
For the critical value approach we use the fact
that if we take samples of size 15, compute the sample standard deviation, s,
for each sample, then compute 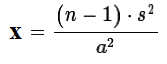 for each such sample, the value x will have a χ²
distribution with 14 degrees of freedom.
From the χ² tables or from a calculator or from the computer
we determine that at 14 degrees of freedom the
χ² value 5.1676 has
1.6666% of the area under the curve to its left,
while the χ² value 27.4809 has
1.6666% of the area under the curve to its right,
Therefore, we set our critical values at 5.1676 and 27.4809.
for each such sample, the value x will have a χ²
distribution with 14 degrees of freedom.
From the χ² tables or from a calculator or from the computer
we determine that at 14 degrees of freedom the
χ² value 5.1676 has
1.6666% of the area under the curve to its left,
while the χ² value 27.4809 has
1.6666% of the area under the curve to its right,
Therefore, we set our critical values at 5.1676 and 27.4809.
Next we take a random sample. Our sample is shown in Table 4.
Using the attained significance approach in
this last example was a bit more tricky.
If you reload this page a number of times you will see that the
R command that we used changed, as needed, between
pchisq(x2,14) and pchisq(x2,14,lower.tail=FALSE).
Our sample gives a sample standard deviation that is either lower
than or higher than the H0 value, 3.25.
If it is lower then we need to ask is it low enough to reject H0.
If it is higher then we need to ask is it high enough to reject H0.
Thus, depending on the sample standard deviation we need to choose
which tail we want to use, and that determines the form of the pchisq()
command to use.
We will take that into account below when we formulate a function to do all of
this in one step.
The following function definition for hypoth_test-sigma()
incorporates all of the steps for the various cases that we have
seen above. The file that holds this function is available for
download at hypo_sigma.R.
# Roger Palay copyright 2016-02-08
# Saline, MI 48176
#
hypoth_test_sigma <- function(
H0_sigma, n, samp_sigma, H1_type, sig_level=0.05)
{ # perform a hypothsis test for the population
# standard deviation=H0_sigma
# based on a sample of n items yielding a
# sample standard deviation, samp_sigma,
# where the alternative hypothesis is
# != if H1_type==0
# < if H1_type < 0
# > if H1_type > 0
# Do the test at sig_level significance,
#
# It is important that the population is a normal
# distribution.
decision <- "Reject"
x2 <- (n-1)*(samp_sigma^2)/(H0_sigma^2)
if( H1_type < 0 )
{ crit_low <- qchisq( sig_level, n-1 )
crit_high <- "n.a."
if( x2 > crit_low )
{ decision <- "Do Not Reject" }
attained <- pchisq( x2, n-1 )
alt <- paste("sigma < ", H0_sigma)
}
else if( H1_type > 0 )
{ crit_high <- qchisq( sig_level, n-1, lower.tail=FALSE )
crit_low <- "n.a."
if( x2 < crit_high )
{ decision <- "Do Not Reject" }
attained <- pchisq( x2, n-1, lower.tail=FALSE )
alt <- paste("sigma > ", H0_sigma)
}
else
{ crit_low <- qchisq( sig_level/2, n-1 )
crit_high <- qchisq( sig_level/2, n-1, lower.tail=FALSE )
if (x2 >crit_low & x2 < crit_high )
{ decision <- "Do Not Reject" }
if( samp_sigma < H0_sigma )
{ attained =2*pchisq( x2, n-1 ) }
else
{ attained =2*pchisq( x2, n-1, lower.tail=FALSE ) }
alt <- paste("sigma != ", H0_sigma)
}
result <- c(H0_sigma, n, samp_sigma, alt, sig_level,
crit_low, crit_high, x2, attained,
decision)
names(result) <- c("H0_sigma","Sample Size",
"Samp Sigma", "H1", "sig level",
"crit low","crit high","chi2 val",
"attained","Decision")
return( result )
}
Table 5 gives six illustrations of problems involving
hypothesis testing for the popultion standard deviation.
| Table 5: Case studies |
| Case |
H0 |
Sample
Size |
Sample
Standard
Deviation |
H1 |
Level of
Significance |
| I |
H0: σ = 4.63 |
16 |
3.24 |
H1: σ < 4.63 |
0.075 |
| II |
H0: σ = 4.63 |
16 |
3.57 |
H1: σ < 4.63 |
0.075 |
| III |
H0: σ = 18.43 |
32 |
22.52 |
H1: σ > 18.43 |
0.02 |
| IV |
H0: σ = 18.43 |
32 |
23.45 |
H1: σ > 18.43 |
0.02 |
| V |
H0: σ = 7.35 |
28 |
5.78 |
H1: σ ≠ 7.35 |
0.08 |
| VI |
H0: σ = 7.35 |
41 |
5.78 |
H1: σ ≠ 7.35 |
0.08 |
To perform the hypothesis test for Case I we use the command
hypoth_test_sigma( 4.63, 16, 3.24, -1, 0.075)
Figure 3 holds the console image of this command.
Figure 3

This is a one tail test using the lower tail.
Using the critical value approach we find that
the critical value is 7.9695. The computed
statistic is 7.345, which is even lower than the
critical value. Therefore we reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.0526
which is less than the given
significance level of 0.075.
Therefore we reject
H0.
To perform the hypothesis test for Case II we use the command
hypoth_test_sigma( 4.63, 16, 3.57, -1, 0.075)
Figure 4 holds the console image of this command.
Figure 4
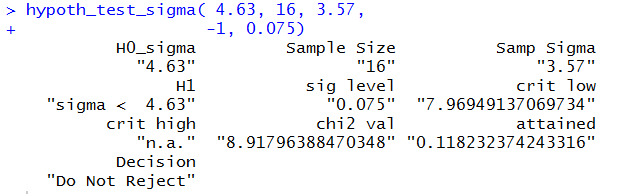
This is a one tail test using the lower tail.
Using the critical value approach we find that
the critical value is 7.9695. The computed
statistic is 8.918, which is higher than the
critical value. Therefore we do not reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.1182
which is greater than the given
significance level of 0.075.
Therefore we do not reject
H0.
To perform the hypothesis test for Case III we use the command
hypoth_test_sigma( 18.43, 32, 22.52, 1, 0.02)
Figure 5 holds the console image of this command.
Figure 5
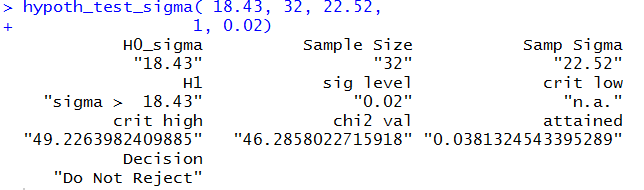
This is a one tail test using the upper tail.
Using the critical value approach we find that
the critical value is 49.226. The computed
statistic is 46.258, which is lower than the
critical value. Therefore we do not reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.03813
which is greater than the given
significance level of 0.02.
Therefore we do not reject
H0.
To perform the hypothesis test for Case IV we use the command
hypoth_test_sigma( 18.43, 32, 23.45, 1, 0.02)
Figure 6 holds the console image of this command.
Figure 6

This is a one tail test using the upper tail.
Using the critical value approach we find that
the critical value is 49.226. The computed
statistic is 50.1876, which is higher than the
critical value. Therefore we reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.016
which is less than the given
significance level of 0.02.
Therefore we reject
H0.
To perform the hypothesis test for Case V we use the command
hypoth_test_sigma( 7.35, 28, 5.78, 0, 0.06)
Figure 7 holds the console image of this command.
Figure 7
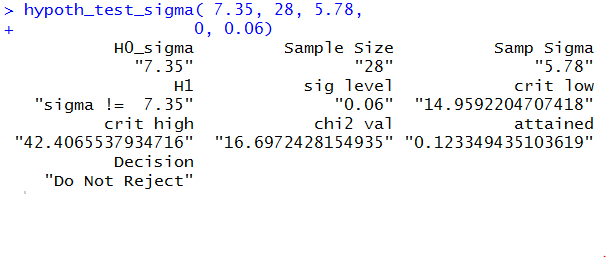
This is a two tail test using
both a lower and upper tail,
each having half of the area specified by the
level of significance.
Using the critical value approach we find that
the critical values are 14.959
and 42.4066. The computed
statistic is 16.697, which is between the
critical values. Therefore we do not reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.123
which is greater than the given
significance level of 0.06.
Therefore we do not reject
H0.
To perform the hypothesis test for Case VI
we use the command
hypoth_test_sigma( 7.35, 41, 5.78, 0, 0.06)
Figure 8 holds the console image of this command.
Figure 8
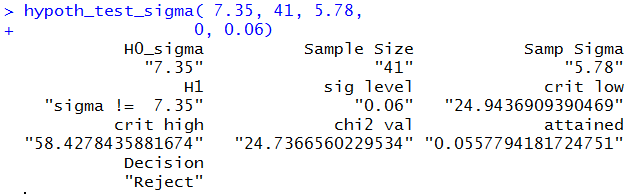
This is a two tail test using
both a lower and upper tail,
each having half of the area specified by the
level of significance.
Using the critical value approach we find that
the critical values are 24.94379
and 58.4278. The computed
statistic is 24.7367, which is not between the
critical values. Therefore we reject
H0.
Using the attained significance approach,
we find the
attained significance is 0.0558
which is less than the given
significance level of 0.06.
Therefore we reject
H0.
Below is a listing of the R commands
used in generating this page.
source("../gnrnd4.R")
qchisq(0.05,11)
gnrnd4( key1=1279051104, key2=0006100371 )
gnrnd4( key1=1500541104, key2=0008500578 )
s<-sd(L1)
s
x2 <- 11*s*s/(8.5^2)
x2
pchisq(x2,11)
qchisq(0.025,21,lower.tail=FALSE)
# sample that rejects the null hypothesis
gnrnd4( key1=2787062104, key2=0243819982 )
L1
s<-sd(L1)
s
x2 <- 21*s*s/(24.38^2)
x2
pchisq(x2,21,lower.tail=FALSE)
# another sample that rejects the null hypothesis
gnrnd4( key1=2332182104, key2=0243840658 )
L1
s<-sd(L1)
s
x2 <- 21*s*s/(24.38^2)
x2
pchisq(x2,21,lower.tail=FALSE)
# sample that does not reject the null hypothesis
gnrnd4( key1=2864272104, key2=0243844528 )
L1
s<-sd(L1)
s
x2 <- 21*s*s/(24.38^2)
x2
pchisq(x2,21,lower.tail=FALSE)
qchisq(0.01666, 14)
qchisq(0.01666, 14, lower.tail=FALSE)
# sample that rejects the null hypothesis
# for two-tailed test at 0.03333 level
gnrnd4( key1=2791411404, key2=0032524217 )
L1
s<-sd(L1)
s
x2 <- 14*s*s/(3.25^2)
x2
pchisq(x2,14)
pchisq(x2,14,lower.tail=FALSE)
# sample that does not reject the null hypothesis
# for two-tailed test at 0.03333 level
gnrnd4( key1=2364551404, key2=0032515898 )
L1
s<-sd(L1)
s
x2 <- 14*s*s/(3.25^2)
x2
pchisq(x2,14)
pchisq(x2,14,lower.tail=FALSE)
source("../hypo_sigma.R")
hypoth_test_sigma( 4.63, 16, 3.24,
-1, 0.075)
hypoth_test_sigma( 4.63, 16, 3.57,
-1, 0.075)
hypoth_test_sigma( 18.43, 32, 22.52,
1, 0.02)
hypoth_test_sigma( 18.43, 32, 23.45,
1, 0.02)
hypoth_test_sigma( 7.35, 28, 5.78,
0, 0.06)
hypoth_test_sigma( 7.35, 41, 5.78,
0, 0.06)
Return to Topics page
©Roger M. Palay
Saline, MI 48176 February, 2016
 will have a χ² distribution with n-1 degrees
of freedom.
will have a χ² distribution with n-1 degrees
of freedom.
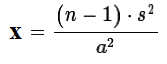 .
.
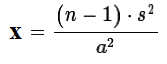 .
.