Hypothesis test for Population Mean,
based on the sample mean, σ known
Return to Topics page
The situation is:
- We have a hypothesis about the "true" value of a population mean.
That is, someone (perhaps us) claims that H0: μ = a,
for some value a.
- By some miracle, we happen to know the
population standard deviation, σ.
- We will consider an alternative hypothesis which is one of the following
- H1: μ > a,
- H1: μ < a, or
- H1: μ ≠ a.
- We want to test
H0 against H1.
- We have already determined
the level of significance that we will use for this test.
The level of significance, α,
is the chance that we are willing to take that
we will make a Type I error,
that is, that we will reject H0
when, in fact, it is true.
|
|
Immediately, we recognize that samples
of size n drawn from this population
with have a distribution of the
sample mean that is a
normal with mean=μ and
standard deviation=σ/sqrt(n).
At this point we proceed via
the critical value approach
or by the attained significance approach.
These are just different ways to
create a situation where we can finally make a decision.
The critical value approach tended to be used
more often when everyone needed to use the tables.
The attained significance approach is more commonly
used now that we have calculators and computers
to do the computations. Of course either approach can be done
with tables, calculators, or computers.
Either approach gives the same final result.
|
|
Critical Value Approach
- We find the z-score that corresponds to
having the level of significance area more extreme than that z-score,
remembering that if we are looking at being either too low or too high
then we need half the area in both extremes.
- We determine a sample size n.
- Compute
the sx = σ / sqrt(n)
and use that value to
compute (z)(sx).
- Set the critical value (or values in the case of a two-sided test)
such that it (they) mark the value(s) that is (are) that distance,
(z)(sx),
away from the mean given
by H0: μ = a.
- Then, we take a random sample of size n from the population.
- We compute the sample mean,
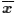 . .
- If that mean
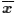 is more extreme than the critical value(s)
then we say that
"we reject H0 in favor of
the alternate H1". If the
sample mean
is not more extreme than the critical value(s)
then we say "we have insufficient evidence to reject H0". is more extreme than the critical value(s)
then we say that
"we reject H0 in favor of
the alternate H1". If the
sample mean
is not more extreme than the critical value(s)
then we say "we have insufficient evidence to reject H0".
| |
Attained significance Approach
- Then, we take a random sample of size n from the population.
- We compute the sample mean,
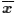 . .
- Assuming that H0 is true,
we compute the probability of getting the value
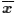 or a value more extreme than that.
We can do this using the fact that the distribution of
sample means for samples of size n is normal
with mean=μ and standard deviation=σ/sqrt(n). or a value more extreme than that.
We can do this using the fact that the distribution of
sample means for samples of size n is normal
with mean=μ and standard deviation=σ/sqrt(n).
- If the resulting probability is smaller than or equal to the
predetermined level of significance then we say that
"we reject H0 in favor of
the alternate H1". If the
resulting
probability is not less than the predetermined level of significance
then we say "we have insufficient evidence to reject H0".
|
We will work our way through an example to see this.
Assume that we have a population of values
and that the standard deviation of those values in the population
is σ=15.
I claim that the mean of the population, μ is equal to 134.
You do not believe me.
You think the mean of the population is not equal to 134.
Notice that you are not saying what the true mean is, just that
it is not 134.
It is hard for you to tell me that I am wrong, so you decide that
you will take a sample of the population, compute the sample mean, and
examine just how strange that sample mean is.
You happen to know that sample means from samples of size 36 from
a population with a standard deviation σ = 15 will
be approximately normally distributed with
the standard deviation of the sample mean
equal to σ / √36 or in our case, 15 / 6 = 2.5.
Clearly, if you get a sample mean of 200, you are going to
tell me that I am completely wrong.
The value 200 is over 20 standard deviations above the
value 134, the value we would expect to get if the true mean is 134.
Random sampling is just not going to produce that kind of rare event.
Well, it could happen, but the odds against it are so great you just say it is
too unlikely to happen and reject my hypothesis.
On the other hand, if the sample mean turns out to be 134.7 then
you would never think that getting such a sample mean
would justify your claim that I am wrong.
You have seen many examples where the sample mean
changes with each sample and where the value of the sample mean is often
more than one standard deviation
away from the true population mean.
In fact, you recall that about 68% of the values
in a normally distributed
population are within 1 standard deviation of the mean.
That means that about 32%
of the values are more than 1 standard deviation away from the mean.
We would expect that nearly 1/3 of the
time a sample of 36 items taken from
our population (which we know has σ=15 so
sx=2.5) will have values that are
more than 2.5 above or below the true mean.
If the true mean is 134 then getting
a 36-item sample mean of that population that
is 0.7 or more above or below 134 should
happen really often (in fact, nearly 48.4% of the time).
If we are using the critical value approach,
the question becomes, at what point is the sample mean far enough away
from the supposed 134 for you to say that getting such a sample mean is just too
unlikely; for you to risk claiming that my 134 value
cannot be right because if it were then it is just too unlikely
that you would get a 36-item random sample with such an extremely
different sample mean.
You answer that question by using the level of significance
that you specify. If you are only willing to make a Type I error
1% of the time, then you want to find a value for the sample mean
that is so extreme that only 1% of the normal distribution
of 36-item sample means will be that or more extremely different from
my hypothesis value of 134.
For this example, an extreme value can be too high or too low.
You need to split the 1% error that you are willing to make
between these two options.
You know (from the tables, a calculator, or qnorm() )
that less than 0.5% (0.005 square units) of the area under
the standard normal curve
is less than the z-score = -2.58 [and, correspondingly, less than 0.5%
of the area under the standard normal curve is greater than 2.58].
Therefore, you know that being more than 2.58 standard deviations above or below
the true population mean
will happen less than 1% of the time. But you know that the
sample means have a standard deviation of 2.5. Therefore,
for this problem, you know that getting a sample mean that is more than
2.58*2.5 = 6.45 away from the true population mean will
happen less than 1% of the time.
You conclude that, assuming I am correct about μ=134, then getting a
36-item sample mean that is less than 134-6.45 = 127.55 or
that is greater than
134+6.45 = 140.45 will happen less than 1% of the time.
Therefore, if the sample mean turns out to be less than or equal to
127.55 or greater than or equal to 140.45 you will feel
absolutely justified in claiming that I am wrong.
If, when you take a sample, you get a sample mean that is more
extreme than those critical values then
you would say that I am wrong,
you would reject H0: μ = 134
in favor of the alternative
H1: μ ≠ 134,
all the while knowing that there is a
really small chance that the true mean really was 134.
Now you take your sample. The values of that sample are shown in
Table 1.
The computations that we did above are pretty straight forward.
We could do them, excluding finding the sample mean,
with a bit more accuracy, in R
using:
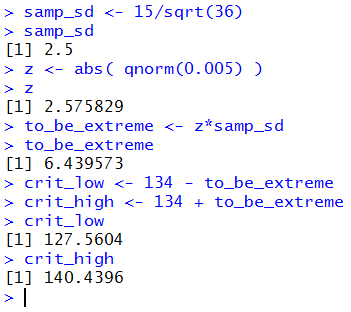
samp_sd <- 15/sqrt(36)
samp_sd
z <- abs( qnorm(0.005) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_low <- 134 - to_be_extreme
crit_high <- 134 + to_be_extreme
crit_low
crit_high
|
Sorry, but I cannot show the R computation
for the mean of the values in Table 1
because the reproductions of the R screens are static
whereas the values in the table change
whenever the page is refreshed.
It should be enough, at this point in the course, to say
that if you use the gnrnd4() command as given above, then the data will be in
L1 and you can get the mean of those values with the command mean(L1).
|
Figure 1 shows making those computations in R.
Figure 1
The last part of the presentation above walked us through the critical value approach.
You could use the attained significance approach instead.
To do that, after determining that you are willing to
make a Type I error 1% of the time,
you take your 36-item sample.
You already have that back in Table 1.
Then you compute the sample mean for that data, and you have that above,
namely,
. Following that you look to see just
how likely it is to get a value that extreme or more extreme
assuming that H0 is true, that the true population mean is 134.
You know that the standard deviation of the population is 15,
and you know the distribution of the means 36-item samples will have
a mean of 134 and a standard deviation of 15/sqrt(36).
Another example follows, this time with a bit less dialogue.
We have a population which we
know to be approximately normal.
We also know that the population standard deviation
is σ = 3.
There is a claim, a hypothesis, that the population mean is
μ = 14.2, but we believe, for whatever reason, that
the true population mean is higher than that.
We want to test H0: μ = 14.2
against the alternative
H1: μ > 14.2 at
the 0.05 level of significance,
meaning we are willing to make a Type I
error one out of twenty times.
This is a "one-sided test" because the only time we will
reject H0 is if we get a sample mean significantly greater
than the H0 value of 14.2.
We find (via the table, the calculator,
or the computer) that the z-score with 0.05
area above it [which we know is the opposite
of the z-score with 0.05 below it] is
about 1.64485.
Because the population is normal we can get
away with a smaller sample size. In fact,
we decide to use a sample of size n=17.
That means that the distribution of 17-item sample means will be
approximately normal with standard deviation equal to approximately 3/sqrt(17)
or about 3/4.123 ≈ 0.7276.
Thus, to be "really extreme" our sample mean
would have to be greater than or equal to
14.2 + 1.64485*0.7276 ≈ 14.2 + 1.1968 = 15.3968.
That means that our one and only critical value is 15.3968.
We take a sample, the values of which are shown in Table 2.
The computations that we did above are pretty straight forward.
We could do them, excluding finding the sample mean,
with a bit more accuracy, in R
using:
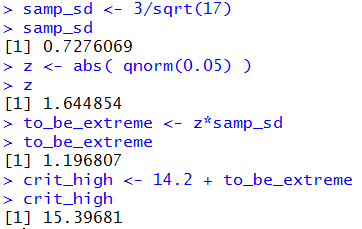
samp_sd <- 3/sqrt(17)
samp_sd
z <- abs( qnorm(0.05) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_high <- 14.2 + to_be_extreme
crit_high
Figure 2 shows making those computations in R.
Figure 2
To do this same problem using the attained significance approach
we would ask "What is the probability that if H0 is true
we would find a random sample of 17 items with a sample mean that is
Here is a third example, one given with even less discussion.
We have a population and a null hypothesis
H0: μ = 239.7
with the alternative hypothesis
H1: μ < 239.7.
We want to test H0 at the
0.035 level of significance.
We know the population standard deviation,
σ = 43.6.
There is a real concern that the population is not normally distributed.
To address that concern we choose a sample size greater than 30.
Our sample size will be n=68.
For the critical value approach, we note that
the standard deviation of sample means in
samples of size 68 will be σ/sqrt(68) ≈ 43.6/8.2462 ≈ 5.2873.
The z-score with the area 0.035 to its left is
about -1.812. Our critical value will be
the single value 239.7+(-1.812*5.2873) ≈ 239.7 - 9.581 ≈ 230.12.
We take a random sample of 68 items. The values are reported in Table 3.
We could do those computations, excluding finding the sample mean,
with a bit more accuracy, in R
using:
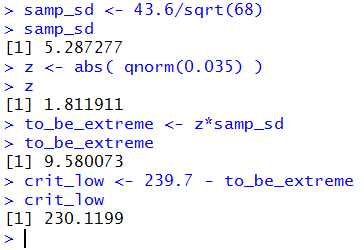
samp_sd <- 43.6/sqrt(68)
samp_sd
z <- abs( qnorm(0.035) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_low <- 239.7 - to_be_extreme
crit_low
Figure 3 shows making those computations in R.
Figure 3
To do this same problem using the attained significance approach
we would ask "What is the probability that if H0 is true
we would find a random sample of 68 items with a sample mean that is
The three dynamic (the samples change each time the page is reloaded or refreshed)
examples above walk through problems of testing
the null hypothesis for the population,
where we know the population standard deviation,
by drawing a sample and using either the critical value
or the attained significance approach.
In that "walking through" the problems we begin to recognize that
the steps we will take are almost identical for each problem.
We should be able to capture those steps in some R function.
Consider the following function (available in the file
hypo_known.R):
hypoth_test_known <- function(
H0_mu, sigma, H1_type=0, sig_level=0.05,
samp_size, samp_mean)
{ # perform a hypothesis test for the mean=H0_mu
# when we know sigma and the alternative hypothesis is
# != if H1_type==0
# < if H1_type < 0
# > if H1_type > 0
# Do the test at sig_level significance, for a
# sample of size samp_size that yields a sample
# mean = samp_mean.
samp_sd <- sigma/sqrt(samp_size)
if( H1_type==0)
{ z <- abs( qnorm(sig_level/2))}
else
{ z <- abs( qnorm(sig_level))}
to_be_extreme <- z*samp_sd
decision <- "Reject"
if( H1_type < 0 )
{ crit_low <- H0_mu - to_be_extreme
crit_high = "n.a."
if( samp_mean > crit_low)
{ decision <- "do not reject"}
attained <- pnorm( samp_mean, H0_mu, samp_sd)
alt <- paste("mu < ", H0_mu)
}
else if ( H1_type == 0)
{ crit_low <- H0_mu - to_be_extreme
crit_high <- H0_mu + to_be_extreme
if( (crit_low < samp_mean) & (samp_mean < crit_high) )
{ decision <- "do not reject"}
if( samp_mean < H0_mu )
{ attained <- 2*pnorm(samp_mean, H0_mu, samp_sd)}
else
{ attained <- 2*pnorm(samp_mean, H0_mu, samp_sd,
lower.tail=FALSE)
}
alt <- paste( "mu != ", H0_mu)
}
else
{ crit_low <- "n.a."
crit_high <- H0_mu + to_be_extreme
if( samp_mean < crit_high)
{ decision <- "do not reject"}
attained <- pnorm(samp_mean, H0_mu, samp_sd,
lower.tail=FALSE)
alt <- paste("mu > ",H0_mu)
}
z <- (samp_mean - H0_mu)/samp_sd
result <- c(H0_mu, alt, sigma, samp_size, sig_level,
samp_mean, samp_sd, to_be_extreme, z,
crit_low, crit_high, attained, decision)
names(result) <- c("H0_mu", "H1:", "sigma", "n",
"sig level", "samp mean",
"sd samp mean", "how far", "test stat",
"critical low", "critical high",
"attained", "decision")
return( result)
}
This is a long function, but it is really just the steps that we
have taken in the previous examples. One of the things that make the
function so long is that we have to build into it all of
the "logic" that we apply to the problems as we do them. Thus, we had to build in
the idea of splitting the significance level
between both high and low values for the alternative hypothesis of being
"not equal to". We also wanted to build in the process of deciding if we want to reject or not reject
the null hypothesis.
As much as I would like to demonstrate how this function works for the
examples above, I cannot do that here since those examples
each contained random samples that change every time you load the page.
However, I can repeat each of the cases with a fixed random sample that
I have taken, and which will be shown below, and then I can use the function to
solve that fixed problem.
Revisit Example 1:
Recall that we had H0: μ = 134,
H1: μ ≠ 134
σ=15, and the significance level was 0.01.
We decided to take a 36-item sample.
Then we found that the two critical values were
127.55 and 140.45. Then we take a sample.
For this report the sample taken is now given in Table 4.
The computations, other than getting the sample mean, are exactly those shown in Figure 1
above. But now, since this is a static example, we can show not only generating the data and
getting the sample mean, but also getting the attained significance.
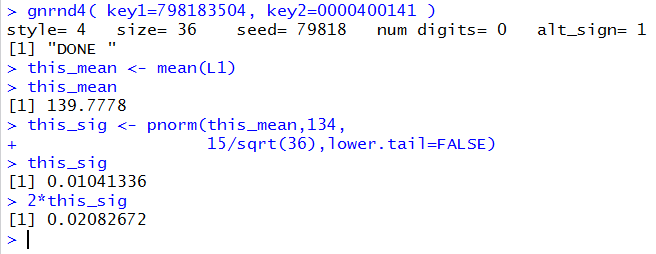
The R commands are
gnrnd4( key1=798183504, key2=0000400141 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,134,
15/sqrt(36),lower.tail=FALSE)
this_sig
2*this_sig
Figure 4
Rather than do all of that work, we could just use our function.
The command would be
hypoth_test_known(134, 15, 0, 0.01, 36, 139.778 )
The third argument is set to 0
because the alternative hypothesis is a case of not equal.
Figure 5

The response to the function statement is a long list of
values. That list includes all of the values sent to the function as well as
almost all of the values computed by the function. We can find,
as part of the results shown in Figure 5,
almost anything that we want, including the decision that
needs to be made for this case.
|
Note that the function output includes the test statistic
which is the standardized version of the sample mean.
|
Revisit Example 2:
Recall that we had population that is N(μ,3) and
H0: μ = 14.2
against the alternative
H0: μ > 14.2.
We want to test H0 at the
0.05 level of significance. We will do this with a sample of size
n=17. We can compute the standard deviation of
the means of repeated samples of size 17 to be 3/sqrt(17)
which we approximate as 0.7276. The z-score that we will use
to have an area of 0.05 to its right we found to be
about 1.64485, which gives rise to our
saying that the sole critical value for this problem will be
15.3968. We take our sample, shown in Table 5.
The computations, other than getting the sample mean,
are exactly those shown in Figure 2
above. But now, since this is a static example,
we can show not only generating the data and
getting the sample mean, but also getting the attained significance.
The R commands are
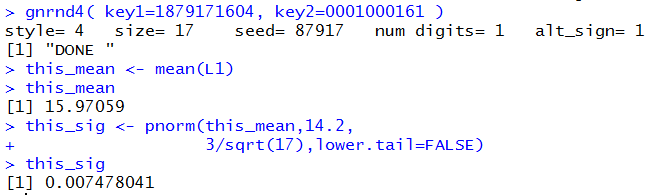
gnrnd4( key1=1879171604, key2=0001000161 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,14.2,
3/sqrt(17),lower.tail=FALSE)
this_sig
The console view of these commands is shown in Figure 6.
Figure 6
Rather than do all of that work, we could just use our function.
The command would be
hypoth_test_known(14.2, 3, 1, 0.01, 17, 15.971 )
The third argument is set to 1, a positive value,
because the alternative hypothesis is a case of "is greater than".
Figure 7

As expected, all of the values we need are part of the
output of the function statement.
|
Note that the function output includes the test statistic
which is the standardized version of the sample mean.
|
Revisit Example 3:
Recall that we had a population with σ=43.6 and hypotheses
H0: μ = 239.7 with
H1: μ < 239.7.
We want to test H0 at the
0.035 level of significance.
We decide to use a sample of size n=68.
This gives us the value 5.2873 as the standard deviation of the means of repeated
samples of size 68. The z-score with the area 0.035 to its left
was -1.812.
As a result, we computed the sole critical value
to be about 230.12.
The we take our sample, shown in Table 6 and we find its mean.
The computations, other than getting the sample mean,
are exactly those shown in Figure 3
above. But now, since this is a static example,
we can show not only generating the data and
getting the sample mean, but also getting the attained significance.
The R commands are
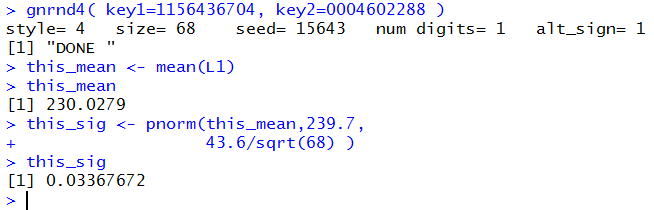
gnrnd4( key1=1156436704, key2=0004602288 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,239.7,
43.6/sqrt(68) )
this_sig
The console view of these commands is shown in Figure 8.
Figure 8
Rather than do all of that work, we could just use our function.
The command would be
hypoth_test_known(239.7, 43.6, -1, 0.035, 68, 230.028 )
The third argument is set to -1, a negative value,
because the alternative hypothesis is a case of "is less than".
This command is shown in Figure 9.
Figure 9

As expected, all of the values we need are part of the
output of the function statement.
|
Note that the function output includes the test statistic
which is the standardized version of the sample mean.
|
Below is a listing of the R commands used in generating this page.
samp_sd <- 15/sqrt(36)
samp_sd
z <- abs( qnorm(0.005) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_low <- 134 - to_be_extreme
crit_high <- 134 + to_be_extreme
crit_low
crit_high
samp_sd <- 3/sqrt(17)
samp_sd
z <- abs( qnorm(0.05) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_high <- 14.2 + to_be_extreme
crit_high
samp_sd <- 43.6/sqrt(68)
samp_sd
z <- abs( qnorm(0.035) )
z
to_be_extreme <- z*samp_sd
to_be_extreme
crit_low <- 239.7 - to_be_extreme
crit_low
source("../hypo_known.R")
gnrnd4( key1=798183504, key2=0000400141 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,134,
15/sqrt(36),lower.tail=FALSE)
this_sig
2*this_sig
hypoth_test_known(134, 15, 0, 0.01, 36, 139.778 )
gnrnd4( key1=1879171604, key2=0001000161 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,14.2,
3/sqrt(17),lower.tail=FALSE)
this_sig
hypoth_test_known(14.2, 3, 1, 0.01, 17, 15.971 )
gnrnd4( key1=1156436704, key2=0004602288 )
this_mean <- mean(L1)
this_mean
this_sig <- pnorm(this_mean,239.7,
43.6/sqrt(68) )
this_sig
hypoth_test_known(239.7, 43.6, -1, 0.035, 68, 230.028 )
Return to Topics page
©Roger M. Palay
Saline, MI 48176 March, 2025
 .
.
 is more extreme than the critical value(s)
then we say that
"we reject H0 in favor of
the alternate H1". If the
sample mean
is not more extreme than the critical value(s)
then we say "we have insufficient evidence to reject H0".
is more extreme than the critical value(s)
then we say that
"we reject H0 in favor of
the alternate H1". If the
sample mean
is not more extreme than the critical value(s)
then we say "we have insufficient evidence to reject H0".
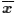 .
.
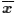 or a value more extreme than that.
We can do this using the fact that the distribution of
sample means for samples of size n is normal
with mean=μ and standard deviation=σ/sqrt(n).
or a value more extreme than that.
We can do this using the fact that the distribution of
sample means for samples of size n is normal
with mean=μ and standard deviation=σ/sqrt(n).








